- Як обчислити площу куба
- Інструкція
- Зверніть увагу
- Корисні поради
- Формули площі поверхні геометричних фігур.
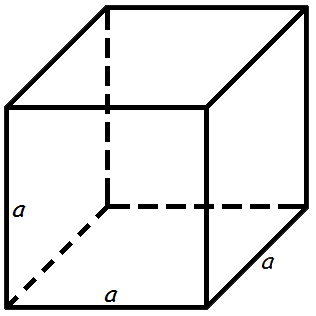
- Площа куба
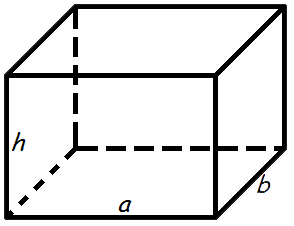
- Площа прямокутного паралелепіпеда
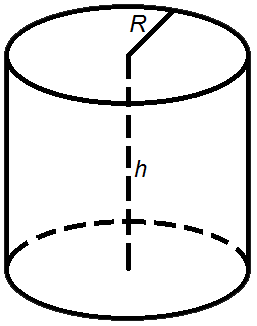
- Площа циліндра
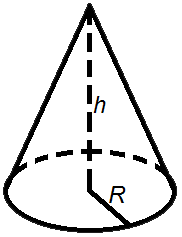
- Площа конуса
- Площа кулі
- Як обчислити площу куба
- Площадь поверхности куба.
- Определение площади поверхности куба.
- Чему равна площадь поверхности куба.
- Як знайти площу куба
- Кроки
- Метод 1 з 2: Якщо ви знаєте довжину однієї зі сторін
- Метод 2 з 2: Якщо дана тільки обсяг
- Як обчислити площу куба
- Трохи інформації про кубі і про способи того, як обчислити площу поверхні куба
- Що таке площа?
- Яка фігура називається кубом?
- Як пов`язаний куб з іншими фігурами і тілами?
- Метод 1: обчислення площі куба по його ребру
- Метод 2: як обчислити площу, якщо відомий обсяг тіла
- Метод 3: розрахунок площі по діагоналі куба
- Метод 4: як скористатися радіусом вписаного або описаного кола для обчислення площі куба
- Кілька слів про бічній поверхні гексаедр
- приклади завдань
Як обчислити площу куба
Куб являє собою окремий випадок паралелепіпеда, в якому кожна з граней утворена правильним багатокутником — квадратом. Усього куб володіє шістьма гранями. Обчислити площу не становить труднощів.
Інструкція
- Спочатку необхідно обчислити площу кожного з квадратів, який є межею даного куба. Площа квадрата можна обчислити, перемноживши один на одного пару з його сторін. Формулою це можна виразити так:
S = a * a = a ²
Тепер, знаючи площа однієї з грані квадрата, можна дізнатися площа всієї поверхні куба. Це можна здійснити, якщо модифіковані формулу, вказану вище:
Інакше кажучи, знаючи, що таких квадратів (граней) у куба аж шість штук, то площа поверхні куба становить площ однією з граней куба.
Для наочності і зручності можна привести приклад:
Припустимо, даний куб, у якого довжина ребра дорівнює 6 см, потрібно знайти площу поверхні даного куба. Спочатку потрібно знайти площу грані:
Таким чином, дізнавшись площа грані, можна знайти і всю площі поверхні куба:
Відповідь: площа поверхні куба з ребром, рівним 6 см, становить 216 см ²
Зверніть увагу
Куб є окремим випадком не тільки паралелепіпеда, але і призми.
Паралелепіпедом називається призма, у якого підставою є паралелограм. Особливістю паралелепіпеда є те, що 4 з 6 його граней — прямокутники.
Корисні поради
Якщо даний не куб, а інший правильний багатогранник, то в будь-якому випадку, площа його поверхні буде перебувати аналогічно. Це означає, що площа поверхні правильного багатогранника знаходиться шляхом підсумовування всіх площ його граней — правильних багатокутників.
Формули площі поверхні геометричних фігур.
Площа куба
Площа поверхні куба дорівнює квадрату довжини його грані помноженому на шість.
Площа прямокутного паралелепіпеда
Площа циліндра
Площа бокової поверхні круглого циліндра дорівнює добутку периметру його основи на висоту.
Формула для обчислення площі бокової поверхні циліндра:
Площа повної поверхні круглого циліндра дорівнює сумі площ бокової поверхні циліндра та подвоєної площі основи.
Формула для обчислення площі повної поверхні циліндра:
Площа конуса
Площа бокової поверхні конуса дорівнює добутку його радіуса і твірної помноженому на число π .
Формула площі бокової поверхні конуса:
Площа повної поверхні конуса дорівнює сумі площ основи конуса і площі бокової поверхні.
Формула площі повної поверхні конуса:
Площа кулі
Площа поверхні кулі дорівнює чотирьом його радіусам в квадраті, помножених на число π .
Площа поверхні кулі дорівнює квадрату його діаметру помноженому на число π .
Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!
Вітаю всіх користувачів OnlineMSchool.
Мене звати Довжик Михайло Вікторович. Я власник і автор цього сайту, мною написано весь теоретичний матеріал, а також розроблені онлайн вправи та калькулятори, якими Ви можете скористатися для вивчення математики.
Як обчислити площу куба
При спадкуванні за законом якщо спадкове майно переходить до двох або декількох спадкоємців, і при…
Закохана жінка прекрасна — її обличчя одухотворене, очі сяють, а з обличчя не сходить лукава…
Образи дисків є їх повними копіями, представленими у вигляді файлу. Як правило, зберігається в…
Якщо ваш мобільний комп’ютер періодично відключається, необхідно з’ясувати причину цього процесу.…
Портативні рації використовуються в багатьох аспектах активного життя. Вони не потребують…
Вогонь необхідний людині в лісі. Якщо у вас буде розпалене багаття, ви завжди зможете висушити…
Будь правильний багатокутник можна вписати в коло. Тому при побудові правильного восьмикутника…
Бувають ситуації, коли користувач випадково видаляє будь-які потрібні файли або папки зі свого…
В костюмі і при краватці ви виглядаєте дуже навіть нічого. Широкі плечі, рівна спина, прямі ноги,…
Площадь поверхности куба.
Площадь поверхности куба – это суммарная площадь всех поверхностей фигуры. Площадь поверхности куба равна сумме площадей всех его шести граней. Площадь поверхности является числовой характеристикой поверхности. Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.
Определение площади поверхности куба.
Определение площади поверхности куба выполняется по формуле SA = 6а 2 . Куб (правильный гексаэдр) — это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.
Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а 2 . Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять — a 2 , где а – сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а – ребро куба (сторона квадрата).
Чему равна площадь поверхности куба.
Площадь поверхности куба измеряется в квадратных единицах, к примеру, в мм 2 , см 2 , м 2 и так далее. Для дальнейших расчетов Вам необходимо будет измерить ребро куба. Как мы знаем, ребра у куба равны, поэтому Вам будет достаточно измерить только одно (любое) ребро куба. Выполнить такой замер Вы можете при помощи линейки (или рулетки). Обратите внимание на единицы измерения на линейке или рулетке и запишите значение, обозначив его через а.
Полученное значение возведите в квадрат. Таким образом, Вы возведите в квадрат длину ребра куба. Для того чтобы возвести число в квадрат умножьте его на себя. Наша формула будет иметь следующий вид: SA = 6*а 2
Вы вычислили значение площади одной из граней куба.
Полученное значение умножайте на шесть. Не забывайте, что у куба 6 равных граней. Определив площадь одной из граней, умножьте полученное значение на 6, чтобы все грани куба участвовали в расчете.
Вот мы и пришли к конечному действию по вычислению площади поверхности куба.
Як знайти площу куба
Площа куба — це сума площі всіх його сторін. Всі сторони куба рівні, тому, щоб знайти площу куба, треба знайти площу однієї з його сторін і помножити на 6. Ми розповімо, як це робиться.
Кроки
Метод 1 з 2: Якщо ви знаєте довжину однієї зі сторін
Площа куба — це сума площі всіх шести його сторін. Ось формула: 6 xs, де «s» це сторона куба.
Знайдіть площу однієї зі сторін куба, тобто «s», довжину сторони куба, а потім потрібно знайти s. Тобто, довжина сторони куба в квадраті — це площа, оскільки довжина і ширина рівні між собою. Якщо одна сторона куба, «s», дорівнює 4 см, тоді площа сторони куба дорівнює (4 см), тобто 16 см. Площа завжди записується в см квадратних.
Помножте площа сторони куба на 6. 16 см x 6 = 96 см. Площа куба дорівнює 96 см.
Метод 2 з 2: Якщо дана тільки обсяг
Знайдіть об`єм куба. Наприклад, обсяг куба 125 см.
Знайдіть корінь кубічний обсягу куба. У нашому випадку кубічний корінь числа 125 це 5, тому що 5 x 5 x 5 = 125. У нашому випадку, «s», тобто одна сторона куба дорівнює 5.
Підставте цей результат в формулу площі куба: 6 x s. Довжина однієї сторони куба 5 см, значить: 6 x (5 см).
Вирішіть приклад. 6 x (5 см) = 6 x 25 см = 150 см.
Як обчислити площу куба
При спадкуванні за законом якщо спадкове майно переходить до двох або декількох спадкоємців, і при…
Закохана жінка прекрасна — її обличчя одухотворене, очі сяють, а з обличчя не сходить лукава…
Образи дисків є їх повними копіями, представленими у вигляді файлу. Як правило, зберігається в…
Якщо ваш мобільний комп’ютер періодично відключається, необхідно з’ясувати причину цього процесу.…
Портативні рації використовуються в багатьох аспектах активного життя. Вони не потребують…
Вогонь необхідний людині в лісі. Якщо у вас буде розпалене багаття, ви завжди зможете висушити…
Будь правильний багатокутник можна вписати в коло. Тому при побудові правильного восьмикутника…
Бувають ситуації, коли користувач випадково видаляє будь-які потрібні файли або папки зі свого…
В костюмі і при краватці ви виглядаєте дуже навіть нічого. Широкі плечі, рівна спина, прямі ноги,…
Трохи інформації про кубі і про способи того, як обчислити площу поверхні куба
Куб — дивовижна фігура. Він однаковий з усіх боків. Будь-яка його грань може вмить стати підставою або бічній. І від цього нічого не зміниться. А формули для нього завжди легко запам`ятовуються. І неважливо, що потрібно знайти — обсяг або площа поверхні куба. В останньому випадку навіть не потрібно вчити щось нове. Досить пам`ятати тільки формулу площі квадрата.
Що таке площа?
Цю величину прийнято позначати латинською буквою S. Причому це справедливо для шкільних предметів, таких як фізика і математика. Вимірюється вона в квадратних одиницях довжини. Все залежить від даних в задачі величин. Це можуть бути мм, см, м або км в квадраті. Причому можливі випадки, коли одиниці навіть не вказані. Йдеться просто про числовому вираженні площі без назви.
Так що ж таке площа? Це величина, яка є числовою характеристикою розглянутої фігури або об`ємного тіла. Вона показує розмір її поверхні, яка обмежена сторонами фігури.
Яка фігура називається кубом?
Ця фігура є многогранником. Причому непростим. Він правильний, тобто у нього всі елементи дорівнюють один одному. Будь то сторони або грані. Кожна поверхня куба являє собою квадрат.
Інша назва куба — правильний гексаедр, якщо по-російськи, то шестигранник. Він може бути утворений з чотирикутної призми або паралелепіпеда. При дотриманні умови, коли всі ребра рівні і кути утворюють 90 градусів.
Ця фігура настільки гармонійна, що часто використовується в побуті. Наприклад, перші іграшки малюка — кубики. А забава для тих, хто постарше, — кубик Рубика.
Як пов`язаний куб з іншими фігурами і тілами?
Якщо накреслити перетин куба, яке проходить через три його межі, то воно матиме вид трикутника. У міру віддалення від вершини перетин буде все більше. Настане момент, коли перетинатися будуть вже 4 грані, і фігура в перерізі стане чотирикутником. Якщо провести розтин через центр куба так, щоб воно було перпендикулярно його головним діагоналях, то вийде правильний шестикутник.
Усередині куба можна накреслити тетраедр (трикутну піраміду). За вершину тетраедра береться один з його кутів. Решта три співпадуть з вершинами, які лежать на протилежних кінцях ребер обраного кута куба.
У нього можна вписати октаедр (опуклий правильний багатогранник, який схожий на дві з`єднані піраміди). Для цього потрібно знайти центри всіх граней куба. Вони будуть вершинами октаедра.
Можлива і зворотна операція, тобто всередину октаедра реально вписати куб. Тільки тепер центри граней першого стануть вершинами для другого.
Метод 1: обчислення площі куба по його ребру
Для того щоб обчислити всю площу поверхні куба, потрібно знання одного з його елементів. Найпростіший спосіб вирішення, коли відомо його ребро або, іншими словами, сторона квадрата, з якого він складається. Зазвичай ця величина позначається латинською буквою «а».
Тепер потрібно згадати формулу, по якій обчислюється площа квадрата. Щоб не заплутатися, введено її позначення буквою S1.
Для зручності краще задати номери всім формулами. Ця буде першою.
Але це площа тільки одного квадратика. Всього їх шість: 4 з боків і 2 знизу і зверху. Тоді площа поверхні куба обчислюється за такою формулою: S = 6 * a 2 . Її номер 2.
Метод 2: як обчислити площу, якщо відомий обсяг тіла
Цей спосіб зводиться до того, щоб порахувати довжину ребра за відомим об`ємом. І потім вже скористатися відомою формулою, яка тут позначена цифрою 2.
З математичного виразу для обсягу гексаедр виводиться то, за яким можна порахувати довжину ребра. Ось вона:
Нумерація триває, і тут уже цифра 3.
Тепер його можна обчислити і підставити в другу формулу. Якщо діяти за нормами математики, то потрібно вивести такий вислів:
Це формула площі всієї поверхні куба, якою можна скористатися, якщо відомий обсяг. Номер цього запису 4.
Метод 3: розрахунок площі по діагоналі куба
Для того щоб розрахувати площа повної поверхні куба, також буде потрібно вивести ребро через відому діагональ. Тут використовується формула для головної діагоналі гексаедр:
З неї легко вивести вираз для ребра куба:
Це шоста формула. Після його обчислення можна знову скористатися формулою під другим номером. Але краще записати таку:
Вона виявляється пронумерованій цифрою 7. Якщо уважно подивитися, то можна помітити, що остання формула зручніше, ніж поетапний розрахунок.
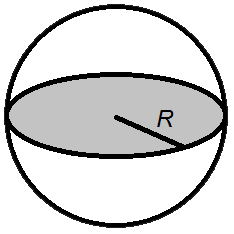
Метод 4: як скористатися радіусом вписаного або описаного кола для обчислення площі куба
Якщо позначити радіус описаного навколо гексаедр окружності буквою R, то площа поверхні куба буде легко обчислити за такою формулою:
Її порядковий номер 8. Вона легко виходить завдяки тому, що діаметр окружності повністю збігається з головною діагоналлю.
Позначивши радіус вписаного кола латинською буквою r, можна отримати таку формулу для площі всієї поверхні гексаедр:
Кілька слів про бічній поверхні гексаедр
Якщо в задачі потрібно знайти площу бічної поверхні куба, то потрібно скористатися вже описаним вище прийомом. Коли вже дано ребро тіла, то просто площа квадрата потрібно помножити на 4. Ця цифра з`явилася через те, що бічних граней у куба всього 4. Математична запис цього виразу така:
Її номер 10. Якщо дані якісь інші величини, то надходять аналогічно описаним вище методам.
приклади завдань
Умова першої. Відома площа поверхні куба. Вона дорівнює 200 смsup2-. Необхідно обчислити головну діагональ куба.
1 спосіб. Потрібно скористатися формулою, яка позначена цифрою 2. З неї буде нескладно вивести «а». Ця математична запис буде виглядати як квадратний корінь з приватного, рівного S на 6. Після підстановки чисел виходить:
а = radic- (200/6) = radic- (100/3) = 10 radic-3 (див).
П`ята формула дозволяє відразу обчислити головну діагональ куба. Для цього потрібно значення ребра помножити на radic-3. Це просто. У відповіді виходить, що діагональ дорівнює 10 см.
2 спосіб. На випадок якщо забулася формула для діагоналі, але пам`ятається теорема Піфагора.
Аналогічно тому, як було в першому способі, знайти ребро. Потім потрібно записати теорему для гіпотенузи два рази: першу для трикутника на межі, другу для того, який містить шукану діагональ.
хsup2- = аsup2- + аsup2-, де х — діагональ квадрата.
dsup2- = хsup2- + аsup2- = аsup2- + аsup2- + аsup2- = 3 аsup2-. З цього запису легко видно, як виходить формула для діагоналі. А далі всі розрахунки будуть, як в першому способі. Він трошки довше, але дозволяє не запам`ятовувати формулу, а отримати її самостійно.
Відповідь: діагональ куба дорівнює 10 см.
Умова другий. За відомою площі поверхні, яка дорівнює 54 см 2 , обчислити об`єм куба.
Користуючись формулою під другим номером, потрібно дізнатися значення ребра куба. Те, як це робиться, докладно описано в першому способі рішення попередньої задачі. Провівши все обчислення, отримаємо, що а = 3 см.
Тепер потрібно скористатися формулою для обсягу куба, в якій довжина ребра зводиться в третю ступінь. Значить, обсяг буде вважатися так: V = 3 3 = 27 см 3 .
Відповідь: обсяг куба дорівнює 27 см 3 .
Умова третьої. Потрібно знайти ребро куба, для якого виконується така умова. При збільшенні ребра на 9 одиниць площа всієї поверхні збільшується на 594.
Оскільки явних чисел в завданню не дано, тільки різниці між тим, що було, і тим, що стало, то потрібно ввести додаткові позначення. Це не складно. Нехай шукана величина буде дорівнює «а». Тоді збільшене ребро куба дорівнюватиме (а + 9).
Знаючи це, потрібно записати формулу для площі поверхні куба два рази. Перша — для початкового значення ребра — співпаде з тією, яка пронумерована цифрою 2. Друга буде трохи відрізнятися. У ній замість «а» потрібно записати суму (а + 9). Так як в завданні йдеться про різниці площ, то потрібно відняти з більшої площі меншу:
Потрібно провести перетворення. Спочатку винести за дужки 6 в лівій частині рівності, а потім спростити те, що залишиться в дужках. А саме (а + 9) 2 — а 2 . Тут записана різниця квадратів, яку можна перетворити так: (а + 9 — а) (а + 9 + а). Після спрощення виразу виходить 9 (2а + 9).
Тепер його потрібно помножити на 6, тобто те число, що було перед дужкою, і прирівняти до 594: 54 (2а + 9) = 594. Це лінійне рівняння з однієї невідомої. Його легко вирішити. Спочатку потрібно розкрити дужки, а потім перенести в ліву частину рівності доданок з невідомою величиною, а числа — в праву. Вийде рівняння: 2а = 2. З нього видно, що шукана величина дорівнює 1.