Все грани куба окрашены найти вероятность того что

Задача 23687 Куб, все грани которого окрашены.

Условие

Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем одинаково перемешаны. Найти вероятность того, что на удачу извлечённый кубик имеет:

1) 1 окрашенную грань;
2) 2 окрашенные грани
3) 3 окрашенные грани

Решение

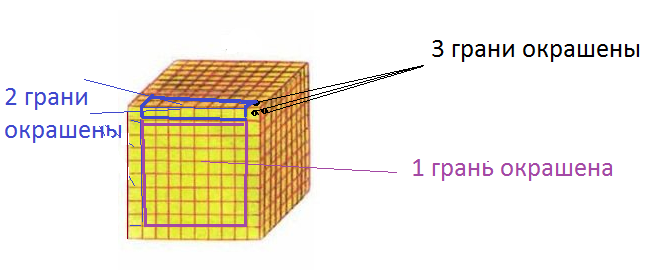
У куба 6 граней. На каждой грани расположено 10*10=100 квадратов, которые являются основаниями маленьких кубиков.

С тремя окрашенными гранями 8 кубиков , они расположены в 8-ми вершинах куба.

Кубики, имеющие 2 окрашенные грани, находятся на ребрах куба и не совпадают с вершинами.
На одном ребре куба находится 10 кубиков.
2 кубика в углах — вершины, они имеют по три окрашенные грани, значит
10-2=8 кубиков имеют по две окрашенные грани.
У куба 12 ребер, следовательно, всего таких кубиков 12*8=96 штук.

Одну окрашенную грань имеют кубики, которые лежат на грани, но не лежат на ребре.

Таких кубиков на одной грани 100- 8*4-4=64

На 6 гранях лежат 64*6= 384 кубика с одной окрашенной гранью.

По формуле классической вероятности
1) р=384/1000=0,384 вероятность того, что на удачу извлечённый кубик имеет 1 окрашенную грань;
2) p=96/1000=0,096 вероятность того, что на удачу извлечённый кубик имеет 2 окрашенные грани;
3) р=8/1000 = 0,008 вероятность того, что на удачу извлечённый кубик имеет 3 окрашенные грани.

О т в е т.
1) 0,384;
2)0,096;
3)0,008

Между прочим, кубиков с неокрашенными гранями
1000-384-96-8=512

Источник

Вероятность взять кубик с окрашенными гранями.

Кубик рубик с разными гранями
Купил кубик рубик с разными гранями. Не могли бы подсказать как его собрать. Алгоритмы сборки.

Найти вероятность того, что извлеченные из ящика детали окажутся окрашенными.
1)В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали.

Какова вероятность того, что среди извлеченных деталей 3 будут окрашенными?
В ящике 15 деталей, среди которых 12 окрашенных. Сборщик наугад извлекает 5 деталей. Какова.

Найти вероятность того, что среди извлеченных деталей первая и последняя детали окажутся окрашенными
1, В ящике 10 деталей, среди которых шесть окрашенных. Сборщик наудачу извлекает четыре.

это чтобы вы представили:
распилили, получили 10*10*10 кубиков
с) количество вершин куба 8, отсюда 8 покрашенных граней;
б) вершины исключили и на ребрах(12 штук) по 8 кубиков(потому что два уже посчитаны ранее): 8*12=96;
а) вершины исключили и ребра тоже, получается 6 граней количеством 8*8(64): 6*64=384.

Задача на условную вероятность про игральные кости с цветными гранями
Игральная кость A имеет две красных и четыре белых грани, кость B — три красных и три белых, кость.

Задача про игральный кубик — найти вероятность события
Добрый день, форумчане. Помогите пожалуйста, кому не безразлично, решить такую задачу:

Игральный кубик подбрасывают 6 раз. Найти вероятность того, что “5” выпадет
Игральный кубик подбрасывают 6 раз. Найти вероятность того, что “5” выпадет: а) один раз; б) хотя.

Найти вероятность того, что кубик придётся кидать четвёртый раз
Игральный кубик подкидывают до появления шестерки, найти вероятность того, что кубик придётся.

Источник

Куб с окрашенными гранями распилен на n кубиков одинакового размера, которые перемешаны. Извлекаются 3 кубика. Найти вероятность того, что у них в сумме будет k окрашенных граней. 2.9 n = 729, k = 6.

Готовое решение: Заказ №8391

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Теория вероятности

Дата выполнения: 16.09.2020

Цена: 208 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Куб с окрашенными гранями распилен на n кубиков одинакового размера, которые перемешаны. Извлекаются 3 кубика. Найти вероятность того, что у них в сумме будет k окрашенных граней.

2.9 n = 729, k = 6.

Пусть событие A – у трёх извлечённых кубиков в сумме 6 окрашенных граней.

Событие A можно представить в виде суммы трёх несовместных событий:

где A ₁ – у двух кубиков по 3 окрашенные грани, у третьего – ни одной;

A ₂ – у одного кубика – 3 окрашенные грани, у другого – 2 грани, у третьего – 1 грань;

A ₃ – у всех трёх кубиков – по 2 окрашенные грани.

По теореме о вероятности суммы несовместных событий запишем:

Найдём вероятности событий A ₁ , A ₂ , A ₃ .

Очевидно, что при распиливании куба на n = 729 кубиков каждое ребро должно быть распилено на 3 √ n = 3 √729 = 9 частей. В результате получим:

8 кубиков с 3-мя окрашенными гранями;

12 ( 3 √ n – 2) = 12 · (9 – 2) = 84 кубика с 2-мя окрашенными гранями;

6 ( 3 √ n – 2) 2 = 6 · (9 – 2) 2 = 294 кубика с 1-й окрашенной гранью;

( 3 √ n – 2) 3 = (9 – 2) 3 = 343 кубика без окрашенных граней.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник

Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера. Определить вероятность того, что извлечённый кубик будет иметь

Готовое решение: Заказ №8390

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Теория вероятности

Дата выполнения: 29.08.2020

Цена: 208 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

2.20. Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера. Определить вероятность того, что извлечённый кубик будет иметь:

a. три окрашенные грани;

b. ровно две окрашенные грани;

c. ровно одну окрашенную грань.

Всего получено 1000 кубиков, каждый из которых с равной вероятностью может быть выбран. Следовательно, общее число равновероятных исходов:

При распиле каждая грань делится на равных отрезка. Окрашенными будут кубики внешнего слоя.

a. Пусть событие A состоит в том, что извлечённый кубик имеет три окрашенные грани.

Число кубиков с тремя окрашенными гранями равно числу вершин большого куба, то есть 8-ми. Следовательно, число исходов, благоприятствующих событию A, равно:

Вероятность события A, по классическому определению вероятности:

b. Пусть событие B состоит в том, что извлечённый кубик имеет ровно две окрашенные грани.

Две окрашенные грани будут у кубиков, которые содержат грань большого куба, но не содержат его вершину. Поскольку на каждой грани большого куба будет таких кубиков, а граней 12, то число кубиков с двумя

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник

Задачи на вероятность

Пример 2.11.

Куб с окрашенными гранями распилен на 27 одинаковых кубиков. Найдем вероятность того, что у выбранного наудачу кубика будет окрашена одна грань (две грани, три грани).

Общее число элементарных исходов в данном опыте N = = 27. Обозначим: А — событие, заключающееся в том, что у выбранного кубика окрашена одна грань; В — две грани и С — три грани. Событию А благоприятствует элементарных исходов (число граней у исходного куба), событию исходов (число ребер у исходного куба), а событию С — 8 исходов (число вершин у исходного куба). Поэтому

По этой ссылке вы найдёте полный курс лекций по теории вероятности:

Пример 2.12.

Из 33 карточек с написанными на них различными буквами русского алфавита наугад извлекаются пять карточек и располагаются слева направо в порядке извлечения. Найдем вероятность появления слова „РАДИО» (событие А).

Поскольку карточки обратно не возвращаются и порядок выбора существен, то общее число элементарных исходов равно числу размещений без повторений из 33 элементов по пять элементов:

Событию А благоприятствует только один элементарный исход (). Значит,

Возможно вам будут полезны данные страницы:

Пример 2.13.

Из колоды в 52 игральные карты выбирают наудачу три карты. Найдем вероятность того, что среди этих карт будут тройка „пик», семерка „пик», туз „пик».

Поскольку порядок выбора в данном случае не существен и карты обратно в колоду не возвращаются, то число элементарных исходов равно числу сочетаний без повторений из 52 элементов по три элемента, т.е.

Рассматриваемому событию А благоприятствует единственный исход (). Поэтому

Пример 2.14.

Группа, состоящая из восьми человек, занимает место за круглым столом. Найдем вероятность того, что два определенных человека окажутся сидящими рядом.

Так как упорядочивается все множество из восьми элементов, то мы имеем дело с перестановкой из восьми элементов. Поэтому

Рассматриваемому событию А благоприятствуют такие перестановки, когда два отмеченных лица садятся рядом: всего восемь различных пар мест за столом и за каждую пару мест данные лица могут сесть двумя способами. При этом остальные шесть человек могут разместиться на оставшихся местах произвольно. Значит,

Для сравнения приведем еще одно решение поставленной задачи. Заметим, что поскольку нас интересуют только два определенных лица, то порядок размещения остальных не играет роли. В свою очередь, если первый человек сел на определенное место, то второй может сесть на оставшиеся семь мест. При этом в двух случаях оба лица окажутся рядом и

Пример 2.15.

Из десяти первых букв русского алфавита составлены всевозможные трехбуквенные „слова». Найдем вероятность того, что случайно выбранное „слово» окажется „словом» „ИИИ».

Число различных „слов» равно числу размещений с повторениями из 10 элементов по три элемента, т.е.

Поскольку благоприятствующий исход только один, то

Пример 2.16. Опыт состоит в четырехкратном случайном выборе С возвращением одной буквы из букв алфавита „А», „Б», „К», „О» и „М“ и записывании результата выбора слева направо в порядке поступления букв. Найдем вероятность того, что в результате будет записано слово „МАМА».

Число элементарных исходов равно числу размещений с повторениями из пяти элементов по четыре элемента, т.е.

Слову „МАМА» соответствует лишь один исход. Поэтому

Пример 2.17.

В урне имеются четыре шара различного цвета. Наудачу из урны извлекают шар и после определения его цвета возвращают обратно. Найдем вероятность того, что среди восьми выбранных шаров будут только шары одного цвета (событие А)? будет по два шара разного цвета (событие В).

• Число элементарных исходов равно числу размещений

с повторениями из четырех элементов по восемь элементов.

Для того чтобы найти число исходов, благоприятствующих событию А, предположим сначала, что вынимают только шары первого цвета. Это можно сделать только одним способом. Аналогично только одним способом можно выбрать шары второго, третьего и четвертого цветов. Поэтому и

Число исходов, благоприятствующих событию В, равно числу тех сочетаний с повторениями из четырех элементов по восемь элементов, в которых каждый элемент повторяется по два раза, т.е.

Пример 2.18.

Первенство по баскетболу оспаривают 18 команд, которые путем жеребьевки распределены на две подгруппы по девять команд в каждой. Пять команд обычно занимают первые места. Найдем вероятность попадания всех лидирующих команд в одну подгруппу (событие А); трех лидирующих команд в одну подгруппу, а двух — в другую (событие В).

Пространство элементарных исходов в данном случае состоит из всевозможных способов выбрать из 18 команд, среди которых пять лидирующих, девять команд в первую подгруппу (тогда вторую подгруппу будут составлять оставшиеся девять команд), причем события А и В происходят тогда, когда в первую подгруппу попадет определенное число лидирующих команд и команд аутсайдеров.

Значит, мы имеем дело с гипергеометрической схемой, в которой к = 2, п = 18, тц = 5, т = 9.

Событие А происходит тогда, когда в первую подгруппу попадают или пять лидирующих команд и четыре команды-аутсайдера , или девять команд-аутсайдеров . Значит,

Аналогично событие В происходит тогда, когда в первую подгруппу попадут или три лидирующие команды и шесть команд-аутсайдеров или две лидирующие команды и семь команд-аутсайдеров . Таким образом,

Пример 2.19.

На бесконечную шахматную доску со стороной квадрата а наудачу бросают монету радиуса г, г

Пусть — координаты центра упавшей монеты. В силу бесконечности шахматной доски можно считать, что элементарные исходы данного эксперимента полностью определяются положением центра упавшей монеты относительно вершин квадрата, содержащаго этот центр.

Помещая начало координат в одну из вершин указанного квадрата (рис. 2.2), можно записать множество элементарных исходов в виде

Область А, соответствующая рассматриваемому событию, имеет вид

т.е. является квадратом со стороной . В соответствии с формулой геометрической вероятности находим

Пример 2.20.

В любые моменты интервала времени

равновозможны поступления в приемник двух независимых сигналов. Сигналы искажаются, если разность между моментами их поступления меньше т. Определим вероятность того, что сигналы будут искажены.

Изобразим случайные моменты поступления сигналов в приемник в виде точки на плоскости с координатами . Областью возможных значений является квадрат площадью (рис. 2.3). Сигналы будут искажены, если Эта область лежит между прямыми Площадь ее равна

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник