В полушар радиусом вписан куб таким образом

В полушар радиусом (корень из 3 / 2) вписан куб таким образом, что четыре его вершины лежат в большом круге шара, а остальные четыре вершины лежат на поверхности шара?

В полушар радиусом (корень из 3 / 2) вписан куб таким образом, что четыре его вершины лежат в большом круге шара, а остальные четыре вершины лежат на поверхности шара.

Решение во вложенном файле.

Куб вписан в шар радиуса корень из 3?

Куб вписан в шар радиуса корень из 3.

Шар радиуса 4см вписан в куб вычислить объем шара и объем куба?

Шар радиуса 4см вписан в куб вычислить объем шара и объем куба.

Куб вписан в шар радиуса корень из 3?

Куб вписан в шар радиуса корень из 3.

Найдите площадь поверхности куба.

Куб с ребром, равным корень из 2 см, вписан в шар?

Куб с ребром, равным корень из 2 см, вписан в шар.

В куб вписан шар?

Найдите объем шара, если объем куба равен 30.

Куб вписан в шар радиуса корень из 3 ?

Куб вписан в шар радиуса корень из 3 .

Найдите площадь поверхности куба.

В куб вписан шар радиус 3?

В куб вписан шар радиус 3.

Куб вписан в шар радиусом 3?

Куб вписан в шар радиусом 3.

Куб вписан в шар (вершины куба лежат на поверхности шара)?

Куб вписан в шар (вершины куба лежат на поверхности шара).

Поверхность куба равна 18.

Куб вписан в шар?

Найдите радиус шара, если ребро куба равно 10 корень из 3.

На этой странице вы найдете ответ на вопрос В полушар радиусом (корень из 3 / 2) вписан куб таким образом, что четыре его вершины лежат в большом круге шара, а остальные четыре вершины лежат на поверхности шара?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

180 — 53 = 127 ответ : 53 ; 127 ; 53 ; 127.

Источник

В полушар радиусом вписан куб таким образом

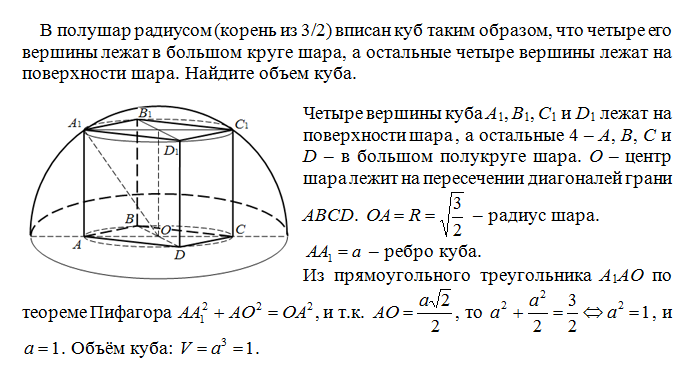
В полушар радиусом (корень из 3/2) вписан куб таким образом, что четыре его вершины лежат в большом круге шара, а остальные четыре вершины лежат на поверхности шара. Найдите объем куба.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Решение во вложенном файле.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

Нахождение радиуса вписанного в куб шара

В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.

Примечание: Напомним, что в любой куб можно вписать шар.

Для начала выполним чертеж.

• шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
• центр шара – точка O, которая также является центром куба.

Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:

R = a/2, где “a” – ребро куба (является стороной его грани).

Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.

Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.

Радиус вписанного шара через диагональ куба

Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:

Источник

Банк задач по теме «Комбинации круглых тел»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Лицей №159 Советского района г. Казани

Авторская работа на тему:

Подготовила: Салихова Флюра Тимергалиевна,

учитель математики

первой квалификационной категории

Казань 2011

2.1. Вписанные и описанные цилиндры ……………………………….………9

2.2. Вписанные и описанные конусы ………………………………….……. 13

2.3. Многогранники и сфера………………………………………….…………21

3. Задачи для решения …….…………………..………….……………….……………..…….26 3.1. Задачи с готовыми чертежами……………………………………..…………. …. 26 3 .2. Задачи на комбинации круглых тел……………………………………… …….…34

3.2.1. Цилиндр + прямоугольный параллелепипед…………..………………34

3.2.2. Цилиндр + призма …………………………………………………….…34

3.2.4. Цилиндр + шар …………………………………………………….……35

3.2.6. Конус + сфера и шар……………………………………………. …….. 36

3.2.7. Усеченный конус + сфера………………………………………. ……..37

3.2.8. Сфера + прямоугольный параллелепипед ………………. …………. 37

3.2.9. Задачи для поступающих в ВУЗы с решениями ………. ……….…..38

Заключение………………………………………………………………………… ………..….53 Использованная литература……………………………………………………. 54

Для успешного решения задач модернизации образования необходимы новые подходы к конструированию содержания школьных предметов, совершенствование технологий и методик обучения.

Одним из вариантов комплексного решения задач современного школьного образования являются учебные проекты, позволяющие формировать у учащихся способность к осуществлению практической деятельности – способность определять цель деятельности и планировать пути ее достижения, анализировать и оценивать результаты. Практическая значимость работы заключается в разработке серии стереометрических задач, посвященных организации деятельности учащихся по подготовке к сдаче ЕГЭ по геометрической линии. Проблема – низкий уровень соответствия умений и навыков, неумение использовать теоретические знания в практической деятельности.

Методы исследования: анализ методической и учебной литературы, базы данных математических задач «Задания для подготовки к единому государственному экзамену» для учащихся 10-х и 11-х классов. Предполагаемый продукт — банк тематических заданий для курса по выбору для учащихся 10-11-х классов по теме «Решение стереометрических задач по теме «Комбинации круглых тел»».

В контрольно измерительные материалы (КИМы) по математике включено две задачи по стереометрии. Одна во второй части, где требуется только записать правильный ответ, а вторая – в части С, среди заданий с развернутыми решениями. То есть, экзаменуемый должен построить чертеж, решить задачу и написать в бланке ответов ее развернутое решение. Моя цель – охарактеризовать основные типы задач по стереометрии, предлагаемых на ЕГЭ, сориентировать учащихся на тот теоретический материал, который может потребоваться и познакомить с тем, как правильно оформить решения. Задачи, предлагаемые во второй части, относятся главным образом к пирамидам, призмам, конусам, цилиндрам и предполагают вычисление углов между прямой и плоскостью, между плоскостями, а также вычисление площадей и объемов. Эти задачи относятся к среднему уровню сложности. Как правило, их решение сводится к применению одного – двух стереометрических фактов и вычислениям по известным формулам. Надо научить учащихся тому, чтобы они не хватались за первый пришедший в голову способ решения, а, некоторое время поразмыслив, постарались найти наиболее простой и нетрудоемкий способ – он существует.

Существуют проблемы и при изучении стереометрии. Формальные знания по этому разделу школьной математики обнаруживаются у большинства учащихся. Выявляется не только недостаточно сформированное пространственное представление учащихся, но и отсутствие умения выполнять проекционный чертёж и оперировать данными на нем. Выходом из сложившейся ситуации может выступить введение в процесс обучения дополнительного курса в рамках дисциплин по выбору. В связи с этим мной подобран материал для курса по выбору «Комбинации круглых тел», в рамках дисциплин по выбору, предназначенный для учащихся 10-11-х классов различных типов общеобразовательных учреждений. Цель данного курса по выбору, рассчитанного на 36 часа, заключается в ознакомлении, обучении и отработке определённых методов решения задач на комбинацию круглых тел и многогранников, ведущих к развитию пространственных представлений и воображения учащихся. Он также может быть рекомендован для параллельного изучения в курсе стереометрии темы «Многогранники» и «Круглые тела». Курс может читаться как для небольшого числа слушателей, так и для целого класса в рамках обязательного. При изучении данного курса по выбору рекомендую использовать компьютерные программы для построения пространственных чертежей. Они помогут, во-первых, осмыслить структуру проекционного чертежа, во-вторых, получить возможность правильно оперировать данными на нём. В процессе обучения решению стереометрических задач на комбинации необходимо выполнить ряд условий:

1) учитель и ученик в полной мере должны обладать необходимыми навыками работы на персональном компьютере;

2) предполагается, что стереометрия изучается в классах с профильным или

углубленным изучением математики;

3) класс оснащен ТСО, включающим в себя компьютеры и мультимедийный

4) разработана поурочная система индивидуализированного обучения учащихся.

Методический компонент включает в себя этапы организации деятельности учащихся. Введение каждого метода решения задач на построение осуществляется поэтапно. На информационном этапе осуществляется объяснение учителем сущности каждого метода решения с построениями. Он является одним из основных, учитель не только акцентирует внимание учеников на сущности каждого метода решения и построения, но и проводит пропедевтическую работу по обучению поэтапного построения на проекционном чертеже.

Второй практический этап предусматривает решение конкретной задачи. Решение задачи происходит при демонстрации метода решения задачи при помощи проектора или другого демонстрационного оборудования, акцентировании внимания на каждом этапе решения.

Третий этап (этап индивидуализации) требует индивидуального подхода к каждому учащемуся. Более сильные учащиеся после самостоятельного повторения и просмотра решения разобранной задачи приступают к решению новых задач предложенным методом с последующей коррекцией и проверкой решения учителем. Более слабые ученики после повторения приступают к решению ещё нескольких новых задач совместно с учителем, с акцентированием внимания на каждом шаге поэтапного решения, а уж затем переходят к самостоятельному решению, конечно же, при постоянном контроле учителя. Заключительным шагом в процессе обучения является домашнее задание по решению стереометрических задач данным методом. Оно может состоять из двух частей: обязательного минимума с многоуровневыми заданиями и дополнительной части. Банк заданий предоставляет учителю возможность свободного выбора методических путей и организационных форм обучения методом решения задач, проявления творческой инициативы.

Однако учителю, при этом следует иметь в виду следующие методические рекомендации.

учебно-воспитательный процесс должен строиться с учётом возрастных

возможностей и потребностей учащихся;

основной причиной не заинтересованности в прохождении курса по выбору является перегрузка; поэтому не следует стремиться к чрезмерному насыщению программы вопросами, дополняющими предложенную программу;

изучение предполагает, прежде всего, наполнение курса разнообразными,

интересными и сложными задачами, овладение основным программным материалом на более высоком уровне, а так же внедрением в процесс обучения соответствующего компьютерного программного обеспечения.

для поддержания интереса к предмету следует включать в процесс обучения занимательные задачи, сведения из истории математики, значительное место должно быть уделено решению задач, отвечающих требованиям поступления в вузы, где математика является профилирующим предметом;

в связи с тем, что курс по выбору могут посещать школьники с разным

уровнем подготовки, в процесс обучения на каждом этапе должны быть включены повторение и систематизация опорных знаний;

учебный процесс должен быть ориентирован на усвоение учащимися прежде всего, основного материала; при проведении текущего и итогового контроля знаний качество усвоение этого материала проверяется в обязательном порядке.

значительное место в учебном процессе должно быть отведено самостоятельной математической деятельности учащихся решению задач, проработке теоретического материала, подготовке докладов, рефератов и т.д.

очень важно организовать дифференцированный подход к учащимся, позволяющий избежать перегрузки и способствующий реализации возможностей каждого из них.

Тема “Разные задачи на многогранники, цилиндр, конус и шар” является одной из самых сложных в курсе геометрии 11 класса. Перед тем, как решать геометрические задачи, обычно изучают соответствующие разделы теории, на которые ссылаются при решении задач. В учебнике С.Атанасяна и др. по данной теме (стр. 138) можно найти только определения многогранника, описанного около сферы, многогранника, вписанного в сферу, сферы, вписанной в многогранник, и сферы, описанной около многогранника. В методических рекомендациях к этому учебнику (см. книгу “Изучение геометрии в 10–11-х классах” С.М.Саакяна и В.Ф.Бутузова, стр.159) сказано, какие комбинации тел рассматриваются при решении задач № 629–646, и обращается внимание на то, что “при решении той или иной задачи, прежде всего нужно добиться того, чтобы учащиеся хорошо представляли взаимное расположение указанных в условии тел”. Далее приводится решение задач №638(а) и №640.

Учитывая все выше сказанное, и то, что наиболее трудными для учащихся являются задачи на комбинацию шара с другими телами, необходимо систематизировать соответствующие теоретические положения и сообщить их учащимся.

Из учебника Л.С.Атанасяна на комбинацию шара

с призмой можно предложить задачи № 632, 633, 634, 637(а), 639(а,б).

с пирамидой можно предложить задачи № 635, 637(б), 638, 639(в),640, 641.

с усеченной пирамидой в учебнике Л.С.Атанасяна есть всего лишь одна задача (№ 636).

с круглыми телами можно предложить задачи № 642, 643, 644, 645, 646.

Поэтому прежде чем рассмотреть задачи из учебника я в своей работе предлагаю две ключевую задачу.

Ключевая задача: вывод обобщённой формулы для определения величины радиуса шара, описанного около многогранников и круглых тел.

Задача №1. Около шара описан цилиндр, площадь поверхности которого равен 9. Найдите площадь поверхности шара.

Площадь поверхности цилиндра вычисляется по формуле S = 2π R ( R + h ). Так как в цилиндр вписан шар, то h =2 R , отсюда, 9=6π R 2 , π R 2 = 1,5

Найдем площадь поверхности шара. R _ш = R _ц, поэтому S _ш =4π R 2 , S _ш = 4·1,5=6. Ответ: 6.

Задача №2. Найти радиус шара, описанного около правильного тетраэдра с ребром 6.

Предварительно построим на изображении правильного тетраэдра S АВС изображение центра описанного шара — точку О_1. . Для этого проведем апофемы SD и AD , SD = AD , так как дан правильный тетраэдр. Рассмотрим равнобедренный треугольник ASD . Каждая точка медианы DN равноудалена от концов отрезка AS . Поэтому точка О₁ — точка пересечения высоты SO и отрезка DN . Используя ключевую задачу

SO 2 = SA 2 — АО 2 , АО = 6 √3/3 = 2√3 ,

SO 2 = 6 2 — (2√3) 2 = 24 , SO = 2√6. Тогда S О₁ = 36/(2·2√6)= 3√6/2.

Вписанные и описанные цилиндры (с теоретическим материалом)

Сферу можно вписывать не только в многогранник, но

Определение. Сфера называется вписанной в цилиндр, если

она касается его оснований и боковой поверхности (касается

каждой образующей) (рис. 1). При этом цилиндр называется описанным около сферы.

Определение. Цилиндр называется вписанным в сферу, если

окружности оснований цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра (рис. 2).

Теорема. Если образующая цилиндра равна диаметру

его основания, то в него молено вписать сферу.

Доказательство. Заметим, что осевое сечение цилиндра в этом

случае является квадратом (рис. 3).

Впишем в него окружность. Будем теперь вращать квадрат вместе с вписанной в него окружностью вокруг оси цилиндра. В результате получим исходный цилиндр вместе с вписанной в него сферой.

Определение. Прямая призма называется вписанной в цилиндр,

если ее основания лежат на основаниях цилиндра, а боковыми

ребрами являются образующие цилиндра (рис. 4). При этом

цилиндр называется описанным около призмы.

Ясно, что около прямой призмы можно описать цилиндр тогда и только тогда, когда около ее основания можно описать окружность.

Определение. Касательной плоскостью к цилиндру

называется плоскость, проходящая через образующую цилиндра

и не имеющая с цилиндром других общих точек (рис. 5).

Определение. Прямая призма называется описанной около цилиндра,

если ее основания содержат основания цилиндра, а плоскости

боковых граней касаются цилиндра (рис. 6). При этом

цилиндр называется вписанным в призму.

Ясно, что в прямую призму можно вписать цилиндр тогда и только тогда, когда в ее основание можно вписать окружность.

Около прямой четырехугольной призмы описан

цилиндр, причем его высота больше радиуса основания,

а плоскость основания совпадает с плоскостью

основания цилиндра. Основание призмы – прямоугольник,

в котором диагональ и сторона образуют угол, тангенс которого равен . Боковая поверхность цилиндра равна , а расстояние между диагональю боковой грани призмы и скрещивающейся с ней диагональю основания равно . Найдите объем пирамиды.

1) Положим, а = AD , b = DC =

To гда радиус основания цилиндра будет равен Площадь боковой поверхности цилиндра по условию равна , откуда получаем первое уравнение, связывающее длину основания и высоту призмы:

2) Развернем призму так, чтобы боковая диагональ была перпендикулярна чертежу, то есть в виде точки F ( DC ₁): тогда диагональ АС будет видна в виде линии А’С’ плоскости, одновременно параллельной прямой DC ₁ и перпендикулярной плоскости чертежа. Значит, расстояние между прямой DC ₁ и параллельной ей плоскости, в которой лежит диагональ АС, будет равно перпендикуляру FE , опущенному на А’С’: то есть достаточно найти высоту треугольника AFC .

4)

По условию задачи длина F E равная , получаем второе уравнение, которое связывает неизвестные a , h : 28а 4 h 2 = 9(2а 4 + 3 a 2 h 2 ), объединяя которое с уравнением из 1), получаем:

Или a = 1 и h = 3

5) Объем призмы равен .

Одно из сечений пирамиды МАВС плоскостью, параллельной основанию, — равнобедренный треугольник со сторонами 0,1 и 0,2. Боковые грани образуют равные углы с плоскостью основания. Другая плоскость α, также параллельная основанию, пересекает высоту МО пирамиды в точке Р так, что MP : МО = 2 : 5. В образовавшуюся при этом усеченную пирамиду вписан прямой цилиндр с верхним основанием, вписанным в сечение пирамиды плоскостью α. Объем цилиндра равен 10,08π. Площадь сечения пирамиды, которое делит ее на две равные пирамиды, равна . Найдите площадь боковой поверхности пирамиды.

1) Из условия задачи ясно, что основание пирамиды – равно­бедренный треугольник, у которого боковая сторона в два раза больше основания. Другой вариант невозможен в силу невы­полнения неравенства треугольника. Положим, основание ВС = а,а АВ = ВС = 2а.

2) Рассмотрим плоскость α – сечение пирамиды, проходящее через точку Р. Это будет равнобедренный треугольник А₁В₁С₁, подобный треугольнику ABC основания с коэффициентом подобия . Тогда, используя подобие треугольников DOM и QPM , объем цилиндра можно представить как

где R = OD — радиус окружности, вписанной в основание пирамиды, а Н = ОМ – ее высота.

3) Выразим R – радиус окружности, вписанной в основание пирамиды, — через длину основания а треугольника ABC :

4) Ясно, что сечение пирамиды, которое делит ее на две равные пирамиды, можно провести только через высоту МО, перпендикулярно основанию ВС через его середину N. Это будет треугольник AMN с высотой H = МО. Выразим ее через длину основания а треугольника ABC :

5) Подставим найденные выражения 3), 4) для R и H в формулу 1) для цилиндра. Получим уравнение для неизвестной длины а основания пирамиды:

Откуда b = 20, R = , H = 7.

6) Чтобы найти площади боковых треугольников пирамиды, заметим, что их апофемы равны между собой:

Тогда площадь всей боковой поверхности пирамиды будет равна

Вписанные и описанные конусы

Рассмотрим вопрос о возможности вписать сферу в конус.

Определение. Сфера называется вписанной в конус, если

она касается его основания и боковой поверхности (касается

каждой образующей; рис. 1). При этом конус называется описанным около сферы.

Теорема. В конус можно вписать сферу.

Доказательство. Заметим, что осевым сечением

конуса является равнобедренный треугольник. Впишем в

него окружность (рис. 2). Будем теперь вращать треугольник вместе с вписанной в него окружностью вокруг оси конуса. В результате получим исходный конус вместе с вписанной в него сферой.

Определение. Конус называется вписанным в сферу, если вершина и окружность основания конуса лежат на сфере. При этом сфера называется описанной около конуса.

Теорема. Около конуса можно описать сферу.

Доказательство аналогично предыдущему.

Определение. Пирамида называется вписанной в конус, если ее основание лежит на основании конуса, а боковыми ребрами являются образующие конуса (рис. 3). При этом конус называется

Ясно, что около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность.

Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и не имеющая с конусом других общих точек.

Определение. Пирамида называется описанной около конуса, если ее основание содержит основание конуса, а плоскости боковых граней касаются конуса (рис. 4). При этом конус называется вписанным в пирамиду.

Ясно, что в пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность.

Сторона основания правильной четырехугольной пирамиды равна . Круг, вписанный в боковую грань, является основанием конуса, вершина которого совпадает с центром основания пирамиды. Найдите объем конуса.

1) Рассмотрим сечение пирамиды плоскостью SOE ,прове­денной через ее высоту SO и апофему SE грани DSC . В силу симметрии треугольник SOE будет плоскостью осевого сечения конуса. Высота OF треугольника SOE , опущенная на сторону SE , и будет высотой конуса. С другой стороны, точка F является центром окружности, вписанной в треугольник DSC .

2) Чтобы найти объем конуса по известной

длине отрезка ОЕ= 0,5а ,необходимо найти угол α = ے SEO ,

который позволяет вычислить высоту конуса h = OF – OE • sin α.

Для определения площади окружности с центром в точке F , необходимо найти другой угол β = ے SDE , тогда ее радиус будет равен r = EF = DE • tg ے EDF = , так как центр окружности F лежит на биссектрисе DF угла β = ے SDE .

3) Установим связь между углами α и β. Обозначим длину апофемы через b = SE , тогда из треугольника SOE , получаем

а из треугольника SDE имеем

С другой стороны, из треугольника SOE можно выразить радиус окружности через cos α :

4) Приравнивая выражения для радиуса окружности из 2) и 3), получаем уравнение для определения угла β

тогда приходим к уравнению

Так как угол β — острый, то Откуда радиус окружности из 2) равен . Чтобы найти высоту конуса h = OF , зная и FE = r , воспользуемся теоремой Пифагора для треугольника OEF :

5) Теперь окончательно вычисляем объем конуса:

Дана правильная треугольная пирамида со стороной основания, равной . Центр основания пира­миды является вершиной конуса, окружность основания которого вписана в боковую грань пирамиды. Найдите ра­диус основания конуса.

Основное внимание в решении должно быть приковано к равнобедренному треугольнику ABF , поскольку:

• радиус вписанной в него окружности ищется,

• его высота тесно связана с искомым радиусом через пря­моугольный треугольник ODF (точнее, через его извест­ный катет OD ).

1. О — центр Δ ABC (правильного):

AD = ( CD — медиана и высота)

=> OD = AD tg 30° ( ΔAOD ) =

2. E — центр вписанной окружности в Δ ABF (равнобедрен­ный):

=> Е принадлежит FD (— медиана и высота)

=> ED = r — радиус вписанной окружности.

3. OF перпендикулярен ABC (пирамида правильная),

ОЕ перпендикулярен BF (ось и основание конуса)

=> OD 2 = DE • FD (ОЕ — высота к гипотенузе Δ AOF )

=> FD =

4. , где (Δ E А D ) =

( ΔFAD ) =

=>

Дан конус с вершиной М, радиус основания которого равен 6. На окружности его основания выбраны точки А, В ,С так, что углы ВМА, АМС, СМВ равны 90° каждый. Точка F выбрана на дуге ВС окружности основания конуса, не со­держащей точки А, так, что объем пирамиды MABFC наи­больший. Найдите расстояние от точки F до плоскости МАВ.

Прежде всего, неплохо было бы определить

местоположе­ние точки F : коль скоро все остальные

вершины пирамиды фиксированы, то ее объем максимален, когда эта точка на ок­ружности наиболее удалена от хорды ВС.

Далее, исходная пирамида — конечно, правильная, и она полностью задана. Значит, остальное — дело техники (точнее, арифметики).

1. Объем V _MABFC — максимален, когда F — середина дуги ВС, т.к.:

а)

б) высота FP — максимальна, когда FP — серединный перпендикуляр к хорде ВС.

(т.к. МА = MB = МС и ے AM В = ے AMC = ے CMB = 90°)

3. К — середина АВ (=> Δ АО К — прямоугольный):

б) АВ = 2АК = 2•АО• cos 30° = 6 √3 ,

ОК, МК перпендикулярны АВ => ON перпендикулярен ABM .

5. FH — перпендикуляр к плоскости АВМ:

ΔAON ) = 2 : 1, т.к. FA — диаметр, ОА — радиус.

6. Δ ABM , ΔАМО , ΔОКМ — прямоугольные:

а)

б)

в)

г)

д) Начало формы

Задачи для самостоятельного решения

1. Дан конус с вершиной М, радиус основания которого равен 2 . На окружности его основания выбраны точки А,В,С так, что углы ВМА, АМС, СМВ равны 90° каждый. Точка F выбрана на дуге ВС окружности основания конуса, не содержащей точки А, так, что объем пирамиды MABFC наибольший. Найдите расстояние от точки F до плоскости МАВ.

2. Дан конус с вершиной М, радиус основания которого равен 6 . На окружности его основания выбраны точки А, В, С так, что углы ВМА, СМВ, АМС равны α каждый, причем . Точка F выбрана на дуге ВС окружности осно­вания конуса, не содержащей точки А, так, что объем пирамиды MABFC наибольший. Найдите расстояние от точ­ки F до плоскости МАВ.

3. Дан конус с вершиной М, радиус основания которого равен 2 . На окружности его основания выбраны точки А, В, С так, что углы ВМА, СМВ, АМС равны α каждый, причем . Точка F выбрана на дуге ВС окружности основания конуса, не содержащей точки А, так, что объем пирамиды MABFC наибольший. Найдите расстоя­ние от точки А до плоскости MBF .

4. Дан конус с вершиной М, радиус основания которого равен 4 . В основание этого конуса вписан четырехугольник ABCD так, что углы ВМА, СМВ, ВМС, AMD равны 60° каждый. На дуге ВС окружности основания конуса, не содержащей точки А, выбрана точка F так, что объем пи­рамиды MABFCD наибольший. Найдите расстояние от точки F до плоскости МАВ.

5. Дан конус с вершиной М, радиус основания которого равен 6 . В основание этого конуса вписан четырехугольник ABCD так, что углы ВМА, СМВ, ВМС, АМВ равны α каждый, причем . На дуге ВС окружности основания конуса, не содержащей точки А, выбрана точка F так, что объем пирамиды MABFCB наибольший. Найдите расстояние от точки F до плоскости МАВ.

6. Дан конус с вершиной М, радиус основания которого равен 2 . В основание этого конуса вписан шестиугольник ABCDEF так, что углы АМВ, ВМС, СМ D , D МЕ, EMF , FMA равны α каждый, причем . На дуге ВС окружности основания конуса, не содержащей точ­ки А, выбрана точка L так, что объем пирамиды MABLCDEF наибольший. Найдите расстояние от точки L до плоскости АВМ.

7. Дан конус с вершиной М, радиус основания которого равен и высота 4. Точки А, В, С лежат на окружности основания конуса так, что АВ — диаметр и ے AMC = 60°. На дуге ВС окружности основания конуса, не содержащей точки А, выбрана точка L так, что объем пирамиды MABLC наибольший. Найдите расстояние от точки L до плоскости AM С.

8. Дан конус с вершиной М, радиус основания которого равен 2 и высота 2 . Точки А, В, С лежат на окружности основания конуса так, что АВ — диаметр и ے AMC = 90°. На дуге ВС окружности основания конуса, не содержащей точки А, выбрана точка L так, что объем пирамиды MABLC наибольший. Найдите расстояние от точки L до плоскости AM С.

Многогранники вписанные в сферу

Определение. Многогранник называется вписанным в сферу, если все его вершины принадлежат этой сфере. Сама сфера при этом называется описанной около многогранника.

Теорема. Около любой треугольной пирамиды можно описать сферу, и притом только одну.

Доказательство. Обратимся к

доказательству аналогичной теоремы планиметрии.

С чего мы начинали? Прежде всего находили

геометрическое место точек, равноудаленных от

двух вершин треугольника, например А и В(рис. 1).

Таким геометрическим местом является серединный перпендикуляр, проведенный к отрезку АВ. Затем находили геометрическое место точек, равноудаленных от точек А и С.Это серединный перпендикуляр к отрезку АС. Точка пересечения этих серединных перпендикуляров и будет искомым центром О описанной около треугольника ABC окружности.

Рассмотрим теперь пространственную ситуацию и попробуем сделать аналогичные построения.

Пусть дана треугольная пирамида ABCD (рис. 2). Точки А, В, С определяют плоскость α. Геометрическим местом точек, равноудаленных от трех точек — А, В, С, является перпендикуляр, назовем его а, проведенный к плоскости α и проходящий через центр O ₁ описанной около треугольника ABC окружности. Геометрическим местом точек, равноудаленных от точек A , D , является плоскость, назовем ее β, перпендикулярная отрезку AD и проходящая через его середину — точку Е.

Плоскость β не перпендикулярна плоскости α и, следовательно, пересекает прямую а в некоторой точке О, которая и будет искомым центром описанной около треугольной пирамиды ABCD сферы. Действительно, в силу построения, точка О одинаково удалена от всех вершин пирамиды ABCD . Причем такая точка будет единственной, так как пересекающиеся прямая и плоскость имеют единственную общую точку.

Выясним, в каком случае около прямой призмы можно описать сферу.

Теорема. Около прямой призмы молено описать сферу тогда и только тогда, когда около основания этой призмы можно описать окружность.

Доказательство. Если около прямой призмы описана сфера, то все вершины основания призмы принадлежат сфере и, следовательно, окружности, являющейся

линией пересечения сферы и плоскости основания

(рис. 3). Обратно, пусть около основания

прямой призмы описана окружность с центром в точке О₁ и радиусом r . Тогда и около второго основания призмы можно описать окружность с центром в точке O ₂ и тем же радиусом r . Пусть О₁О₂ = d , О — середина отрезка О₁ O ₂. Тогда сфера с центром О и радиусом будет искомой описанной сферой.

Многогранники описанные около сферы

Окружность называется вписанной в многоугольник, если все стороны этого многоугольника касаются окружности. Сам многоугольник при этом называется описанным около окружности.

В планиметрии доказывалось, что в любой треугольник можно вписать окружность, и притом только одну. Для нахождения центра О впи­санной в треугольник ABC окружности, нужно провести биссектрисы углов А и B . Их точка пересечения О будет одинаково удалена от всех сторон треугольника и, следовательно, будет искомым центром вписанной окружности (рис. 1). Перейдем теперь к пространственным фигурам.

Определение. Многогранник называется описанным около сферы, если плоскости всех его граней касаются сферы. Сама сфера называется вписанной в многогранник.

Выясним сначала, какие сферы касаются одновременно двух пересекающихся плоскостей.

Пусть дан двугранный угол, образованный полуплоскостями α и β с общей граничной прямой с. Через прямую с проведем полуплоскость γ, делящую этот двугранный угол пополам (рис. 2). Такая полуплоскость называется биссектральной. Точки полуплоскости γ, не принадлежащие прямой с, обладают тем свойством, что расстояния от них до плоскостей α и β одинаковы. Если это расстояние принять за радиус сферы R , то сфера с центром на биссектральной полуплоскости и радиусом R будет касаться плоскости α и плоскости β. Сама биссектральная полуплоскость без прямой с дает геометрическое место центров сфер, лежащих внутри двугранного угла и касающихся плоскостей α и β.

Теорема. В любую треугольную пирамиду можно вписать сферу, и притом только одну.

Доказательство. Ясно, что центром вписанной сферы будет точка, одинаково удаленная от всех граней треугольной пирамиды. Для ее нахождения рассмотрим три биссектральные полуплоскости двугранных углов, образованных боковыми гранями пирамиды и основанием. Точка пересечения этих полуплоскостей будет одинаково удалена как от боковых граней, так и от основания, т. е. будет искомым центром вписанной сферы (рис. 3).

Выясним, в каком случае в прямую призму можно вписать сферу.

Теорема. В прямую призму можно вписать сферу

тогда и только тогда, когда в основание этой призмы можно

вписать окружность и высота призмы равна диаметру

Доказательство. Пусть в прямую призму вписана сфера с центром в точке О и радиусом R (рис. 4). Тогда высота призмы равна 2 R . Через центр О проведем сечение призмы плоскостью, параллельной основаниям. В сечении призмы будет многоугольник, равный многоугольнику основания, описанный около окружности, являющейся сечением сферы плоскостью. Таким образом, в основание призмы можно вписать окружность. Обратно, предположим, что в основание прямой призмы можно вписать окружность радиуса R , а высота призмы равна 2 R .Пусть О — середина отрезка, соединяющего центры окружностей, вписанных в основания. Тогда сфера с центром О и радиусом R будет искомой сферой, вписанной в призму.

В прямой круговой конус вписано два шара так, что шары касаются друг друга, каждый из них касается боковой поверхности конуса, центры шаров лежат на оси конуса, нижний (больший) шар касается основания конуса. Найдите объем конуса, если радиус верхнего шара равен а, нижнего — b .

Рассмотрим в сечении, проходящем через высоту SH конуса треугольник SHA . Пусть О и О₁ — центры большего и меньшего шаров, R — радиус основания конуса. Тогда ے A = ے O ₁ OC , . При этом

Найдем теперь объем конуса:

Ответ:

Задачи для самостоятельного решения

1. Отрезок PN , равный 8, — диаметр сферы. Точки М, L ле­жат на сфере так, что объем пирамиды PNML наиболь­ший. Найдите площадь треугольника KLT , где К и Т — се­редины ребер РМ и NM соответственно.

2. Отрезок АВ — диаметр сферы. Точки С, D лежат на сфере так, что объем пирамиды ABCD наибольший. Найдите ко­синус угла между прямыми СМ и АВ, если М — середина ребра BD .

3. Около правильной пирамиды FABC описана сфера, центр которой лежит в плоскости основания ABC пирамиды, площадь сферы равна 48π. Точка М лежит на ребре АВ так, что AM : MB = 3:5.

Точка Т лежит на прямой AF и равноудалена от точек Ми В. Найдите объем пирамиды ТАСМ.

4. Около правильной пирамиды FABC описана сфера, центр которой лежит в плоскости основания ABC пирамиды. Точка М лежит на ребре АВ так, что AM : MB = 2:7. Точка Т лежит на прямой AF и равноудалена от точек М и В. Объем пирамиды ТВСМ равен . Найдите радиус сферы, описанной около пирамиды FABC .

Задачи с готовыми чертежами

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.

В цилиндрический сосуд налили 200 см 3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см 3 .

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого?

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны 5/π . Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 2/ π. Найдите объем цилиндра, описанного около этой призмы.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.

Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.

Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.

Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3 , а высота равна 2.

Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.

Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.

Найдите объем цилиндра, площадь основания которого равен 1, а образующая равна 6 и наклонена к плоскости основания под углом 30 0 .

В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?

Найдите объем конуса, площадь основания которого равна 2, а образующая равна 6 и наклонена к плоскости основания под углом 30 0 .

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

Объем конуса равен 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите объем отсеченного конуса.

Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на π.

Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.

Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 6. Найдите его объем, деленный на π.

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на π.

Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на π.

Около куба с ребром √3 описан шар. Найдите объем этого шара, деленный на π.

Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.

Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на π.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.

Площадь большого круга шара равна 1. Найдите площадь поверхности шара.

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V / π .

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V / π .

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V / π .

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V / π .

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V / π .

Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V / π .

Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V / π .

Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V / π .

Цилиндр + прямоугольный параллелепипед

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 5,5. Найдите объем параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 9. Найдите объем параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 5. Объем параллелепипеда равен 50. Найдите высоту цилиндра.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 32. Найдите высоту цилиндра.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 64. Найдите высоту цилиндра.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 8. Найдите высоту цилиндра.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объем параллелепипеда равен 36. Найдите высоту цилиндра.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 9. Объем параллелепипеда равен 81. Найдите высоту цилиндра.

В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые ребра равны 2/π. Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые ребра равны 10/π. Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 9. Боковые ребра равны 1/π. Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 4. Боковые ребра равны 9/π. Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра равны 3/π. Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 4/π. Найдите объем цилиндра, описанного около этой призмы.

В цилиндр вписана прямая призма, в основании которой лежит прямоугольный треугольник. Как расположена ось цилиндра по отношению к граням прямой призмы? Можно ли утверждать, что две боковые грани прямой призмы взаимно перпендикулярны?

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 40.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 10.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 20.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 21.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 23.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 42.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 120.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 36.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 48.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 60.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 84.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 14.

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 11.

В конус вписан цилиндр с квадратным осевым сечением. Площадь боковой поверхности цилиндра равна площади основания конуса. Найдите угол a наклона образующей конуса к плоскости его основания.

Около шара описан цилиндр. Найдите отношение их объёмов и отношение площадей их поверхностей.

В сферу вписан цилиндр, площадь боковой поверхности которого составляет 2/5 площади сферы. Найдите отношение высоты цилиндра к диаметру его основания.

Объем конуса равен 48. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Объем конуса равен 96. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Объем конуса равен 40. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Объем конуса равен 152. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Объем конуса равен 112. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду.

В конус вписана пирамида, в основании которой лежит прямоугольный треугольник. Как расположена ось конуса по отношению к граням пирамиды?

В сферу вписан конус, радиус основания которого равен ½ радиуса сферы. Найдите угол при вершине осевого сечения конуса.

Около сферы радиуса r описан конус, высота которого равна h. Найдите площадь полной поверхности конуса.

В конус вписана сфера. Площадь сферы составляет 2/3 площади боковой поверхности конуса. Найдите образующую конуса, если радиус его основания равен R.

Около сферы радиуса 2 см описан конус, высота которого равна 6 см. Найдите площадь полной поверхности конуса

В шар радиуса R вписан конус. Объём конуса составляет ¼ объёма шара. Найдите высоту конуса.

Около шара радиуса 6 описан конус, объём которого в два раза больше объёма шара. Найдите высоту конуса.

В конус вписан шар. Докажите, что отношение площади полной поверхности конуса к площади поверхности шара равно отношению их объёмов.

В конус вписан шар, площадь поверхности которого равна площади основания конуса. Какую часть объёма конуса составляет объём шара?

В конус вписан шар и через их линию касания проведена плоскость. Найдите отношение объёма отсечённого конуса к объёму данного, если угол при вершине осевого сечения конуса равен 2α.

В конус, осевое сечение которого – равносторонний треугольник, вписан шар. Найдите объем конуса, если объем шара равен 8.

Около сферы описан усечённый конус, образующая которого составляет с большим основанием угол 45 0 . Площадь сферы равна 200 см 2 . Найдите площадь боковой поверхности усечённого конуса.

Площадь сферы составляет3/4 площади поверхности описанного около сферы усечённого конуса. Найдите радиусы оснований усечённого конуса и радиус сферы, если образующая усечённого конуса равна 12.

В сферу радиуса R вписан усечённый конус, образующая которого равна R √2, а угол наклона её к плоскости нижнего основания равен a. Найдите площадь полной поверхности усечённого конуса.

В сферу радиуса R вписан усечённый конус, образующая которого составляет с плоскостью основания угол b. Угол между диагоналями в осевом сечении конуса, обращённый к основанию, равен a. Найдите площадь осевого сечения конуса.

В сферу радиуса R вписан усечённый конус, высота которого равна h. Диагонали осевого сечения конуса перпендикулярны. Найдите объём усечённого конуса. Имеет ли задача решение, если а) h =2/3R, б) h =3/2R?

Сфера + прямоугольный параллелепипед

Прямоугольный параллелепипед описан около сферы радиуса 6. Найдите его объем.

Прямоугольный параллелепипед описан около сферы радиуса 8. Найдите его объем.

Прямоугольный параллелепипед описан около сферы радиуса 9.5 . Найдите его объем.

Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.

Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

Объем прямоугольного параллелепипеда, описанного около сферы, равен 125. Найдите радиус сферы.

Объем прямоугольного параллелепипеда, описанного около сферы, равен 343. Найдите радиус сферы.

Задачи для вступительных экзаменов в вузы с решениями

Задача 1 (МИЭТ, 2004). В правильную треугольную пирамиду с высотой и ребром основания вписан полушар так, что его бóльший круг лежит в плоскости основания пирамиды. Найдите радиус полушара.

Решение. 1 способ. Высота правильной пирамиды является геометрическим местом точек, равноудаленных от ее боковых граней. Поэтому центр O вписанного в правильную треугольную пирамиду SABC полушара совпадает с основанием ее высоты SO и находится в плоскости ASK , построенной на боковом ребре SA и апофеме SK пирамиды (рис. 1). Поскольку , , то по признаку перпендикулярности прямой и плоскости . Проведем в плоскости ASK отрезок ОМ так, чтобы . Так как , то . Следовательно, (по признаку перпендикулярности прямой и плоскости). Значит, ОМ – радиус полушара, вписанного в пирамиду SABC .

Точка О – центр основания АВС, поэтому

.

Рассмотрим прямоугольный треугольник SOK . По теореме Пифагора . Отсюда . Отметим, что OM – высота прямоугольного треугольника SOK , опущенная на гипотенузу SK . Площадь треугольника SOK может быть вычислена двумя способами: и . Следовательно,

.

Итак, радиус вписанного в пирамиду полушара равен . Ответ: .

2 способ. Достроим правильную пирамиду SABC до многогранника , отразив симметрично точку S относительно плоскости ABC и соединив полученную точку с вершинами основания A , B и C . Тогда, очевидно, в этот многогранник можно вписать шар. Причем его радиус равен радиусу полушара, вписанного, согласно условию задачи, в исходную пирамиду.

Воспользуемся известной формулой для радиуса шара, вписанного в многогранник ,

где V – объем, а – площадь полной поверхности многогранника. Тогда

,

.

Таким образом, .

Ответ: .

Задача 2 (МИЭТ, 2004). В правильную треугольную пирамиду с высотой и ребром основания вписан шар. Найдите радиус шара.

ешение. Пусть длина стороны основания , высота пирамиды (рис. 2). Найдем объем пирамиды: . Длина высоты основания . Тогда апофему l можно найти, воспользовавшись теоремой Пифагора .

Вычислим площадь полной поверхности пирамиды:

.

Воспользуемся формулой для радиуса шара, вписанного в многогранник: , где V – объем, а – площадь полной поверхности многогранника. Тогда .

Ответ: .

Задача 3 (МИЭТ, 2004). В конус с высотой 6 вписан куб с ребром 2 так, что основание куба лежит на основании конуса. Найдите объем конуса.

ешение. Пусть куб вписан в конус согласно условию задачи, точки и лежат на основании конуса, а точки и – на его боковой поверхности (рис. 3).

Плоскость грани куба параллельна основанию конуса и пересекает его боковую поверхность по окружности. Точки и являются вершинами квадрата, вписанного в окружность сечения. Высота SH конуса проходит через центр окружности сечения, а значит, пересекает . Проведем плоскость через пересекающиеся прямые и SH (осевое сечение конуса). Так как и перпендикулярны плоскости , то и . Поскольку точки и принадлежат осевому сечению , то и лежат в плоскости , .

Радиус основания конуса равен . Очевидно, что (диагональ квадрата со стороной 2), (т.к. – высота квадрата). Из подобия треугольников и следует, что . Следовательно, . Тогда объем конуса . Ответ: .

Задача 4 (МИЭТ, 1999). В конус вписан шар радиуса . Найдите объем конуса, если известно, что плоскость, касающаяся шара и перпендикулярная одной из образующих конуса, отстоит от вершины конуса на расстояние ( и угол при вершине в осевом сечении конуса тупой).

ешение. Обозначим плоскость, о которой идет речь в условии задачи, через . Треугольник (рис. 4) – сечение конуса плоскостью, перпендикулярной плоскости и проходящей через центр шара, – точка пересечения стороны B С с плоскостью , – радиус шара, перпендикулярный стороне B С, F – точка касания шара с плоскостью , – высота конуса. Заметим, что имеются две плоскости, касающиеся шара и перпендикулярные образующей . Однако, по условию, , поэтому возможен только случай, изображенный на рис. 4.

Тогда , . Так как углы , и – прямые, то – квадрат со стороной r . Следовательно, . Из теоремы Пифагора для треугольника получаем .

Далее, . Заметим, что треугольники и подобны (по двум углам). Следовательно, или .

И, наконец, объем конуса .

твет: .

Задача 5 (МИЭТ, 2002). Через сторону CD основания правильной четырехугольной пирамиды SABCD и центр вписанного в нее шара проведена плоскость. В каком отношении эта плоскость делит площадь боковой грани SAB , если боковое ребро пирамиды в 1,5 раза больше стороны основания?

Решение. Высота правильной пирамиды является геометрическим местом точек, равноудаленных от ее боковых граней. Поэтому центр вписанного в правильную треугольную пирамиду SABC шара лежит на ее высоте (рис. 5).

Ребро CD пирамиды параллельно ребру AB , лежащему в плоскости боковой грани SAB . Поэтому по признаку параллельности прямой и плоскости ребро CD параллельно грани SAB .

Так как секущая плоскость проходит через ребро CD и пересекает боковую грань SAB по отрезку PQ , то отрезок PQ параллелен ребру CD .

Из условий и по признаку параллельности прямых следует, что .

Так как , то треугольники SAB и SQP подобны по двум углам. Найдем коэффициент подобия треугольников SAB и SQP . Для этого рассмотрим сечение SKM пирамиды плоскостью, проходящей через апофемы SK и SM . Высота SO пирамиды лежит в плоскости SKM , поскольку .

Отрезок MN , проходящий через точку , лежит на биссекторе двугранного угла SCDA . – линейный угол двугранного угла SCDA . Поэтому отрезок MN является биссектрисой треугольника SKM . По свойству биссектрисы .

Пусть , тогда , , . Таким образом, . Отсюда , .

Коэффициент k подобия треугольников SAB и SQP равен отношению их высот SK и SN : . Тогда отношение площадей треугольников SAB и SQP равно квадрату коэффициента подобия, т. е. . Таким образом, , или . Итак, . Ответ: .

Задача 6 (МИЭТ, 2002). Через сторону основания правильной треугольной пирамиды и центр вписанного в нее шара проведена плоскость. В каком отношении эта плоскость делит объем пирамиды, если высота пирамиды в 13 раз больше радиуса вписанного в нее шара?

ешение. Высота правильной пирамиды является геометрическим местом точек, равноудаленных от ее боковых граней. Поэтому центр O вписанного в правильную треугольную пирамиду SABC шара лежит на ее высоте . Рассмотрим сечение SAP пирамиды плоскостью, проходящей через апофему SP и боковое ребро SA (рис. 6). Высота пирамиды лежит в плоскости SAP , поскольку .

Отрезок MP , проходящий через точку , лежит на биссекторе двугранного угла SC В A . – линейный угол двугранного угла SC В A . Поэтому отрезок MP является биссектрисой треугольника SAP . А значит, также биссектриса в треугольнике .

Рассмотрим вначале треугольник . Поскольку по условию , то . По свойству биссектрисы . Отсюда .

Точка – центр правильного треугольника , поэтому . Значит, .

Рассмотрим теперь треугольник . По свойству биссектрисы . Отсюда , а значит, . Опустим перпендикуляр из точки M на основание пирамиды. Прямоугольные треугольники и подобны, т.к. острый угол A у них общий. Поэтому .

Найдем теперь отношение объемов пирамид и с общим основанием . Очевидно, что отношение их объемов равно отношению высот. Следовательно, . Таким образом, .

Ответ: .

Задача 7 (МИЭТ, 1999). В правильной четырехугольной пирамиде сторона основания равна b , а двугранный угол при основании равен . Найдите площадь сечения пирамиды плоскостью, проведенной параллельно плоскости основания через центр вписанного в пирамиду шара.

ешение. Пусть – правильная четырехугольная пирамида, – ее высота, – высота боковой грани (рис. 7). Высота правильной пирамиды является геометрическим местом точек, равноудаленных от ее боковых граней. Поэтому центр O вписанного в правильную четырехугольную пирамиду SABCD шара лежит на ее высоте . Тогда двугранный угол при основании равен , а центр вписанного в пирамиду шара (точка О) является пересечением и биссектрисы угла . Из подобия пирамиды и пирамиды, отсекаемой от нее плоскостью, проведенной параллельно плоскости основания через центр вписанного шара, получаем . , , , . Тогда .

Таким образом, площадь сечения . Ответ: .

Задача 8 (МИЭТ, 1999). Около правильной четырехугольной пирамиды описан шар. Через центр шара параллельно плоскости основания пирамиды проведена плоскость. Площадь сечения пирамиды плоскостью равна S . Найдите сторону основания пирамиды, если угол между ее противоположными боковыми ребрами равен .

Решение. Высота правильной пирамиды является геометрическим местом точек, равноудаленных от ее вершин основания. Поэтому центр O описанного около правильной четырехугольной пирамиды SABCD шара лежит на ее высоте . Поскольку угол между противоположными боковыми ребрами пирамиды острый, то центр описанного шара расположен над плоскостью ее основания. Рассмотрим сечение пирамиды плоскостью, проходящей через ее противоположные боковые ребра и (рис. 8).

Тогда – диагональ квадрата, являющегося сечением пирамиды через центр O описанного около нее шара, а – диагональ основания пирамиды . Высота является также биссектрисой и медианой равнобедренного треугольника . Поэтому , . Отметим также, что . Поскольку, согласно условию, площадь сечения , то .

Рассмотрим прямоугольный треугольник . Найдем радиус R описанного около пирамиды шара: .

Треугольник равнобедренный, т.к. . Поэтому . Следовательно, .

Рассмотрим теперь прямоугольный треугольник :

.

Значит, сторона a основания пирамиды .

Ответ: .

адача 9 (МИЭТ, 2000). В шар радиуса R вписана правильная усеченная четырехугольная пирамида, у которой большее основание проходит через центр шара, а боковая грань наклонена к плоскости основания под углом . Найдите объем усеченной пирамиды.

Решение. Высота правильной усеченной пирамиды, проведенная через центры ее оснований, является геометрическим местом точек, равноудаленных от вершин каждого из оснований (если рассматривать основания по отдельности). Поэтому центр описанного около правильной усеченной четырехугольной пирамиды шара лежит на ее высоте совпадает, согласно условию, с точкой О (рис. 9а).

Пусть M и – середины и соответственно. Боковая грань является равнобедренной трапецией, поэтому . Так как, очевидно, , то – линейный угол двугранного угла, образованного боковой гранью усеченной пирамиды с плоскостью нижнего основания. По условию и . Тогда . Кроме того, . Далее, , откуда . Рассмотрим сечение шара и пирамиды плоскостью (рис. 9б). Имеем: . Положим . Тогда . Отсюда . Возведем в квадрат: , или . Отсюда , . Корень не подходит, а удовлетворяет условию задачи. Вычислим теперь остальные элементы усеченной пирамиды. Имеем: , , . Следовательно, объем усеченной пирамиды

.

Ответ: .

Задача 10 (МИЭТ, 2000). В полушар радиуса R вписан в правильную усеченную четырехугольную пирамиду так, что большее основание пирамиды лежит в плоскости большого круга полушара. Найдите объем усеченной пирамиды, если ее боковая грань наклонена к плоскости основания под углом .

Решение. Высота правильной усеченной пирамиды, проведенная через центры ее оснований, является геометрическим местом точек, равноудаленных от ее боковых граней. Поэтому центр вписанного в правильную усеченную четырехугольную пирамиду полушара лежит на ее высоте и совпадает, согласно условию, с точкой О (рис. 10а). Пусть a и b стороны основания правильной усеченной четырехугольной пирамиды . Тогда ее высота . Р

ассмотрим сечение пирамиды плоскостью, проходящей через параллельно (рис. 10б). Тогда , а значит, и . Следовательно, . Далее, поскольку плоскость проходит через , то точки K и P – середины и соответственно. Боковая грань является равнобедренной трапецией, поэтому . Таким образом, – линейный угол двугранного угла, образованного боковой гранью усеченной пирамиды с плоскостью нижнего основания. Аналогично также является линейным углом двугранного угла . По условию . Кроме того, , .

Проведем из точки O перпендикуляр к боковой стороне равнобедренной трапеции (рис. 10б). Тогда . Рассмотрим прямоугольный треугольник . Найдем гипотенузу : . Следовательно, сторона нижнего основания усеченной пирамиды , а площадь нижнего основания .

Опустим из вершины P трапеции (рис. 10б) перпендикуляр к стороне . Тогда . Рассмотрим прямоугольный треугольник . Найдем катет : . Отсюда . Следовательно, сторона верхнего основания усеченной пирамиды , а площадь верхнего основания .

Таким образом, объем усеченной пирамиды . Ответ: .

Задача 11 (МИЭТ, 2001). Периметры оснований правильной треугольной усеченной пирамиды относятся, как . Сфера с центром, расположенным в плоскости бóльшего основания, касается другого основания и всех остальных граней пирамиды. Найдите углы, образованные боковыми ребрами пирамиды с ее основаниями.

Решение. Высота правильной усеченной пирамиды, проведенная через центры ее оснований, является геометрическим местом точек, равноудаленных от ее боковых граней. Поэтому центр вписанного в правильную усеченную треугольную пирамиду шара лежит на ее высоте и совпадает, согласно условию, с точкой О (рис. 11а). Причем центр верхнего основания усеченной пирамиды является точкой ее касания с шаром. Пусть . Тогда . Отсюда , .

ассмотрим сечение пирамиды плоскостью, проходящей через высоты и ее оснований (рис. 11б). Отметим, что лежит в плоскости сечения. Проведем высоту трапеции . Очевидно, что . Из треугольника :

, ,

где – искомый угол наклона бокового ребра к основанию (так как перпендикулярен к основаниям и , то ; следовательно, – проекция наклонной ).

Чтобы учесть касание с боковыми гранями, рассмотрим трапецию . Имеем: , .

Треугольники и равны по катету () и острому углу . Значит, . По теореме Пифагора . Следовательно, . Отсюда

 .

Поскольку угол – острый, то . Таким образом, .

Ответ: .

Задача 12 (МИЭТ, 1998). Из всех правильных треугольных призм, вписанных в полусферу радиуса R так, что плоскость основания призм совпадает с плоскостью, ограничивающей полусферу, выбрана призма наибольшего объема. Найдите площадь полной поверхности этой призмы.

Решение. Пусть – правильная призма. Нижнее основание лежит в плоскости, ограничивающей полусферу. Верхнее основание вписано в окружность, полученную пересечением полусферы плоскостью, проходящей через точки , лежащие на полусфере (рис. 12). Пусть – центр полусферы, – центр окружности, в которую вписано верхнее основание призмы. Тогда отрезок – радиус этой окружности, – высота призмы, – радиус полусферы.

оложим . Из треугольника находим . Длина стороны правильного треугольника , выраженная через радиус описанной окружности, равна , а его площадь равна . Тогда объем призмы равен , или . В силу условия задачи . Найдем наибольшее значение функции на промежутке . Функция принимает наибольшее значение при наибольшем значении функции . Найдем критические точки функции :

.

при и . Точка не принадлежит интервалу . Производная функции при переходе через меняет знак с «плюса» на «минус», следовательно, – точка максимума. Так как на промежутке функция имеет единственную точку экстремума, причем это точка максимума, то ее наибольшее значение, а значит, и наибольшее значение объема призмы, будет при . Следовательно, сторона основания призмы с наибольшим объемом равна , а высота – . В этом случае

.

Ответ: .

Задачи для самостоятельного решения

Задача 1. В правильную треугольную пирамиду с ребром основания вписан полушар так, что его больший круг лежит в плоскости основания пирамиды. Найдите высоту пирамиды.

Задача 2. В правильную треугольную пирамиду с высотой вписан шар радиуса . Найдите длину ребра основания пирамиды.

Задача 3. В конус с радиусом основания 6 вписан куб с диагональю основания, равной 8, так, что основание куба лежит на основании конуса. Найдите объем конуса.

Задача 4. В конус вписан шар. Найдите объем конуса, если известно, что плоскости, касающиеся шара и перпендикулярные одной из образующих конуса, отстоят от вершины конуса на расстояния и ( и угол при вершине в осевом сечении конуса острый).

Задача 5. Через сторону AF основания правильной шестиугольной пирамиды SABCDEF и центр вписанного в нее шара проведена плоскость. В каком отношении эта плоскость делит площадь боковой грани SCD , если высота SO пирамиды делится точкой в отношении : 1, считая от вершины S ?

Задача 6. Через сторону основания правильной треугольной пирамиды и центр вписанного в нее шара проведена плоскость. В каком отношении эта плоскость делит объем пирамиды, если ее боковое ребро в 3,5 раза больше стороны основания?

Задача 7. В правильной треугольной пирамиде сторона основания равна a , а двугранный угол при основании равен . Найдите площадь сечения пирамиды плоскостью, проведенной параллельно плоскости основания через центр вписанного в пирамиду шара.

Задача 8. Дана правильная четырехугольная пирамида со стороной основания, равной a , и плоским углом при вершине, равным . Найдите площадь сечения пирамиды плоскостью, содержащей центр описанного около пирамиды шара и параллельной плоскости основания.

Задача 9. Шар радиуса R вписан в правильную усеченную четырехугольную пирамиду, боковое ребро которой составляет с плоскостью основания угол, равный . Найдите объем усеченной пирамиды.

Задача 10. В правильную усеченную четырехугольную пирамиду, боковая грань которой наклонена к плоскости основания под углом , вписан полушар так, что бóльшее основание пирамиды лежит в плоскости большого круга полушара. Найдите площадь боковой поверхности усеченной пирамиды, если сторона ее мéньшего основания равна a .

Задача 11. Боковые ребра правильной треугольной усеченной пирамиды образуют с плоскостью основания угол, равный . Мéньшее из оснований проходит через центр сферы, которая касается другого основания и продолжений всех остальных граней пирамиды. Найдите отношение периметров оснований.

Задача 12. Из всех цилиндров, вписанных в полусферу радиуса R так, что плоскость основания цилиндров совпадает с плоскостью, ограничивающей полусферу, выбран цилиндр, имеющий наибольший объем. Найдите площадь его боковой поверхности. Ответы. 1. . 2. . 3. . 4. . 5. . 6. . 7. . 8. . 9. . 10. . 11. . 12. .Конец формы

Предлагаемый курс, частично отраженный в настоящей работе, показывает, что применение дифференцированного обучения и информационных технологий на уроках и во внеурочной деятельности расширяет возможности творчества как учителя, так и учеников, повышает интерес к предмету, стимулирует освоение учениками довольно серьезных тем по математике, что, в итоге, ведет к интенсификации процесса обучения. Без дополнительной подготовки только на уроках геометрии среднему ученику невозможно достичь обоснованного решения стереометрических задач. Групповая подготовка по уровню подготовленности дает реальную помощь при подготовки к сдаче ЕГЭ. Для высокой эффективности урока, конечно, необходима тщательная подготовка, продуманность всех этапов урока, четкое распределение на все виды работ, нужна разработка ключевых ситуаций и опорные знания по планиметрии. Тем, кто стремиться к познанию нового, нет преград и в жизни, и в учении. Хвала тем, кто по силу возможностей стремиться к этому. Моя задача – привить интерес к решению таких задач, направить ученика, дать ему материал для размышления и по мере необходимости помочь ему.

Источник