В кубе abcda1b1c1d1 ребро равно a точка k принадлежит

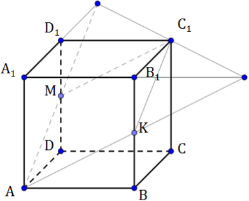
В кубе ABCDA1B1C1D1 ребро равно a , точка K принадлежит BB1. B1K : KB = 1:4
Точка L принадлежит DD1 , B1L : LD=3:1 .Постройте точку F пересечение прямых KL и BD, найдите длину отрезка BF.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

В плоскости диагонального сечения куба имеем 2 подобных треугольника BKF и DLF.
Пусть DF = х.
Из задания получаем ВД = а√2, КВ = 4а/5, DL = а/4.
Составим пропорцию: (ВД+х)/х = ВК/DL.
(а√2+х)/х = (4а/5)/(а/4).
(а√2+х)/х = 16/5.
5а√2+5х = 16х.
11х = 5√2а.
х = DF = (5√2а)/11.
ВF = ВD + DF = а√2 + (5√2а)/11 = (16√2а)/11.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

14. Стереометрия

Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.

Примеры ответов: 7 или здесьисейчас или 3514

Найдите площадь сечения, вершинами которого являются вершина А и середины рёбер ВВ₁ и DD₁единичного куба АВСDA₁B₁C₁D₁.

Дополнительное построение К – середина ребра ВВ₁ и М – середина ребра DD₁.

Строим сечение методом следов:

Соединяем вершины, лежащие в одной грани, А и К, А и М.
Продлеваем прямые АК и А₁В₁ до пересечения. Также прямые АМ и A₁D₁.
Соединяем точки и видим, что прямая, проходит через точку С₁, которая принадлежит нашему сечению.
Соединяем оставшиеся точки.

Сечением является ромб. Найдем его сторону по теореме Пифагора:

Большая диагональ куба является диагональю куба – АС₁.

Найдем угол АКС₁ по теореме косинусов:

$AC_1^2=AK^2+KC_1^2-2\cdot AK\cdot KC_1\cdot\cos AKC_1 \\[5pt] 3=\displaystyle\frac<5><4>+\frac<5><4>-2\cdot\frac<5><4>\cdot\cos AKC_1 \\[2pt] \cos AKC_1=-\displaystyle\frac<1><5>$

Найдем площадь искомого сечения:

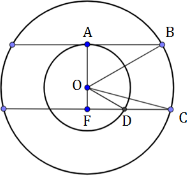
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5. Найдите площадь сечения большего шара плоскостью α.

Сечение шара плоскостью – круг.

Дополнительное построение – плоскость α имеет радиус АВ, плоскость β – FD и FC.

Площадь сечения большего шара плоскостью, параллельной первоначальной плоскости, равна 5. Значит: $S=\pi R^2=\pi\cdot AB^2=5$

Аналогичным образом найдем $FD^2=\displaystyle\frac<7><\pi>$

Для того, чтобы найти площадь искомого сечения, надо знать, чему равно CF 2 .

Применим теорему Пифагора:

Вычтем из одного уравнения другое.

Применим еще раз теорему Пифагора:

$OA^2+AB^2-OD^2=FC^2-FD^2 \\[3pt] OD=OA\rightarrow AB^2=FC^2-FD^2 \\ FC^2=AB^2+FD^2=\displaystyle\frac<5><\pi>+\frac<7><\pi>=\frac<12><\pi>$

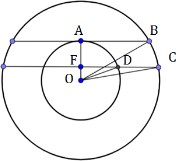
Также возможен случай, когда плоскости будут по одну сторону от центра. Решение будет аналогичным.

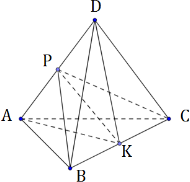
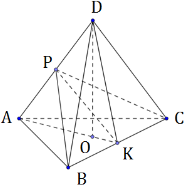
В треугольной пирамиде ABCD двугранные углы при рёбрах AD и BC равны. AB = BD = CD = AC = 5.

б) Найдите объем пирамиды, если двугранные углы при AD и BC равны 60.

1) Дополнительное построение:

2) Треугольники АВС и АBD равнобедренные по условию, значит, АК и BP будут являться медианами по свойству равнобедренного треугольника. Тогда DK, СР также являются одновременно медианой и высотой.

Тогда ∠BPC – линейный угол двугранного угла при ребре AD, ∠AKD — линейный угол двугранного угла при ребре ВС. Из условия имеем: ∠BPC = ∠AKD.

3) РК медиана, биссектриса и высота в треугольниках ВРС и AKD. Тогда PK ⊥ BC и PK ⊥ AD.

Тогда, треугольник BPK равен треугольнику АКР по углу

$\angle BPK=\displaystyle\frac<1><2>\angle BPC=\frac<1><2>\angle AKD=\angle AKP$ и катету РК.

Из равенства треугольников следует, что BK = AP.

$BK=\displaystyle\frac<1><2>BC \\[3pt] AP=\displaystyle\frac<1><2>AD$

1) По данным пункта б: ∠BPC = ∠AKD = 60°, тогда треугольники АКD и ВРС равносторонние. Пусть сторона каждого такого треугольника будет равна х.

2) Дополнительное построение. Пусть DO⊥ AK.

$\left\<\beginBC\perp KD\ (&по\ доказанному\ в\ пункте\ а) \\ BC\perp AK\ (&по\ доказанному\ в\ пункте\ а) \\ &KD\cap AK=K\end\right.\!\!\!\Rightarrow BC\perp AKD\ <(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)>$

Из доказанного следует, что BC ⊥ OD. Значит:

То есть, OD – высота пирамиды.

3) AK = x по построению, тогда $BK=\displaystyle\frac<2>.\ AB=5$.

Треугольник АВК прямоугольный, значит:

4) Высота пирамиды и равностороннего треугольника равна:

5) Площадь основания равна:

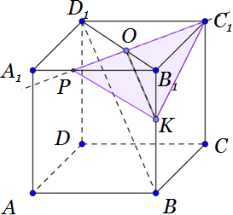
$S_=\displaystyle\frac<1><2>AK\cdot BC=\frac<1><2>\cdot x\cdot x=\frac<1><2>\cdot 2\sqrt<5>\cdot 2\sqrt<5>=10 \\ V=\displaystyle\frac<1><3>\cdot h\cdot S_=\frac<1><3>\cdot\sqrt<15>\cdot 10=\frac<10\sqrt<15>><3>$

В кубе $ABCDA_1B_1C_1D_1$ все рёбра равны 5. На его ребре BB₁ отмечена
точка K так, что KB = 3. Через точки K и С₁ проведена плоскость α, параллельная прямой BD₁.

а) Докажите, что $\displaystyle\frac=\frac<1><2>$, где P — точка пересечения плоскости α с ребром A₁B₁.

б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

а) 1. Дополнительное построение.

Пусть B₁D₁ пересекается с построенной прямой в точке О.

Прямая BD₁параллельная плоскости С₁ОК, так как параллельна как минимум одной прямой ОК (по построению), лежащей в этой плоскости.

2) Через точку С₁ и О проведем прямую. Пусть прямая С₁О пересекается с A₁B₁в точке Р. Точка Р – точка пересечения плоскости α с ребром A₁B₁.

3) В треугольнике BB₁D отрезок ОК параллелен BD₁. Значит отрезок ОК делит треугольник BB₁D на 2 подобных (признак подобия по 2 углам).

Что и требовалось доказать.

Ребро РВ₁ перпендикулярно В₁С₁К, так как $ABCDA_1B_1C_1D_1$ — куб, а значит является высотой пирамиды.

Найдем объем другой части куба.

Из объема всего куба вычтем объем пирамиды.

Источник

В кубе abcda1b1c1d1 ребро равно a точка k принадлежит

а) Докажите, что расстояние от вершины A₁ до прямой BK равно ребру куба.

б) Найдите угол между плоскостями KBA₁ и BCC₁.

а) Пусть AB = a, тогда и

В треугольнике A_{1 BK по теореме косинусов}

Опустим перпендикуляр A_{1 H из вершины A₁ на прямую BK Отрезок A_{1 H — высота треугольника A_{1 BK.}}}

Следовательно, расстояние от вершины A₁ до прямой BK равно ребру куба.

б) Найдём площадь треугольника A₁BK.

Проекцией этого треугольника на плоскость BCC₁ является треугольник BB₁C₁.

Площадь этого треугольника Отношение площадей треугольников BB₁C₁ и A_{1 BK. является косинусом угла между плоскостями и Следовательно,}

Тогда искомый угол

Ответ: б)

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Источник В кубе abcda1b1c1d1 ребро равно a точка k принадлежит Задание 14. В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре ВВ1 отмечена точка K так, что KB=3. Через точки K и C1 проведена плоскость α, параллельная прямой BD1. а) Докажите, что A1P:PB1 =2:1, где Р — точка пересечения плоскости α с ребром А1В1. б) Найдите угол наклона плоскости α к плоскости грани ВВ1С1C. а) Проведём через точку K прямую, параллельную BD1. Пусть эта прямая пересекает плоскость грани A1B1C1D1 в точке L. Прямая KL лежит в плоскости BB1D1, значит, точка L лежит на диагонали B1D1. Более того, B1L:LD1 =В1K:KB=1:3. Прямая C1L пересекает ребро А1В1 в точке Р, принадлежащей плоскости α. Треугольники B1LP и D1LC1 подобны, поэтому B1P:D1C1=B1L:D1L=1:3. Значит, A1Р:РВ1 =2:1. б) Опустим из точки перпендикуляр В1Н на C1K. По теореме о трёх перпендикулярах прямые РН и C1K перпендикулярны. Значит, угол B1HP искомый. Поскольку А1Р:РВ1 = 2:1, получаем PB1 = 4/3. В прямоугольном треугольнике B1C1K: . . Ответ: . Источник Оцените статью > Свежие записи Как найти датчик давления масла на Шкоде Октавия: руководство пользователя. Где находится датчик температуры воздуха на Шевроле Орландо? Как проверить датчик температуры испарителя в Chevrolet Aveo T300 Чувствительность датчика удара приказ дз: что это и как работает Рельсы с датчиком в майнкрафт: что это такое? Вам также может понравиться kak-pochistit-datchik-map-gbo-4-pokoleniya-wpvvobma ��JFIF«��C (1#%(:3=Mqypdx\egc��C//cB8Bcccccccccccccccccccccccccccccccccccccccccccccccccc��» 0178 Где находится датчик давления масла Volvo D13 FM? Volvo d13 датчик давления масла fm где находится Датчик 0194 Где находится датчик включения вентилятора Deu Espero: место установки и подробная инструкция Где находится датчик включения вентилятора дэу эсперо 0261 Местоположение датчика коленвала на Daewoo Nexia 16V: подробная инструкция Где находится датчик коленвала daewoo nexia 16 клапанов 0238 Где находится датчик скорости на Газель Бизнес Эвотек: подробная инструкция Где находится датчик скорости газель бизнес эвотек 0231 Где находится кислородный датчик на Opel Astra H Где находится кислородный датчик опель астра h Кислородный 0166 Где правильно установить датчик температуры двигателя для сигнализации Старлайн А93? Где устанавливают датчик температуры двигателя сигнализации 0140 Где находится датчик включения вентилятора на автомобиле Tagaz Accent? Датчик включения вентилятора акцент тагаз где находится 0168 © 2024 Юридический портал Adblock detector

Критерии оценивания выполнения задания

Баллы

Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)

Получен обоснованный ответ в пункте б)

имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Источник

В кубе abcda1b1c1d1 ребро равно a точка k принадлежит

Задание 14. В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре ВВ1 отмечена точка K так, что KB=3. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.

а) Докажите, что A1P:PB1 =2:1, где Р — точка пересечения плоскости α с ребром А1В1.

б) Найдите угол наклона плоскости α к плоскости грани ВВ1С1C.

а) Проведём через точку K прямую, параллельную BD1. Пусть эта прямая пересекает плоскость грани A1B1C1D1 в точке L. Прямая KL лежит в плоскости BB1D1, значит, точка L лежит на диагонали B1D1. Более того, B1L:LD1 =В1K:KB=1:3.

Прямая C1L пересекает ребро А1В1 в точке Р, принадлежащей плоскости α. Треугольники B1LP и D1LC1 подобны, поэтому B1P:D1C1=B1L:D1L=1:3. Значит, A1Р:РВ1 =2:1.