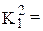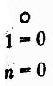«Сумма к-мерных граней n-мерного куба (к=0,1. n)»
«Сумма к-мерных граней n-мерного куба (к=0,1. n)»
Вначале введём некоторые понятия:
вместо слова «точка» мы будем говорить «0-мерный куб», вместо слова «отрезок» — «1-мерный куб», вместо слова «квадрат» — «двумерный куб» и т д., а рассматривать мы будем произвольный n-мерный куб.
Далее, вершину n-мерного куба будем называть 0-мерной гранью, ребро n-мерного куба — одномерной гранью и т. д. Сам n-мерный куб будет называться n-мерной гранью.
Таким образом, у отрезка, или, что то же самое, одномерного куба две нульмерные грани и одна одномерная грань, у обычного трехмерного куба 8 нульмерных граней (вершин), 12 одномерных граней (ребер), 6 двумерных граней и 1 трехмерная грань — он сам.
Поставим задачу: дан n-мерный куб. Определим количество k-мерных граней у этого куба, где k изменяется от 0 до n и найдём их сумму. Будет получен интересный результат.
Всякая вершина n-мерного куба имеет свои координаты (a1, a2, a3 . an), где a1, a2, a3, . an это 0 или 1. 0 и 1 мы взяли для удобства, также можно взять любые два других числа.
Задачу мы будем решать по индукции:
1. K 0-мерный куб, который имеет одну 0-мерную грань.
1-мерный куб имеет две 0-мерные грани и одну 1-мерную грань.
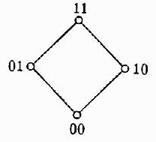
3. 2-мерный куб имеет четыре 0-мерные грани, четыре 1-мерных, одну 2-мерную. Причём, если точки лежат на 1-мерной грани, у них совпадает 1 координата.
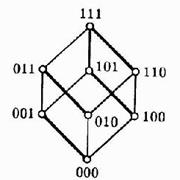
4. 3-мерный куб имеет восемь 0-мерных, двенадцать 1-мерных, шесть 2-мерных граней и одну 3-мерную грань (он сам). Если две точки лежат на одном ребре, у них совпадают 2 координаты, а если они лежат на 2-мерной грани, у них совпадает 1 координата.
Таким образом, в n-мерном кубе точки лежат на k-мерной грани, если у них совпадает k координат из n.
Первый пункт, который нам надо выяснить: сколько 0-мерных граней у n-мерного куба.
Любая вершина имеет свои координаты — a1,a2,a3,a4. an. На каждое место можно подставить 0 или 1 (всего 2 случая на место), поскольку координат n, то случаев 2n.
Рассмотрим количество 1-мерных граней у n-мерного куба (n-1 общая координата).
В подчеркнутом столбце находятся несовпадающие координаты, но он может быть не только последним (n-ым), но и (n-1), (n-2). 1(всего n случаев).
Рёбер — 
У 2-мерной грани n-2 общие координаты. Сколькими способами можно выбрать 2 несовпадающие координаты? — 
случаями. Мы получаем формулу: 
.
У 3-мерной грани n-3 общие координаты. Формула — 
.
Мы пришли к формуле, по которой можно рассчитать количество k-мерных граней у n-мерного куба: 
. Следуя этой формуле, мы составим таблицу, где запишем количество 0,1,2,3,4,5,6,7,8-мерных граней у 0,1,2,3,4,5,6,7,8-мерных кубов.
Кубическое задание функций алгебры логики
Как следует из рассмотренного выше, функция алгебры логики (булева функция) может быть задана:
§ аналитически (системой булевых функций);
§ картами (диаграммами) Венна, Вейча, Карно;
Более компактной формой записи функций алгебры логики является форма, когда вместо полного перечисления всех конъюнкций (дизъюнкций) используют номера наборов, на которых функция принимает единичное значение. Так, например, форма записи f(x1x2x3)=V F(0,2,3) означает, что функция от трех переменных принимает единичное значение на 0, 2 и 3 наборах таблицы истинности. Такая форма записи называется числовой.
Некоторые методы минимизации ориентируются на задание булевой функции в виде кубического покрытия. При этом логическая функция удобно интерпретируется с использованием ее геометрического представления. Так, функцию двух переменных можно интерпретировать как плоскость, заданную в системе координат х1х2. Получится квадрат, вершины которого соответствуют комбинациям переменных. Для геометрической интерпретации функции трех переменных используется куб, заданный в системе координат х1х2х3 .
Новое представление булевой функции получается путем отображения булевой функции n переменных на n-мерный куб (n-куб).
Для отображения булевой функции n переменных на n-кубе устанавливается соответствие между членами СДНФ и вершинами n-куба. На n-кубе определим координатную систему с координатами (e1. en), ei=0,1.
Установим соответствие между членом СДНФ x1 e1 x2 e2 . xn en и некоторой вершиной e1,e2, . en куба. При этом xi ei = xi, если ei=1, и xi ei = xi, если ei=0.
 |
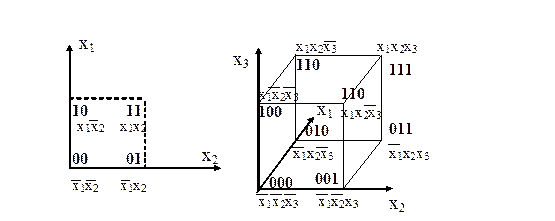Рис.23. Геометрическое представление функции двух и трех переменных
Каждый набор при кубическом задании ФАЛ называется кубом.
Как следует из таблицы истинности (табл. 14), функция f определена на трех группах наборов переменных: L=<3,4,5,6,7>, D= <0,2>и N=<1>.
Конъюнкции максимального ранга (конституенты единицы) принято называть 0-кубами. Множество 0-кубов образуют кубический комплекс
| Таблица 14 | |||
| х1 | х2 | х3 | f |
| — |
011
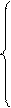
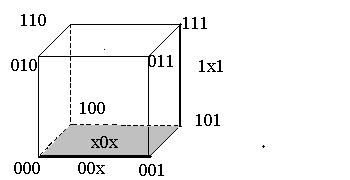
Над 0-кубами, кодовое расстояние которых равно 1, выполняется операция склеивания, в результате которой образуются новые кубы, содержащие свободные координаты. Свободная (независимая) координата может принимать как нулевое, так и единичное значение, остальные компоненты называются связанными. Куб, содержащий свободные координаты, покрывает кубы, на которых он образован. Куб с одной независимой координатой х называется кубом первой размерности и в геометрическом представлении это ребро, покрывающее обе вершины. Кубы, образующиеся в результате последовательного выполнения операции склеивания, назовем r-кубами, где r – размерность полученного куба.
Геометрическая интерпретация сказанного приведена на рис. 24. В результате склеивания кубов 101 и 111 (0-кубы, вершины) образован 1-куб 1×1 (ребро), а 1-кубов 00x и 10х — 2-куб х0х (грань). Рис. 24. Образование новых кубов Кубическое представление ФАЛ позволяет обойтись тремя переменными 0,1,х вместо х1, х2. хn . Количество свободных координат в кубе определяет его размерность r, чем i-го куба. больше r, тем больше свободных координат и тем меньше входов будет иметь реализующая его схема (логический элемент). Цена схемы определяется количеством входов элементов, используемых для ее реализации: где k − количество полученных кубов; n-ri − количество единичных и нулевых значений Два r-куба могут образовать r+1-куб, если в этих r-кубах все координаты, в том числе и свободные, совпадают, за исключением лишь какой-либо одной, которая в этих кубах имеет противоположное значение.
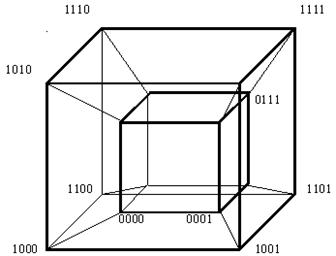
На рис. 25 приведено изображение куба, соответствующего булевой функции от четырёх переменных (гиперкуб). Рис. 25. Геометрическое представление функции четырех переменных Как следует из рисунка, геометрическое представление 4-куба уже довольно сложное. Поэтому для функций, зависящих более чем от четырёх переменных, предпочтительным является аналитическое представление булевых функций. Метод Квайна −Мак-Класки Этот метод ориентирован на числовое задание ФАЛ в виде кубического комплекса, состоящего из 0-кубов. Метод представляет собой формализованный на этапе нахождения простых импликант метод Квайна. Основной недостаток метода Квайна – необходимость выполнения полного сравнения (склеивания) всех первичных импликант. В случае большого их количества сложность этого сравнения существенно возрастает. В рассматриваемом методе все исходные n-кубы разбиваются на непересекающиеся подгруппы по количеству единиц в кубе. Пусть, например, задана функция Сформируем кубический комплекс K, состоящий из 0-кубов: K=(0010, 0011, 0100, 0110, 1001, 1010, 1011, 1100). Выполнив разбиение комплекса K на группы, получим: Попарное сравнение можно проводить только между соседними по номеру группами кубов, так как кубы, порождающие новые кубы, должны иметь кодовое расстояние, равное 1. В результате сравнения кубов получим: После выполнения первого шага алгоритма простых импликант не выявлено. Полученные 1-кубы разобьем на n групп кубов в зависимости от местоположения свободной координаты в кубе. Далее выполняется сравнение кубов внутри каждой из групп. В результате могут быть получены 2-кубы, которые, в свою очередь, аналогично 1-кубам будут объединены в группы по совпадению свободных координат и вновь будет выполнено сравнение. На каждом шаге сравнения выявляются кубы, не участвовавшие в образовании новых кубов, и исключаются из дальнейшего упрощения. Для рассматриваемого примера сравнение в группах Дальнейшее сравнение не приводит к формированию новых кубов Далее аналогично методу Квайна строится импликантная таблица (табл.15). Формирование минимального покрытия сводится к выявлению обязательных простых импликант и построению на их основе тупиковых форм.
Из таблицы следует, что простые импликанты x100, 10×1, x01x являются обязательными. Оставшиеся две простые импликанты не являются обязательными и образуют следующие две тупиковые формы. Булев куб
По определению, булев куб размерности n есть множество В n =< |xk=0,1; k=1,2,…,n>. Элементы (точки) булева куба принять записывать в виде последовательности нулей и единиц, без запятых и скобок: x1x2…xn. ê Булев куб является частично упорядоченным множеством: a ´ b Ç аi ≤ bi для всех i=1,n. ê Вектора 0 = (0, …,0) и 1= (1,…,1) являются наименьшим и наибольшим элементами куба. ê Этот порядок будем называть булевым порядком. ê Булев куб с таким упорядочиванием является полной дистрибутивной решёткой. ê Полная дистрибутивная решётка в то же время является и алгеброй типа . Алгеброй Буля называется алгебра, операции которой удовлетворяют следующим свойствам:
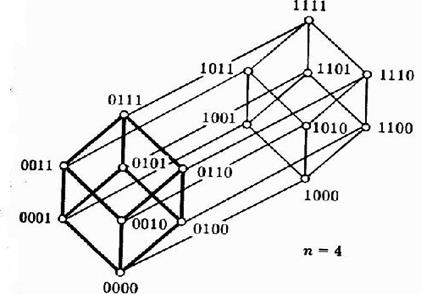
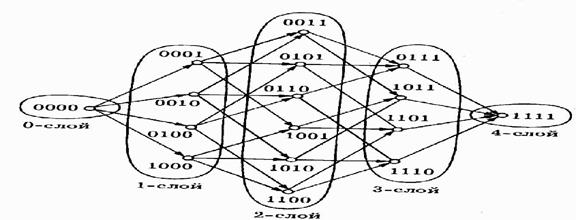
ê Простейшая алгебра Буля B = (B; Ú, Ù, ) имеет носителем двухэлементное множество B=<0,1>, <Л, И> ê n–мерный булев куб является алгеброй B n = (B n ; Ú, Ù, , 0,1). ê n–мерный булев куб является полной дистрибутивной решёткой. ê Алгебру B n можно интерпретировать как векторное пространство над полем (B; Ú, Ù). ê Алгебра B n изоморфна алгебре (2 U ;Ç,È,¯,Æ,U) с n–элементным множеством U. Точки булева куба представляются последовательностью (словом) длины n. Интерпретация этого слова как двоичного числа является нумерацией и, следовательно, задаёт на кубе линейный порядок, отличный от булева. Будем его называть числовым порядком. n-мерный булев куб состоит из 2 n элементов. Конечное число точек всегда можно изобразить на плоскости – т.е. булев куб произвольной размерности можно изображать графически. n=0 n=1. – Двухэлементное множество, диаграмма Хассе которого имеет вид: n=2. Булев квадрат имеет четыре элемента, изображаемые диаграммой: n=3. Трёхмерный булев куб изображается следующим образом: n=4. Четырёхмерный куб можно изобразить следующим образом:
Этот же куб часто изображают в виде ориентированной сети. Линии сети соединяют элементы куба, находящиеся в отношении доминирования, а каждый слой (уровень) сети состоит из элементов антицепи.
Грани булева куба. Если в определении булева куба, т.е. множества всех двоичных векторов длины n, зафиксировать некоторую компоненту, скажем, k-ую, мы получим множество из 2 n-1 элементов, которое будет изоморфно кубу размерности n–1. Это множество называется подкубом, или гранью, размерности n–1. На подкубе индуцируется частичный порядок. Номер зафиксированной компоненты называется направлением грани. Всего можно зафиксировать n различных компонент – говорят об n способах вложения или о соответствующем числе граней. Продолжая процедуру фиксации компонент куба k раз, получим грань (подкуб) размерности n–k, номера зафиксированных компонент 1≤i1 detector |
,
, 
, 
.
, 
.
, 
, 
, 
.
… 
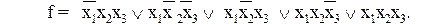
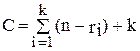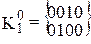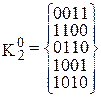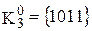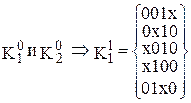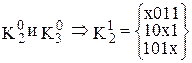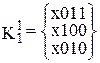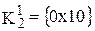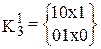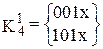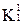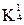привело к образованию двух новых кубов х01х и х01х и кубов, не образовавших новых <х100, 0х10, 10х1, 01х0>.
, 
.
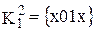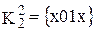