Загадки трех точек
Построение сечения куба по трем точкам.
Скачать:
Предварительный просмотр:
Подписи к слайдам:
« Загадка трёх точек» Информационно-исследовательский проект
Цели проекта: построение сечений в кубе, проходящих через три точки; составление задач по теме « Сечение куба плоскостью»; оформление презентации; подготовка выступления.
В геометрии нет царской дороги Евклид
Аксиомы стереометрии Через любые три точки пространства, не лежащие на одной прямой, проходит единственная плоскость.
Для решения многих геометрических задач, связанных с кубом полезно уметь строить на рисунке их сечения различными плоскостями. Под сечением будем понимать любую плоскость (назовем ее секущей плоскостью), по обе стороны от которой имеются точки данной фигуры. Секущая плоскость пересекает многогранник по отрезкам. Многоугольник, который будет образован этими отрезками, и является сечением фигуры.
Правила построения сечений многогранников: 1) проводим прямые через точки, лежащие в одной плоскости; 2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого: а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости); б) параллельные грани плоскость сечения пересекает по параллельным прямым.
Куб имеет шесть граней. Его сечением могут быть : треугольники, четырехугольники, пятиугольники, шестиугольники.
Рассмотрим построение этих сечений.
Полученный треугольник EFG будет искомым сечением . Построить сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба .
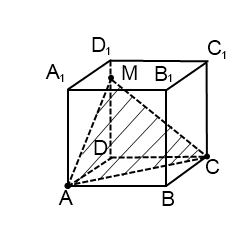
Построить сечение куба плоскостью, проходящей через точки A, C и M.
Для построения сечения куба, проходящего через точки лежащие на ребрах куба, выходящих из одной вершины, достаточно просто соединить данные точки отрезками . В сечении получится треугольник.
Построить сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба.
Полученный прямоугольник BCFE будет искомым сечением. Построить сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба, для которых AE = DF . Решение. Для построения сечения куба, проходящего через точки E , F , G , соединим точки E и F . Прямая EF будет параллельна AD и, следовательно, BC . Соединим точки E и B , F и C .
Построить сечение куба плоскостью, проходящей через точки E , F , лежащие на ребрах куба и вершину B . Решение. Для построения сечения куба, проходящего через точки E , F и вершину B , Соединим отрезками точки E и B , F и B . Через точки E и F проведем прямые, параллельные BF и BE , соответственно.
Полученный параллелограмм BFGE будет искомым сечением Построить сечение куба плоскостью, проходящей через точки E , F , лежащие на ребрах куба и вершину B . Решение. Для построения сечения куба, проходящего через точки E , F и вершину B , Соединим отрезками точки E и B , F и B . Через точки E и F проведем прямые, параллельные BF и BE , соответственно.
Плоскость сечения параллельна одному из ребер куба или проходит через ребро (прямоугольник) Плоскость сечения пересекает четыре параллельных ребра куба (параллелограмм)
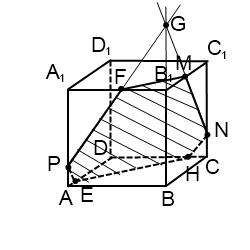
Полученный пятиугольник EFSGQ будет искомым сечением Построить сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба. Решение. Для построения сечения куба, проходящего через точки E , F , G , проведем прямую EF и обозначим P её точку пересечения с AD . Обозначим Q , R точки пересечения прямой PG с AB и DC . Обозначим S точку пересечения FR c СС 1. Соединим точки E и Q , G и S .
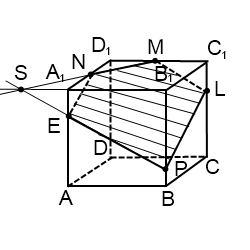
Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1). Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый). Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую. Пятиугольник MNLPS — искомое сечение .
В сечении куба плоскостью может получится только тот пятиугольник, у которого имеются две пары параллельных сторон.
Построить сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба. Решение. Для построения сечения куба, проходящего через точки E , F , G , найдем точку P пересечения прямой EF и плоскости грани ABCD . Обозначим Q , R точки пересечения прямой PG с AB и CD . Проведем прямую RF и обозначим S , T её точки пересечения с CC 1 и DD 1. Проведем прямую TE и обозначим U её точку пересечения с A 1 D 1. Соединим точки E и Q , G и S , F и U . Полученный шестиугольник EUFSGQ будет искомым сечением .
В сечении куба плоскостью может получится только тот шестиугольник, у которого имеется три пары параллельных сторон.
Дано: M€AA1 , N€B1C1,L€AD Построить: ( MNL)
Сечение геометрия точки в кубе
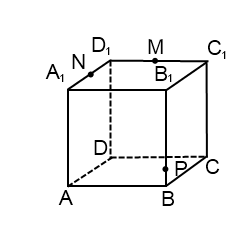
Постройте сечение куба, проходящее через точки M, N и P. Определите вид треугольника, являющегося сечением.
Точки M и N лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, тогда соединяем M и N сплошной линией. Аналогично строим прямую NP. Точки P и M лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок PM. Он невидимый, тогда соединяем P и N штрихом. Треугольник MNP — искомое сечение.
Так как это куб, то треугольник, являющийся сечением — равносторонний.
Постройте сечение куба, проходящее через точки M, N и P. Определите вид треугольника, являющегося сечением.
Постройте сечение куба, проходящее через точки M, N и P. Определите вид треугольника, являющегося сечением.
Точки M и N лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он невидимый, тогда соединяем M и N штрихом. Аналогично строим прямую MP. Точки P и N лежат в одной плоскости, следовательно, через них можем провести прямую. След этой прямой — отрезок PN. Он видимый, тогда соединяем P и N сплошной линией. Треугольник MNP — искомое сечение.
Так как это куб, то треугольник, являющийся сечением — равнобедренный остроугольный.
Узнать ещё
Знание — сила. Познавательная информация
Сечение куба плоскостью
Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
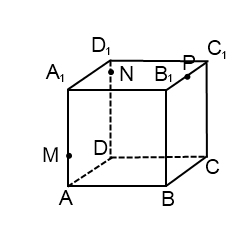
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
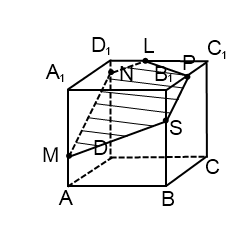
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
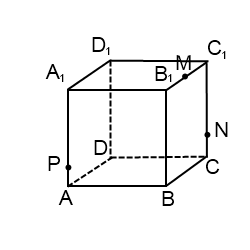
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
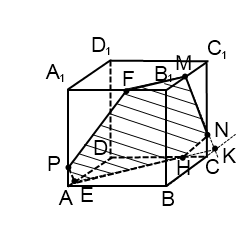
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
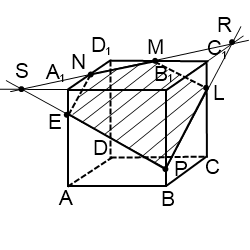
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.
Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
Учимся строить сечения многогранников. Часть 2.
Учимся строить сечения многогранников. Часть 2.
Эта статья для тех, кто хочет научиться строить сечения. Она содержит 11 заданий для построения сечений, подсказки и ответы к каждому заданию. Рекомендую сначала прочитать эту статью и посмотреть это видео.
Вспомним, что сечение многогранника плоскостью представляет собой плоский многоугольник, вершины которого принадлежат сторонам, а ребра — граням многогранника. Две соседние вершины принадлежат одной грани многогранника.
Чтобы найти точку, лежащую одновременно в двух плоскостях, нужно найти точку пересечения прямой, лежащей в первой плоскости, с прямой, лежащей во второй плоскости.
В подсказках и ответах изображение дополнительных прямых, используемых при построении сечения, сплошными линиями или пунктирными, не зависит от того, видимы эти прямые или нет.
Рядом с каждой дополнительной прямой указан ее порядковый номер при построении сечения. Все прямые проведены через две точки, принадлежащие определенной плоскости. Прямые пронумерованы в порядке их построения. Рекомендуется при использовании подсказки и воспроизведении построения сечения проговаривать, какой плоскости принадлежит данная прямая, каким плоскостям принадлежит точка их пересечения.
Постройте сечения, проходящие через точки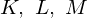 
.
Задание 1:
Сечение геометрия точки в кубе
Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
Примеры построения сечений:
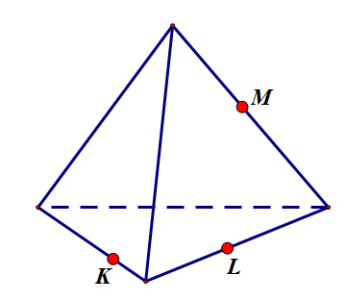
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.
Соединим точки M и L, лежащие в плоскости AA1D1D.
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2;
пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;
Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3 , которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.
Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.
.
Соединим точки M и L, лежащие в плоскости AA1D1D.
.
Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.
.
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
.
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
.
Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).
.
Соединим точки P и L ( они лежат в одной плоскости).
.