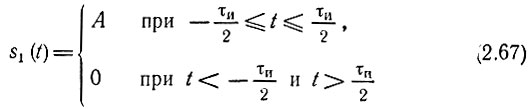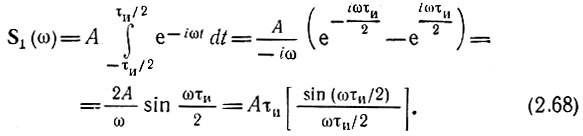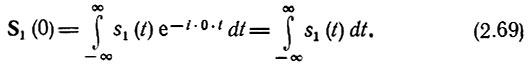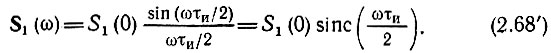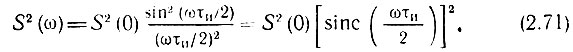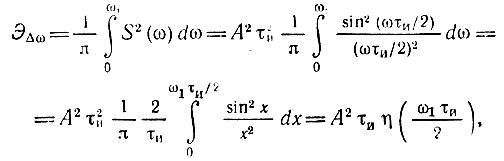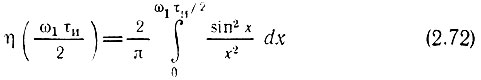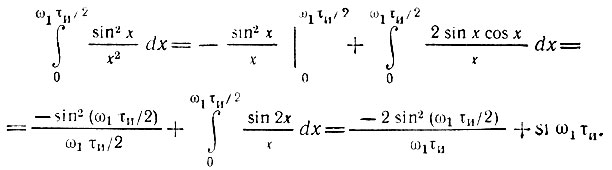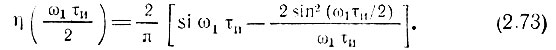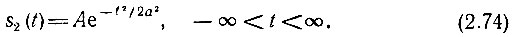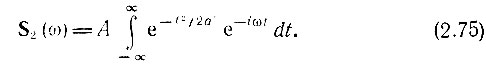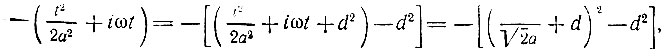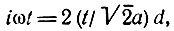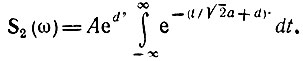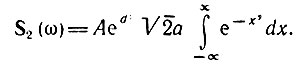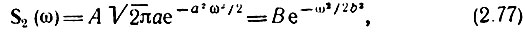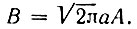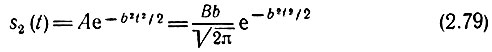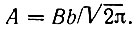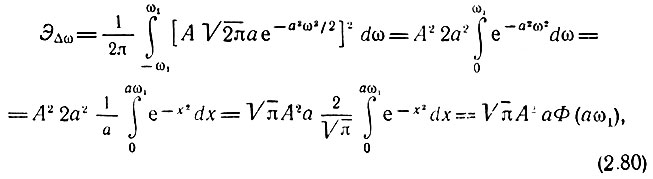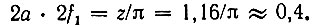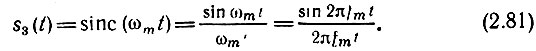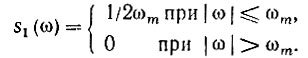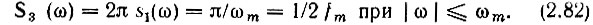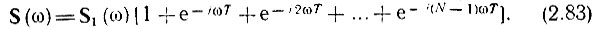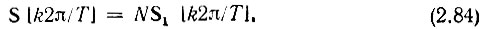Рассчитать спектральную плотность импульса

Спектральная плотность прямоугольного видеоимпульса

Най­дём спек­траль­ные ха­рак­те­ри­сти­ки (ам­пли­туд­ную и фа­зо­вую) оди­ноч­но­го пря­мо­уголь­но­го им­пуль­са, опи­сы­ва­е­мо­го вы­ра­же­ни­ем:

Гра­фи­че­ское изоб­ра­же­ние им­пуль­са пред­став­ле­но на ри­сун­ке.

При­ме­няя фор­му­лу (4.1), на­хо­дим спек­траль­ную плот­ность:

За­ме­тим, что про­из­ве­де­ние U₀τ , рав­ное пло­ща­ди им­пуль­са, опре­де­ля­ет зна­че­ние спек­траль­ной плот­но­сти им­пуль­са при ω = 0 , т. е. S(0) = U₀τ . Бо­лее то­го, это вы­ра­же­ние спра­вед­ли­во для им­пуль­сов про­из­воль­ной фор­мы:

Спектр ам­пли­туд оди­ноч­но­го пря­мо­уголь­но­го им­пуль­са пред­став­ля­ет из се­бя мо­дуль вы­ра­же­ния (4.10):

Гра­фи­че­ски спектр ам­пли­туд это­го им­пуль­са пред­став­лен на ри­сун­ке (при­ве­де­на пра­вая часть спек­траль­ной ха­рак­те­ри­сти­ки, со­от­вет­ству­ю­щая по­ло­жи­тель­ным зна­че­ни­ям ω ).

Из ри­сун­ка и ана­ли­за со­от­но­ше­ния (4.12) сле­ду­ет, что при уве­ли­че­нии дли­тель­но­сти им­пуль­са τ рас­сто­я­ние меж­ду ну­ля­ми функ­ции S(ω) со­кра­ща­ет­ся, что рав­но­силь­но суже­нию спек­тра ам­пли­туд. При этом зна­че­ние S(ω) при ω = 0 воз­рас­та­ет. При уко­ра­чи­ва­нии (сжа­тии) им­пуль­са рас­сто­я­ние меж­ду ну­ля­ми функ­ции S(ω) , на­про­тив, уве­ли­чи­ва­ет­ся (спектр рас­ши­ря­ет­ся), а зна­че­ние S(0) убы­ва­ет. В пре­де­ле при τ → 0 зна­че­ние ω = ±2π/T стре­мит­ся к бес­ко­неч­но­сти, а мо­дуль спек­траль­ной плот­но­сти, бес­ко­неч­но ма­лый по ве­ли­чи­не при по­сто­ян­ном зна­че­нии U₀ , ста­но­вит­ся рав­но­мер­ным в по­ло­се ча­стот от –∞ до ∞ . Оче­вид­но так­же, что ам­пли­туд­ный спектр пря­мо­уголь­но­го им­пуль­са име­ет ту же фор­му, что и оги­ба­ю­щая пе­ри­о­ди­че­ской по­сле­до­ва­тель­но­сти та­ких им­пуль­сов.

Фа­зо­вая ха­рак­те­ри­сти­ка спек­тра пря­мо­уголь­но­го им­пуль­са (спектр фаз) опи­сы­ва­ет­ся вы­ра­же­ни­ем: , n = 0, ± 1, ± 2, . Оче­вид­но, что каж­дое из­ме­не­ние зна­ка S(jω) учи­ты­ва­ет­ся из­ме­не­ни­ем фа­зы на π .

Источник

Спектральная плотность экспоненциального импульса

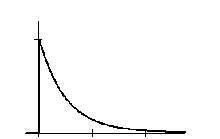
Найдем спектральную плотность экспоненциального импульса (рис. 2.17, а):

(2.32)

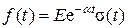
путем непосредственного применения преобразования Фурье:

. (2.33)

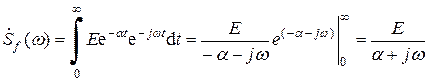
Получившееся выражение является существенно комплексным. Это объясняется тем, что рассматриваемый экспоненциальный импульс не является ни четной, ни нечетной функцией. Чтобы построить график спектральной плотности, нужно вычислить ее модуль:

. (2.34)

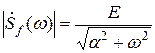
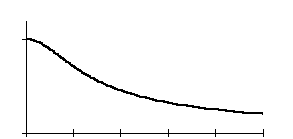
График модуля спектральной плотности экспоненциального импульса изображен на рис. 2.17, б. Экспоненциальный импульс имеет вертикальный передний фронт, и поэтому его спектральная плотность убывает с ростом частоты медленно, пропорционально 1/w.

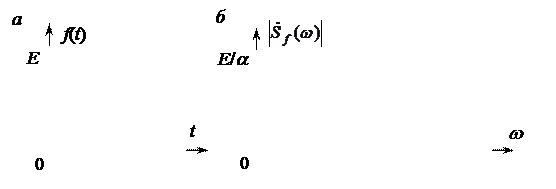Рис. 2.17. Экспоненциальный импульс (а) и график модуля

Источник

Спектральная плотность треугольного импульса

Найдем спектральную плотность треугольного импульса, изображенного на рис. 2.15, а. Ее можно вычислить путем непосредственного применения преобразования Фурье (2.12), однако это несколько громоздко, так как получающиеся при этом интегралы приходится вычислять по частям. Значительно проще и изящнее оказывается метод, основанный на применении теорем о спектрах.

Продифференцируем треугольный импульс один раз (рис. 2.15, б) и затем еще один раз (рис. 2.15, в). Получающийся при этом сигнал состоит из трех
d-функций, причем каждая из них умножается на высоту соответствующего скачка первой производной исходного сигнала:

. (2.28)

Зная спектральную плотность d-функции и используя теорему о запаздывании, запишем выражение для спектральной плотности второй производной треугольного импульса:

(2.29)

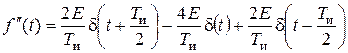
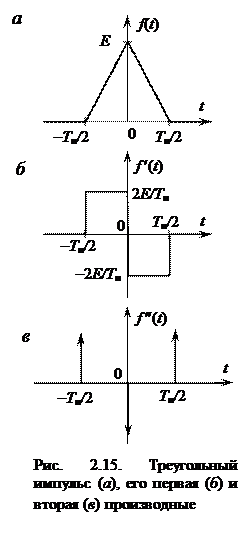
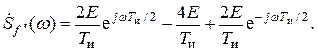
Используя формулу Эйлера, получаем:

.

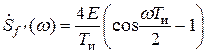
Чтобы определить искомую спектральную плотность треугольного импульса, нужно спектральную плотность второй производной разделить на (jw) 2

. (2.30)

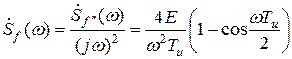
Преобразуем выражение (2.30) к виду, более удобному для анализа:

. (2.31)

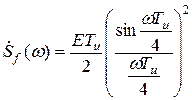
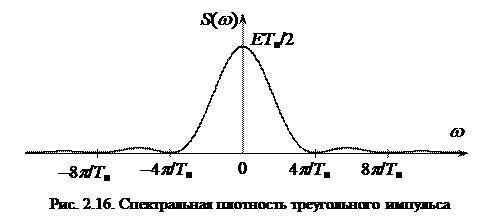
График спектральной плотности треугольного импульса изображен на рис. 2.16.

По сравнению со спектральной плотностью прямоугольного импульса спектральная плотность треугольного импульса имеет более низкий уровень боковых лепестков: первый лепесток равен 0,04 от максимума по сравнению с 0,2 для прямоугольного импульса, и с повышением частоты уровень боковых лепестков убывает как 1/w 2 (для прямоугольного импульса – как 1/w). Это объясняется тем, что треугольный импульс имеет более гладкий характер, чем прямоугольный, в нем отсутствуют вертикальные фронты, для формирования которых нужен достаточно высокий уровень высокочастотных составляющих спектра.

Источник

Рассчитать спектральную плотность импульса

2.9. Примеры определения спектров непериодических колебаний

Основной задачей настоящего параграфа является пояснение свойств преобразований Фурье, приведенных в предыдущих параграфах, на примерах, важных для практики.

1. Импульс прямоугольной формы

Простейшее колебание, определяемое выражением

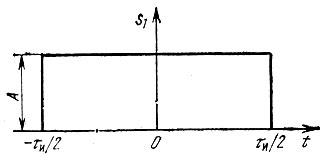
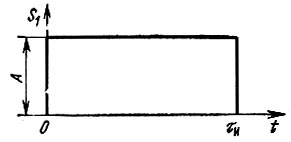
и представленное на рис. 2.13, получило широкое распространение как в технике, так и в теории сигналов и цепей. Применяя формулу (2.48), находим спектральную плотность (рис. 2.14)

Рис. 2.13. Импульс прямоугольной формы

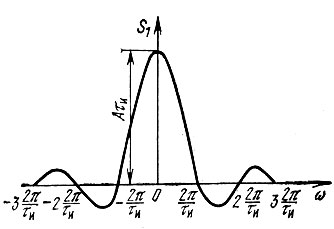
Рис. 2.14. Спектральная плотность прямоугольного импульса

Заметим, что произведение Аτ_и, равное площади импульса, определяет значение спектральной плотности импульса при ω = 0, т. е. S₁(0) = Аτ_и. Этот вывод можно распространить на импульс произвольной формы.

Действительно, из общего выражения (2.48) следует, что

Правая часть этого выражения есть не что иное, как площадь импульса s₁(t). Таким образом, выражение (2.68) можно записать в форме

Здесь через sinc(ωτ_и/2) обозначена функция

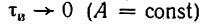
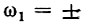
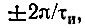
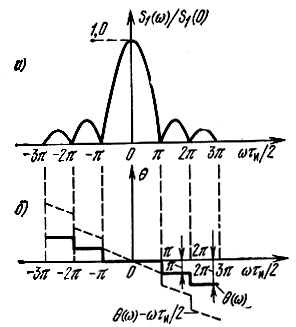
При удлинении (растягивании) импульса расстояние между нулями функции S₁(ω) сокращается, что равносильно сужению спектра. Значение S₁(0) при этом возрастает. При укорочении (сжатии) импульса, наоборот, расстояние между нулями функции S₁(ω) увеличивается (расширение спектра), а значение S₁(0) уменьшается. В пределе при точки соответствующие двум первым нулям функции Sx (со), удаляются в бесконечность и спектральная плотность, бесконечно малая по величине, становится равномерной в полосе частот от -∞ до ∞.

На рис. 2.15 показаны отдельно графики модуля S₁(ω), отнесенного к величине S₁(0), и аргумента θ(ω) спектральной плотности. Первый из этих графиков можно рассматривать как амплитудную, а второй — как фазовую характеристику спектра прямоугольного импульса. Каждая перемена знака S₁(ω) учитывается на рис. 2.15, б приращением фазы на π.

Рис. 2.15. Модуль (а) и аргумент (б) спектральной плотности прямоугольного импульса

При отсчете времени не от середины импульса (как на рис. 2.13), а от фронта (рис. 2.16) фазовая характеристика спектра импульса должна быть дополнена слагаемым ωτ_и/2, учитывающим сдвиг импульса на время τ_и/2 (в сторону запаздывания). Результирующая фазовая характеристика принимает при этом вид, показанный на рис. 2.15, б штриховой линией.

Рис. 2.16. Совмещение начала отсчета времени с фронтом прямоугольного импульса

Рассмотрим вопрос о распределении энергии в спектре импульса. В соответствии с § 2.8 и формулой (2.68′) спектральная плотность энергии прямоугольного импульса

С помощью равенства Парсеваля нетрудно вычислить энергию в заданной полосе частот.

Пусть нас интересует полоса Δω от -ω₁ до ω₁. Тогда по формуле (2.66) находим энергию в указанной полосе

где A 2 τ_и = Э есть полная энергия импульса, а функция

определяет относительную долю энергии в полосе частот от 0 до ω₁.

Интеграл, входящий в выражение (2.72), с помощью интегрирования по частям может быть приведен к виду

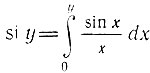
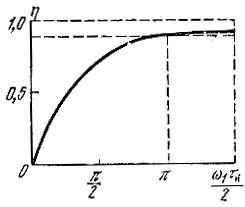
Здесь — интегральный синус.

График функции η(ω₁τ_и/2) изображен на рис. 2.17. Из этого рисунка видно, что при ω₁τ_и/2 = π, т. е. при f₁τ_и = 1, в полосе частот от 0 до f₁ = 1/τ_и сосредоточено около 90% всей энергии импульса. На основе формулы (2.73) можно выбирать полосу пропускания цепи (фильтра) по заданному коэффициенту использования энергии импульса. Следует, однако, подчеркнуть, что в тех случаях, когда требуется получить на выходе фильтра форму импульса, близкую к прямоугольной, величина произведения f₁τ_и должна быть гораздо больше единицы.

Рис. 2.17. Доля энергии прямоугольного импульса в полосе частот 0, ω₁

2. Колоколообразный (гауссов) импульс

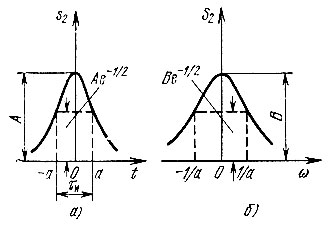
Представленный на рис. 2.18, а импульс определяется выражением

Рис. 2.18. Колоколообразный (гауссов) импульс (а) и его спектральная плотность (б)

Этот импульс, совпадающий по форме с графиком нормального (гауссова) закона распределения вероятностей, называется также «гауссовым импульсом». Постоянная а имеет смысл половины длительности импульса, определяемой на уровне e 1 /₂ = 1/е 1 /₂ = 0,606 от амплитуды импульса. Таким образом, полная длительность импульса τ_и равна 2а.

Применяя выражение (2.48), получаем

Для вычисления интеграла удобно в подынтегральной функции дополнить показатель степени до квадрата суммы

где величина d определяется из условия

Таким образом, выражение (2.75) можно привести к виду

Переходя к новой переменной 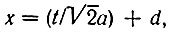получаем

Учитывая, что входящий в это выражение интеграл равен 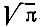окончательно получаем

График этой функции изображен на рис. 2.18, б.

Полученный результат имеет важное значение для теории сигналов. Оказывается, что гауссов импульс и его спектр выражаются одинаковыми функциями и обладают свойством симметрии: для получения одной из них по заданной другой достаточно заменить t на ω. При этом спектральная полоса, определяемая на уровне е 1 /₂ от максимального значения, равна 2b = 2/а = 2⋅2/τ_и = 4/τ_и, а коэффициент

соответствует гауссов импульс

с длительностью 2/b и амплитудой

Очевидно, что чем меньше длительность импульса τ_и, тем шире спектральная полоса 2b.

Вычислим энергию, содержащуюся в полосе частот Δω от -ω₁ до ω₁. Основываясь на формуле (2.77), находим

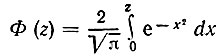
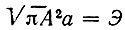
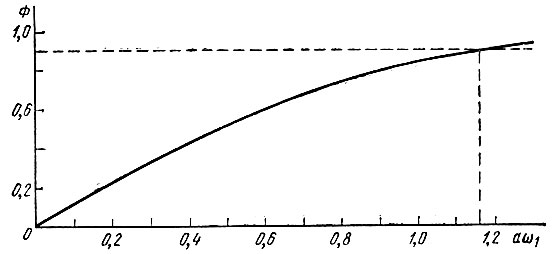
где — интеграл вероятности, а — полная энергия колоколообразного импульса.

Таким образом, отношение энергии в полосе частот от -ω₁ до ω₁ к полной энергии гауссова импульса равно Φ(аω₁).

Функция Φ(z) табулирована, график ее показан на рис. 2.19. Для получения 90% энергии импульсу требуется z = aω₁ ≈ 1,16 или произведение полной длительности импульса 2а на 2f₁ равное

Рис. 2.19. Доля энергии гауссова импульса в полосе частот 0, ω₁

3. Импульс вида sinc(x)

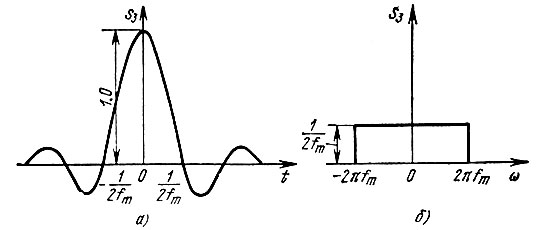
На рис. 2.20, а изображен импульс, определяемый выражением

Рис. 2.20. Импульс вида sinc(ω_mt) (а) и его спектральная плотность (б)

Вместо вычисления спектральной плотности по формуле (2.48) воспользуемся результатами примера 1 данного параграфа и свойством взаимной заменимости ω и t в преобразованиях Фурье для четных функций времени (см. п. 7, § 2.7).

Из рисунков 2.13 и 2.14 очевидно, что после замены ω на t и t на ω заданной функции s₃(t) будет соответствовать спектр прямоугольной формы. Для применения преобразования (2.65) нужно сначала пронормировать функцию S₁ω на рис. 2.14 таким образом, чтобы максимальное ее значение S₁(0) равнялось единице (как и s₃(t) = s₃(0) на рис. 2.20, а). Приравняв Aτ_и = 1, получим амплитуду импульса s₁(t) на рис. 2.13, равную 1/τ_и. Заменив далее t на ω, τ_и/2 на ω_m и амплитуду импульса 1/τ_и на 1/2ω_m, получим спектральную функцию

Применяя формулу (2.65), находим искомую спектральную плотность

График S₃(ω) представлен на рис. 2.20, б.

4. Группа одинаковых и равноотстоящих импульсов

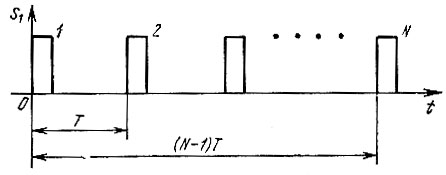
Спектральную плотность первого импульса в пачке (рис. 2.21) обозначим через S₁(ω). Тогда для второго импульса, сдвинутого относительно первого на время Т (в сторону запаздывания), спектральную плотность можно на основании (2.57) представить выражением S₂(ω) = S₁(ω)е -iωT , для третьего импульса S₃(ω) = S₁(ω)е -i2ωT и т. д.

Рис. 2.21. Пачка одинаковых, равноотстоящих импульсов

Для группы из N импульсов в соответствии с принципом линейного суммирования спектров при сложении сигналов получим спектральную плотность

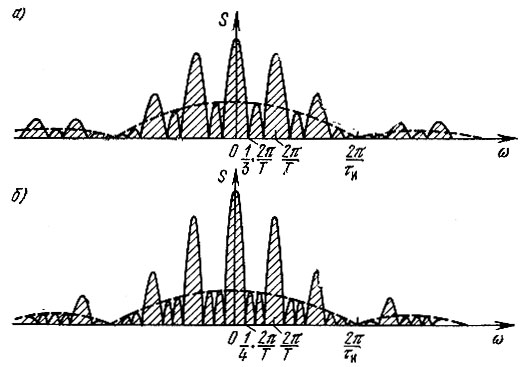
При частотах, отвечающих условию ω = k2π/T, где k — целое число, каждое из слагаемых в квадратных скобках равно единице и, следовательно,

Таким образом, при частотах ω = k2π/Т модуль спектральной плотности пачки в N раз больше модуля спектра одиночного импульса. Это объясняется тем, что спектральные составляющие различных импульсов с указанными выше частотами складываются со сдвигами фаз, кратными 2π.

При частотах же ω = (1/N)(2π/Т), а также при некоторых других частотах, для которых сумма векторов e -ikT обращается в нуль, суммарная спектральная плотность равна нулю. При промежуточных значениях частот модуль S(ω) определяется как геометрическая сумма спектральных плотностей отдельных импульсов.

В качестве иллюстрации на рис, 2.22, а изображен спектр (модуль) пачки из трех прямоугольных импульсов, а на рис. 2.22, б — из четырех, при интервале между соседними импульсами Т = 3τ_и. Штриховыми линиями показана спектральная плотность одиночного импульса. С увеличением числа импульсов в пачке спектральная плотность все более расщепляется и в пределе при N→∞ принимает линейчатую структуру спектра периодической функции.

Рис. 2.22. Модуль спектральной плотности пачки из трех (а) и четырех (б) импульсов

Источник