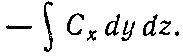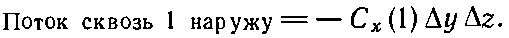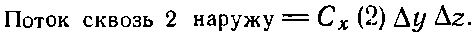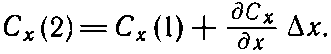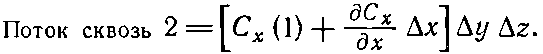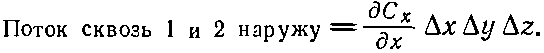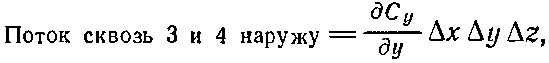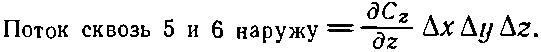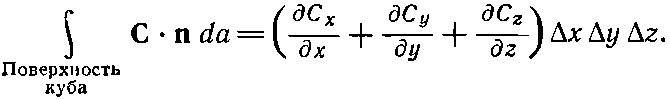- Поток из куба; теорема Гаусса
- § 3. Поток из куба; теорема Гаусса
- Поток вектора напряженности через поверхность куба
- Поток векторного поля: теория и примеры
- Понятие потока векторного поля и его вычисление как поверхностного интеграла
- Направление и интенсивность потока векторного поля
- Вычисление потока векторного поля: примеры
Поток из куба; теорема Гаусса
Рассмотрим теперь частный случай потока из маленького кубика и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно Δx:, ребро куба (а точнее, бруска) в направлении у равно Δу, а в направлении z равно Δz. Мы хотим найти поток векторного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5). Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен
 |
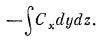Так как куб считается малым, этот интеграл можно заменить значением Сх в центре грани [эту точку мы обозначили (1)], умноженным на площадь грани ΔyΔz:
 |
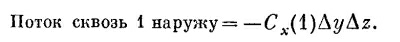Подобным же образом поток наружу через грань 2 равен
 |
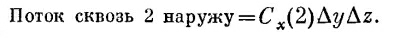Величины Сх(1) и Сх(2), вообще говоря, слегка отличаются. Если Δx достаточно мало, то можно написать
 |
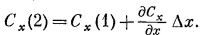Существуют, конечно, и другие члены, но в них входит (Δx) 2 и высшие степени Δx, и в пределе малых Δx ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен
 |
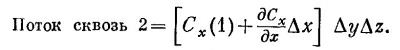Складывая потоки через грани 1 и 2, получаем
 |
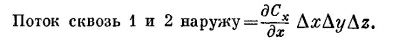Производную нужно вычислять в центре грани 1, т. е. в точке [х, y + (Δy/2), z+(Δz/2)]. Но если куб очень маленький, мы сделаем пренебрежимую ошибку, если вычислим ее в вершине (х, у, z).
Повторяя те же рассуждения с каждой парой граней, мы получаем
 |
А общий поток через все грани равен сумме этих членов. Мы обнаруживаем, что
 |
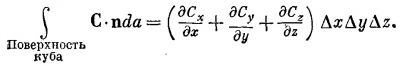Сумма производных в скобках как раз есть v·С, a ΔxΔyΔz=ΔV (объем куба). Таким образом, мы можем утверждать, что для бесконечно малого куба
 |
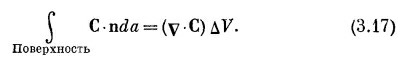Мы показали, что поток наружу с поверхности бесконечно малого куба равен произведению дивергенции вектора на объем куба. Теперь мы понимаем «смысл» понятия дивергенции вектора. Дивергенция вектора в точке Р — это поток С («истечение» С наружу) на единицу объема, взятого в окрестности Р.
Мы связали дивергенцию С с потоком С из бесконечно малого объема. Для любого конечного объема можно теперь использовать факт, доказанный выше, что суммарный поток из объема есть сумма потоков из отдельных его частей. Иначе говоря, мы можем проинтегрировать дивергенцию по всему объему. Это приводит нас к теореме, согласно которой интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности может быть представлен также в виде интеграла от дивергенции вектора по объему, заключенному внутри поверхности. Теорему эту называют теоремой Гаусса.
 |
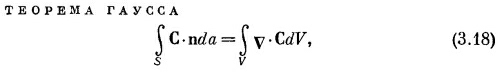где S — произвольная замкнутая поверхность, V — объем внутри нее.
§ 3. Поток из куба; теорема Гаусса
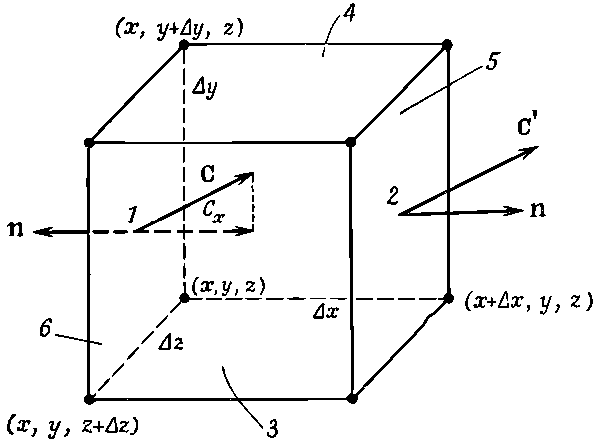
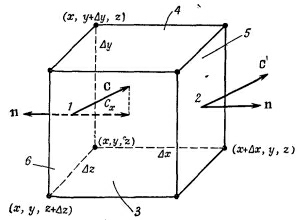
Рассмотрим теперь частный случай потока из маленького кубика[6] и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно ?x, ребро куба (а точнее, бруска) в направлении у равно ?y, а в направлении z равно ?z. Мы хотим найти поток векторного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5).
Фиг. 3.5. Вычисление потока вектора С из маленького кубика.
Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен
Так как куб считается малым, этот интеграл можно заменить значением Сх в центре грани 1эту точку мы обозначили (1), умноженным на площадь грани ?y?z:
Подобным же образом поток наружу через грань 2 равен
Величины Cx(1) и Сх(2), вообще говоря, слегка отличаются. Если ?х достаточно мало, то можно написать
Существуют, конечно, и другие члены, но в них входит (?x) 2 и высшие степени ?x, и в пределе малых ?x ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен
Складывая потоки через грани 1 и 2, получаем
Производную нужно вычислять в центре грани 1, т. е. в точке [x, y+(?y/2), z+(?z/2)]. Но если куб очень маленький, мы сделаем пренебрежимую ошибку, если вычислим ее в вершине (х, у, z).
Повторяя те же рассуждения с каждой парой граней, мы получаем
А общий поток через все грани равен сумме этих членов. Мы обнаруживаем, что
Сумма производных в скобках как раз есть ?·С, а ?x?y?z=?V (объем куба). Таким образом, мы можем утверждать, что для бесконечно малого куба
(3.17)
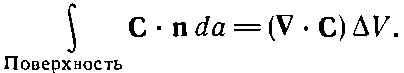
Мы показали, что поток наружу с поверхности бесконечно малого куба равен произведению дивергенции вектора на объем куба. Теперь мы понимаем «смысл» понятия дивергенции вектора. Дивергенция вектора в точке Р — это поток С («истечение» С наружу) на единицу объема, взятого в окрестности Р. Мы связали дивергенцию С с потоком С из бесконечно малого объема. Для любого конечного объема можно теперь использовать факт, доказанный выше, что суммарный поток из объема есть сумма потоков из отдельных его частей. Иначе говоря, мы можем проинтегрировать дивергенцию по всему объему. Это приводит нас к теореме, согласно которой интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности может быть представлен также в виде интеграла от дивергенции вектора по объему, заключенному внутри поверхности. Теорему эту называют теоремой Гаусса.
(3.18)
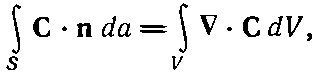
где S — произвольная замкнутая поверхность, V — объем внутри нее.
Поток вектора напряженности через поверхность куба
Куб со стороной а помещен в однородное электрическое поле напряженностью Е. Чему равен поток вектора напряженности через поверхность куба?
Подскажите, я правильно понимаю, что поток будет равен 0 по теор. Гаусса, т.к. нет заряда внутри куба?
Найти поток вектора напряженности через поверхность сферы
Две параллельные бесконечно большие пластины заряжены одинаковыми по величине, но разноименными.
Поток вектора напряженности точечного заряда через поверхность круга
Найти поток вектора напряженности поля точечного заряда q через поверхность круга радиуса R, центр.
Найти поток вектора напряженности электрического поля через одну грань куба
Помогите решить Точечный заряд q = 531 нКл помещен в центре куба с длиной ребра 10 см. Поток.
Чему равен поток вектора напряженности электрического поля через одну грань куба
319. Точечный заряд Q = 1 нКл помещен в центр куба со стороной =1 м. Чему равен поток вектора.
Поток вектора напряженности через куб
Помогите, пожалуйста! Куб помещен в однородное электрическое поле с напряженностью 800 В/м так.
Определение потока вектора напряжённости электрического поля через поверхность сферы
Доброго времени суток! Подскажите, пожалуйста, как решить такую задачу: В целых точках числовой.
Определите поток ФЕ вектора напряженности через эту пластинку, если ее радиус равен r
На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью σ.
Найти поток вектора В через поверхность рамки
Квадратная рамка расположена в одной плоскости с длинным прямым проводником с током 5 А. Сторона.
Поток вектора напряжённости
Добрый день!:) Помогите, плиз с задачкой, не поняла, как её решать. Шар радиусом R=10 см.
Поток векторного поля: теория и примеры
Понятие потока векторного поля и его вычисление как поверхностного интеграла
Своим названием поток векторного поля обязан задачам гидродинамики о потоке жидкости. Поток векторного поля может быть вычислен в виде поверхностного интеграла, который выражает общее количество жидкости, протекающей в единицу времени через некоторую поверхность в направлении вектора скорости течения жидкости в данной точке. Понятие потока векторного поля обобщается также на магнетический поток, поток электричества, поток тепла через заданную поверхность и другие. Поток векторного поля может быть вычислен в виде поверхностного интеграла как первого, так и второго рода и далее мы дадим его вывод через эти интегралы.
Пусть в некоторой области пространства задано векторное поле
и поверхность σ, в каждой точке M которой определён единичный вектор нормали 
. Пусть также направляющие косинусы этого вектора — непрерывные функции координат x, y, z точки M.
Определение потока векторного поля. Потоком W поля вектора 
через поверхность σ называется поверхностный интеграл
Обозначим как a n проекцию вектора на на единичный вектор 
. Тогда поток можем записать как поверхностный интеграл первого рода
поток векторного поля можно вычислить и как поверхностный интеграл второго рода
Направление и интенсивность потока векторного поля
Поток векторного поля зависит от местоположения поверхности σ. Если поверхность размещена так, что во всех её точках вектор поля образует с вектором нормали поверхности острый угол, то проекции вектора a n положительны и, таким образом поток W также положителен (рисунок ниже). Если же поверхность размещена так, что во всех её точках вектор образует с вектором нормали поверхности тупой угол, то поток W отрицателен.
Через каждую точку поверхности проходит одна векторная линия, поэтому поверхность σ пересекает бесконечное множество векторных линий. Однако условно можно принять, что поверхность σ пересекает некоторое конечное число векторных линий. Поэтому можно считать, что поток векторного поля — это число векторных линий, пересекающих поверхность σ. Чем интенсивнее поток векторного поля, тем более плотно расположены векторные линии и в результате получается бОльший поток жидкости.
Если поток векторного поля — поле скорости 
частиц текущей жидкости через поверхность σ, то поверхностный интеграл 
равен количеству жидкости, протекающей в единицу времени через поверхность σ. Если рассматривать магнетическое поле, которое характеризуется вектором магнетической индукции 
, то поверхностный интеграл 
называется магнетическим потоком через поверхность σ и равен общему количеству линий магнетической индукции, пересекающих поверхность σ. В случае электростатического поля интеграл 
выражает число линий электрической силы, пересекающих поверхность σ. Этот интеграл называется потоком вектора интенсивности электростатического поля 
через поверхнсть σ. В теории теплопроводности рассматривается стационарный поток тепла через поверхность σ. Если k — коэффициент теплопроводности, а u(M) — температура в данной области, то поток тепла, протекающего через поверхность σ в единицу времени, определяет интеграл 
.
Вычисление потока векторного поля: примеры
Пример 1. Вычислить поток векторного поля 
через верхнюю сторону треугольника, образованного пересечением плоскости 
с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
1) Поверхностью σ является треугольник ABC , а её проекцией на ось xOy — треугольник AOB .
Координатами вектора нормали данной поверхности являются коэффициенты при переменных в уравнении плоскости:
Из выражения единичного вектора нормали следует, что направляющий косинус 
. Тогда 
.
Теперь можем выразить поток векторного поля в виде поверхностного интеграла первого рода и начать решать его:
Продолжаем вычислять интеграл и, таким образом, поток векторного поля:
Получили ответ: поток векторного поля равен 64.
2) Выражая поток векторного поля через поверхностный интеграл второго рода, получаем
Представим этот интеграл в виде суммы трёх интегралов и каждый вычислим отдельно. Учитывая, что проекция поверхности на ось yOz является треугольник OCB , который ограничивают прямые y = 0 , z = 0 , y + 3z = 6 или y = 6 − 3z и в точках поверхности 2x = 6 − y − 3 , получаем первый интеграл и вычисляем его:
Проекцией поверхности на ось xOz является треугольник OAC , который ограничен прямыми x = 0 , z = 0 , 2x + 3z = 6 или 
. По этим данным получаем второй интеграл, который сразу решаем:
Проекцией поверхности на ось xOy является треугольник OAB , который ограничен прямыми x = 0 , y = 0 , 2x + y = 6 . Получаем третий интеграл и решаем его:
Осталось только сложить все три интеграла:
Получили ответ: поток векторного поля равен 64. Как видим, он совпадает с ответом, полученным в первом случае.
Пример 2. Вычислить поток векторного поля 
через верхнюю сторону треугольника, образованного пересечением плоскости 
с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
Решение. Данная поверхность представляет собой треугольник ABC , изображённый на рисунке ниже.
1) Коэффициенты при x , y и z из уравнения плоскости являются координатами вектора нормали плоскости, которые нужно взять с противоположным знаком (так как вектор нормали верхней стороны треугольника образует с осью Oz острый угол, так что третья координата вектора нормали плоскости должна быть положительной). Таким образом, вектор нормали запишется в координатах так:
единичный вектор нормали (орт):
Скалярное произведение векторного поля и единичного нормального вектора:
Поток векторного поля, таким образом, представим в виде поверхностного интеграла первого рода
Выразим «зет» и продифференцируем то, что уже можно продифференцировать:
2) Представим поток векторного поля в виде поверхностного интеграла второго рода:
Первый и второй интегралы берём со знаком «минус», так как вектор нормали поверхности образует с осями Ox и Oy тупой угол.
Вычисляем первый интеграл:
Вычисляем второй интеграл:
Вычисляем третий интеграл:
Складываем три интеграла и получаем тот же самый результат:
Пример 3. Вычислить поток векторного поля 
через внешнюю сторону параболоида 
в первом октанте, отсечённую плоскостью z = 9 .
Поток векторного поля представим в виде поверхностного интеграла второго рода:
Второй интеграл берём со знаком минус, так как нормальный вектор поверхности образует с осью Oz тупой угол. Вычисляем первый интеграл:
Вычисляем второй интеграл:
В сумме получаем искомый поток векторного поля: