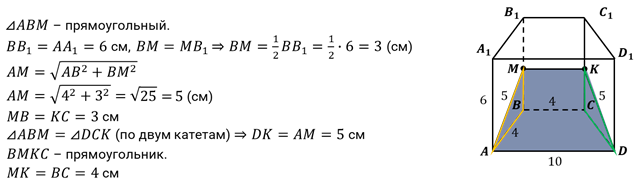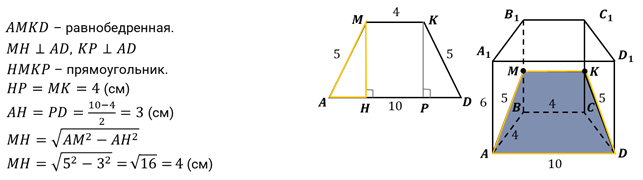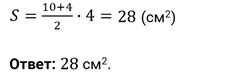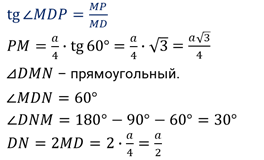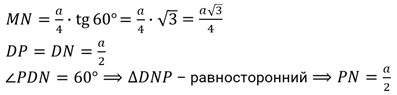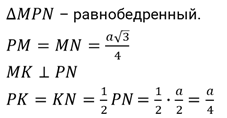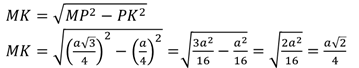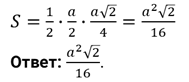Пирамиды призмы кубы 3 класс

5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара

Видеоурок: Объем и площадь поверхности многогранников

Лекция: Объём куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара

Для нахождения объема любого тела необходимо произведение трех параметров тела. Именно поэтому, чтобы проверить правильность решения, следует убедиться в том, что в выведенной Вами формуле оказалось в виде множителя три параметра тела.

Куб

Для нахождения объема куба следует перемножить три стороны. Так как в кубе все они равны, следует просто возвести значение стороны в куб: V = a 3

Прямоугольный параллелепипед

Так как в данной фигуре все углы прямые, то её объем находится просто, как произведение всех сторон: V = abc

Пирамида и конус

Как уже говорилось ранее, эти две фигуры очень похожи. Различие только в том, что у нее разные основания.

Объем пирамиды и конуса находится, как третья произведения площади основания на высоту: V = S_ocH/3

Для пирамиды данная формула изменяется в зависимости от многоугольника, который будет находится в основании.

У конуса же данная формула стандартна, поскольку в его основании лежит окружность: V = πR 2 H/3

Цилиндр

Для нахождения объема цилиндра необходимо найти произведение площади основания на высоту. Так как в основании лежит окружность, получается следующая формула: V = πR 2 H

Не трудно заметить, что формула цилиндра очень похожа на формулу для нахождения объема конуса.

Призма

Как и в нескольких предыдущих случаях, объем призмы находится, как произведение основания на высоту. И не важно, прямая ли эта призма или нет.

Данная формула видоизменяется в зависимости от того, какой многоугольник лежит в основании. Формула очень похожа на формулу нахождения объема пирамиды: V = S_ocH

Шар

Для нахождения объема шара достаточно воспользоваться несложной формулой: V = 4/3*πR 3

Источник

Сечения куба, призмы, пирамиды

Урок 37. Подготовка к ЕГЭ по математике

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока «Сечения куба, призмы, пирамиды»

Для решения большинства задач из раздела стереометрии необходимы знания и навыки в построении сечения объёмных тел. Именно об этом мы сейчас с вами и поговорим.

Итак, секущей плоскостью называют любую плоскость, по обе стороны от которой имеются точки данной фигуры.

Секущая плоскость пересекает грани многогранника по отрезкам.

Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Построить сечение многогранника плоскостью – это значит указать точки пересечения секущей плоскости с рёбрами многогранника и соединить эти точки отрезками, принадлежащими граням многогранника.

Теперь давайте вспомним, что нам необходимо знать для построения плоскости.

Итак, построить плоскость можно: с помощью трёх точек, не лежащих на одной прямой;

с помощью двух пересекающихся прямых;

с помощью прямой и точки, которая не лежит на прямой;

а также с помощью двух параллельных прямых.

Метод следов включает три важных пункта: сначала нужно построить линию пересечения (след) секущей плоскости с плоскостью основания многогранника; затем найти точки пересечения секущей плоскости с рёбрами многогранника, а после этого построить и заштриховать сечение.

В основе построения сечения методом следов лежат две теоремы:

1) если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости;

2) если плоскость проходит через прямую, параллельную другой плоскости, и эти плоскости пересекаются, то линия их пересечения параллельна первой прямой.

Метод вспомогательных сечений применяется при построении сечений в тех случаях, когда неудобно находить след секущей плоскости. Например, след получается очень далеко от заданной фигуры.

Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с методом следов или методом вспомогательных сечений.

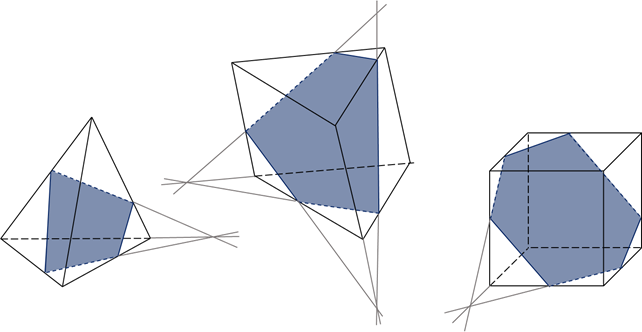
Обратите внимание: тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырёхугольники. А вот параллелепипед имеет шесть граней, поэтому его сечениями могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

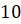
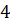
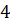
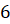
Задача первая. В основании прямой призмы лежит равнобедренная трапеция с основаниями, равными см и см, и боковой стороной, равной см. Боковое ребро призмы равно см. Найдите площадь сечения призмы плоскостью, проходящей через большую сторону основания и середину противоположного бокового ребра призмы.

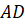
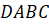
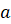
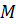
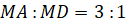
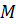
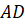
Задача вторая. На ребре правильного тетраэдра с длиной ребра взята точка такая, что . Найдите площадь сечения тетраэдра плоскостью, содержащей точку и перпендикулярной ребру .

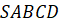
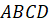
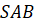
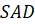
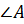
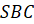
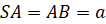
Задача третья. В основании четырёхугольной пирамиды лежит квадрат , а две боковые грани и представляют собой прямоугольные треугольники с прямым . Найдите площадь сечения пирамиды плоскостью, содержащей точку пересечения диагоналей основания и параллельной грани , если .

Источник

Многогранники: призма, параллелепипед, куб

Определение

Многогранником будем называть замкнутую поверхность, составленную из многоугольников и ограничивающую некоторую часть пространства.

Отрезки, являющиеся сторонами этих многоугольников, называются ребрами многогранника, а сами многоугольники – гранями. Вершины многоугольников называются вершинами многогранника.

Будем рассматривать только выпуклые многогранники (это такой многогранник, который находится по одну сторону от каждой плоскости, содержащей его грань).

Многоугольники, из которых составлен многогранник, образуют его поверхность. Часть пространства, которую ограничивает данный многогранник, называется его внутренностью.

Определение: призма

Рассмотрим два равных многоугольника \(A_1A_2A_3. A_n\) и \(B_1B_2B_3. B_n\) , находящихся в параллельных плоскостях так, что отрезки \(A_1B_1, \ A_2B_2, . A_nB_n\) параллельны. Многогранник, образованный многоугольниками \(A_1A_2A_3. A_n\) и \(B_1B_2B_3. B_n\) , а также параллелограммами \(A_1B_1B_2A_2, \ A_2B_2B_3A_3, . \) , называется ( \(n\) -угольной) призмой.

Многоугольники \(A_1A_2A_3. A_n\) и \(B_1B_2B_3. B_n\) называются основаниями призмы, параллелограммы \(A_1B_1B_2A_2, \ A_2B_2B_3A_3, . \) – боковыми гранями, отрезки \(A_1B_1, \ A_2B_2, \ . A_nB_n\) – боковыми ребрами.
Таким образом, боковые ребра призмы параллельны и равны между собой.

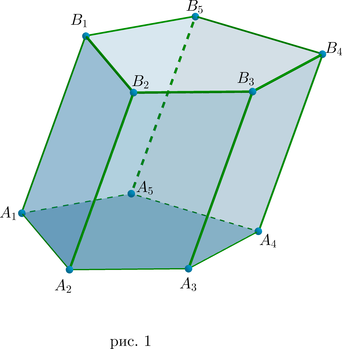
Рассмотрим пример — призма \(A_1A_2A_3A_4A_5B_1B_2B_3B_4B_5\) , в основании которой лежит выпуклый пятиугольник.

Высота призмы – это перпендикуляр, опущенный из любой точки одного основания к плоскости другого основания.

Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (рис. 1), в противном случае – прямой. У прямой призмы боковые ребра являются высотами, а боковые грани – равными прямоугольниками.

Если в основании прямой призмы лежит правильный многоугольник, то призма называется правильной.

Определение: понятие объема

Единица измерения объема – единичный куб (куб размерами \(1\times1\times1\) ед \(^3\) , где ед — некоторая единица измерения).

Можно сказать, что объем многогранника – это величина пространства, которую ограничивает этот многогранник. Иначе: это величина, числовое значение которой показывает, сколько раз единичный куб и его части вмещаются в данный многогранник.

Объем имеет те же свойства, что и площадь:

1. Объемы равных фигур равны.

2. Если многогранник составлен из нескольких непересекающихся многогранников, то его объем равен сумме объемов этих многогранников.

3. Объем – величина неотрицательная.

4. Объем измеряется в см \(^3\) (кубические сантиметры), м \(^3\) (кубические метры) и т.д.

1. Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.
Площадь боковой поверхности — сумма площадей боковых граней призмы.

2. Объем призмы равен произведению площади основания на высоту призмы: \[V_<\text<призмы>>=S_<\text<осн>>\cdot h\]

Определение: параллелепипед

Параллелепипед – это призма, в основании которой лежит параллелограмм.

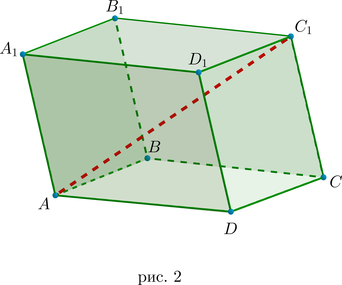
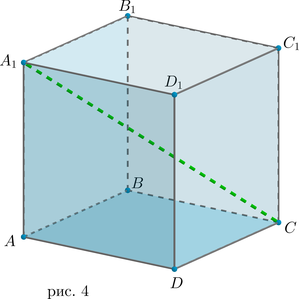
Все грани параллелепипеда (их \(6\) : \(4\) боковые грани и \(2\) основания) представляют собой параллелограммы, причем противоположные грани (параллельные друг другу) представляют собой равные параллелограммы (рис. 2).

Диагональ параллелепипеда – это отрезок, соединяющий две вершины параллелепипеда, не лежащие в одной грани (их \(8\) : \(AC_1, \ A_1C, \ BD_1, \ B_1D\) и т.д.).

Прямоугольный параллелепипед — это прямой параллелепипед, в основании которого лежит прямоугольник.
Т.к. это прямой параллелепипед, то боковые грани представляют собой прямоугольники. Значит, вообще все грани прямоугольного параллелепипеда – прямоугольники.

Все диагонали прямоугольного параллелепипеда равны (это следует из равенства треугольников \(\triangle ACC_1=\triangle AA_1C=\triangle BDD_1=\triangle BB_1D\) и т.д.).

Таким образом, параллелепипед обладает всеми свойствами призмы.

Площадь боковой поверхности прямоугольного параллелепипеда равна \[S_<\text<боков.пов-ти прямоуг. пар-да>>=2(a+b)c\]

Площадь полной поверхности прямоугольного параллелепипеда равна \[S_<\text<полн.пов-ти прямоуг. пар-да>>=2(ab+ac+bc)\]

Объем прямоугольного параллелепипеда равен произведению трех его ребер, выходящих из одной вершины (три измерения прямоугольного параллелепипеда): \[V_<\text<прямоуг.пар-да>>=abc\]

Доказательство

Т.к. у прямоугольного параллелепипеда боковые ребра перпендикулярны основанию, то они являются и его высотами, то есть \(h=AA_1=c\) Т.к. в основании лежит прямоугольник, то \(S_<\text<осн>>=AB\cdot AD=ab\) . Отсюда и следует данная формула.

Диагональ \(d\) прямоугольного параллелепипеда ищется по формуле (где \(a,b,c\) — измерения параллелепипеда) \[d^2=a^2+b^2+c^2\]

Доказательство

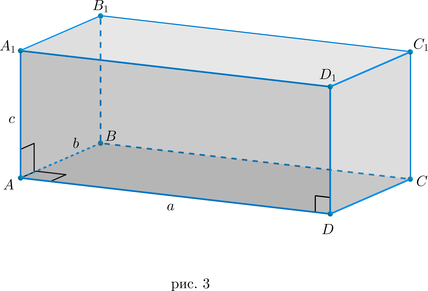
Рассмотрим рис. 3. Т.к. в основании лежит прямоугольник, то \(\triangle ABD\) – прямоугольный, следовательно, по теореме Пифагора \(BD^2=AB^2+AD^2=a^2+b^2\) .

Т.к. все боковые ребра перпендикулярны основаниям, то \(BB_1\perp (ABC) \Rightarrow BB_1\) перпендикулярно любой прямой в этой плоскости, т.е. \(BB_1\perp BD\) . Значит, \(\triangle BB_1D\) – прямоугольный. Тогда по теореме Пифагора \(B_1D=BB_1^2+BD^2=a^2+b^2+c^2\) , чтд.

Определение: куб

Куб — это прямоугольный параллелепипед, все грани которого – равные квадраты.

Таким образом, три измерения равны между собой: \(a=b=c\) . Значит, верны следующие

1. Объем куба с ребром \(a\) равен \(V_<\text<куба>>=a^3\) .

2. Диагональ куба ищется по формуле \(d=a\sqrt3\) .

3. Площадь полной поверхности куба \(S_<\text<полн.пов-ти куба>>=6a^2\) .

Источник