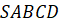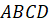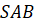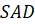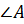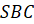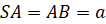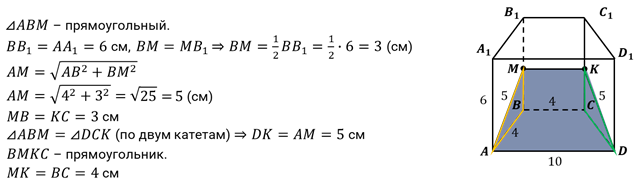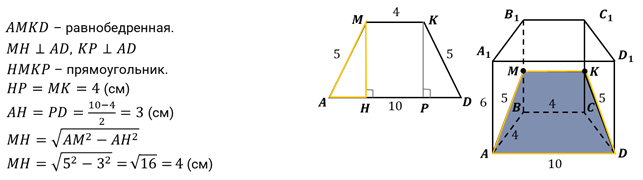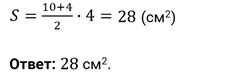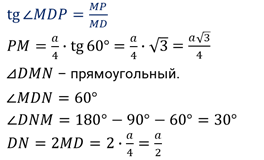Пирамида врезана в куб

Посмотрите, пожалуйста, правильная врезка в куб?

1) Не очень удачный ракурс, в котором вы запутались. Для начала стоило разобраться с построением в ортогональных проекциях.

2) Погрешности в построении за ошибку считать не будем, иначе придётся всё нафиг стирать.

3) На нижней грани куба (его основании) я бы обозначил проекцию основания пирамиды, чтобы показать, насколько пирамида сдвинута относительно куба в горизонтальной плоскости. Сопоставление с этой проекцией сразу дало бы вам верное представление о том, как надо строить пересечение фигур.

4) Чтобы понять ту ошибку, которую вы допустили, проще всего построить эту же ситуацию в Google SketchUp и повертеть с разных сторон. Вы сразу увидите свой косяк.

5) Левое нижнее ребро пирамиды, судя по рисунку, идёт параллельно с плоскостью находящейся рядом грани куба. Но тогда, если пирамида вышла за грань куба, то её нижнее левое ребро будет видно полностью, а у вас оно прерывается, как будто вошло в куб. В куб вошло правое ребро, да. А вот левое с кубом пересекаться не должно. Ведь пирамида должна загораживать куб, а не наоборот. Линия пересечения нижней грани (основания) пирамиды с кубом тоже будет непрерывной (ведите её дальше влево). И к тому же эта линия совершенно напрасно привязана вами к проекции вершины пирамиды на её основание. Это в данном случае грубая ошибка, ведь пирамида совершенно очевидно не наполовину выступает из куба, а меньше.

6) Чтобы правильно построить наклонные линии пересечения поверхностей, вообще-то нужно вписать пирамиду в параллелепипед, на сторонах которого обозначить ортогональные проекции пирамиды — и с помощью такой вспомогательной конструкции уже искать линии пересечения. По сути нужно спроецировать точки пересечения куба и пирамиды с ортогональной проекции в соответствующие точки пространства, и только потом проводить линии.

7) Если пирамида всё-таки развёрнута под углом по отношению к кубу, то линия пересечения основания пирамиды с кубом (там где пирамида выступает из куба) должна тем более быть прямой. Она не будет делать никаких зигзагов, как у вас сейчас. И потом, в таком случае нужно более явно обозначить, насколько пирамида развёрнута вокруг своей вертикальной оси.

Короче, добрая половина проблем решилась бы, если бы вы умели строить положения точек в пространстве по их ортогональным проекциям (как минимум нам нужна проекция фигур на основание, где они стоят). Но вы пытались строить всё по отдельности, пытались сразу чертить врезку в пространстве — и очень сильно запутались.

Источник

Врезка шара и куба по заданным ортогональным проекциям

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку куба и шара.

ПОСТАНОВКА ЗАДАНИЯ. Нарисуйте связки куба и шара по заданным ортогональным проекциям.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ. Рассмотрите ортогональные проекции на рис. 5.70. Центр шара совпадает с вершиной куба. Изобразите эту связку в двух вариантах – с верхней и нижней линией горизонта.

Для первого рисунка выберите верхнюю точку зрения, когда линия горизонта проходит выше геометрических тел. Изобразите куб в перспективе, начав построение, как обычно, с горизонтального квадрата, описанного вокруг эллипса. Затем определите, какая вершина куба станет центром шара, и наметьте окружность (абрис шара) с центром в этой точке (рис. 5.71). Диаметр абриса шара будет несколько меньше большой оси эллипса, вписанного в квадрат основания куба, так как центр шара находится дальше от зрителя, чем центр окружности в верхнем основании куба.

Шар рассекается по центру гранями куба – тремя взаимно перпендикулярными плоскостями. Построение таких сечений вам хорошо знакомо. Начните построение, как обычно, с горизонтального эллипса.

Он должен пройти через середины сторон верхнего основания куба. Учитывая это, уточите диаметр шара и его абрис, а затем постойте два вертикальных сечения (рис. 5.72). Проанализируйте полученную линию врезки – на рис. 5.73 она выделена графически.

Линия врезки замкнута и состоит из сегментов трех различных эллипсов. Точки, в которых один эллипс сменяет другой, лежат на ребрах куба. Тонируйте полученную связку, выявляя ее объем (рис. 5.74).

Изобразите эту же связку шара и куба с нижней линией горизонта (рис. 5.75 и 5.76).

Источник

Врезка куба и пирамиды

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку куба и пирамиды. Оценить многообразие возможных связок куба и пирамиды, отработать приемы построения их врезок, научиться создавать на листе связки с гармоничными пропорциями.

ПОСТАНОВКА ЗАДАНИЯ. Нарисуйте связки куба и пирамиды сначала по заданным ортогональным проекциям, а затем в произвольном положении по отношению друг к другу. Найдите наиболее красивые, гармоничные пропорции связок, изменяя положение линии пересечения геометрических тел.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ

Рассмотрите ортогональные проекции двух геометрических тел – куба и пирамиды – на рис. 5.20. Представьте взаимное положение тел. Изобразите в перспективе заданную связку куба и пирамиды с различным положением относительно линии горизонта (выше линии горизонта на рис. 5.21 и ниже линии горизонта на рис. 5.22).

Изобразите куб и пирамиду в положении, представленном на рис. 5.23. Предложите несколько вариантов врезок, например, как на рис. 5.24; 5.25 и
5.26.

Теперь попробуйте сделать подобное упражнение, увеличив количество геометрических тел. Связка тел – куба и трех пирамид – предлагается на рис. 5.27. Когда на рисунке взаимодействуют не два, а четыре геометрических тела, сложнее найти гармонию их объемов и линий пересечения. Постройте врезки, например, как это сделано на рис. 5.28. Легко тонируйте композицию (рис. 5.29 и 5.30).

Другой вариант этого задания представлен на рис. 5.31; 5.32 и 5.33.

Источник

Сечения куба, призмы, пирамиды

Урок 37. Подготовка к ЕГЭ по математике

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока «Сечения куба, призмы, пирамиды»

Для решения большинства задач из раздела стереометрии необходимы знания и навыки в построении сечения объёмных тел. Именно об этом мы сейчас с вами и поговорим.

Итак, секущей плоскостью называют любую плоскость, по обе стороны от которой имеются точки данной фигуры.

Секущая плоскость пересекает грани многогранника по отрезкам.

Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Построить сечение многогранника плоскостью – это значит указать точки пересечения секущей плоскости с рёбрами многогранника и соединить эти точки отрезками, принадлежащими граням многогранника.

Теперь давайте вспомним, что нам необходимо знать для построения плоскости.

Итак, построить плоскость можно: с помощью трёх точек, не лежащих на одной прямой;

с помощью двух пересекающихся прямых;

с помощью прямой и точки, которая не лежит на прямой;

а также с помощью двух параллельных прямых.

Метод следов включает три важных пункта: сначала нужно построить линию пересечения (след) секущей плоскости с плоскостью основания многогранника; затем найти точки пересечения секущей плоскости с рёбрами многогранника, а после этого построить и заштриховать сечение.

В основе построения сечения методом следов лежат две теоремы:

1) если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости;

2) если плоскость проходит через прямую, параллельную другой плоскости, и эти плоскости пересекаются, то линия их пересечения параллельна первой прямой.

Метод вспомогательных сечений применяется при построении сечений в тех случаях, когда неудобно находить след секущей плоскости. Например, след получается очень далеко от заданной фигуры.

Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с методом следов или методом вспомогательных сечений.

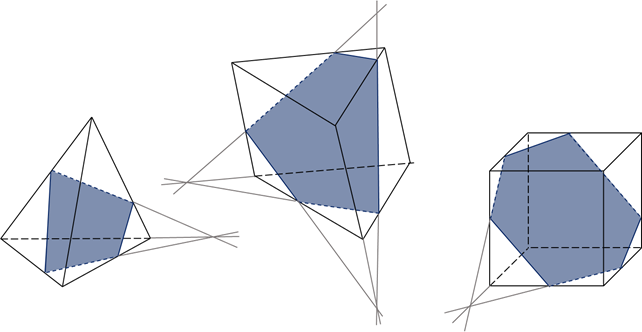
Обратите внимание: тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырёхугольники. А вот параллелепипед имеет шесть граней, поэтому его сечениями могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

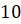
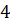
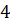
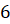
Задача первая. В основании прямой призмы лежит равнобедренная трапеция с основаниями, равными см и см, и боковой стороной, равной см. Боковое ребро призмы равно см. Найдите площадь сечения призмы плоскостью, проходящей через большую сторону основания и середину противоположного бокового ребра призмы.

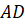
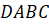
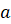
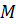
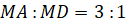
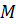
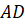
Задача вторая. На ребре правильного тетраэдра с длиной ребра взята точка такая, что . Найдите площадь сечения тетраэдра плоскостью, содержащей точку и перпендикулярной ребру .

Задача третья. В основании четырёхугольной пирамиды лежит квадрат , а две боковые грани и представляют собой прямоугольные треугольники с прямым . Найдите площадь сечения пирамиды плоскостью, содержащей точку пересечения диагоналей основания и параллельной грани , если .

Источник