Перечислите прямые параллельные ad bb1 bd куб 1 вариант

Самостоятельная работа на тему «Параллельность прямых в пространстве и параллельность прямой и плоскости»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Сформулируйте определение параллельных прямых в пространстве. Сформулируйте признак параллельности прямой и плоскости Сформулируйте определение параллельности прямой и плоскости. Сформулируйте признак параллельности прямых в пространстве.

1 вариант 2 вариант А В С D D1 С1 В1 А1 куб А В С D А1 В1 С1 D1 параллелепипед 3. Перечислите прямые, параллельные а) AD б) BB1 в) BD 4. Укажите плоскости, параллельные прямой а) AB б) DD1 в) B1C 3. Перечислите прямые, параллельные а) AB б) CC1 в) AD1 4. Укажите плоскости, параллельные прямой а) BC б) BB1 в) BD

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 595 604 материала в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

1.1. Параллельные прямые в пространстве

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Добавить в избранное

• 19.11.2017 6664
• PPTX 143 кбайт
• 67 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Кизилова Елена Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

В Швеции запретят использовать мобильные телефоны на уроках

В приграничных пунктах Брянской области на день приостановили занятия в школах

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Академическая стипендия для вузов в 2023 году вырастет до 1 825 рублей

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Перечислите прямые параллельные ad bb1 bd куб 1 вариант

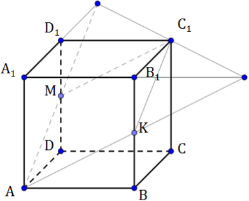
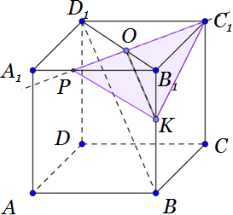
В кубе ABCDA₁B₁C₁D₁ все рёбра равны 7. На его ребре BB₁ отмечена точка K так. что KB = 4. Через точки K и C₁ проведена плоскость α, параллельная прямой BD₁.

б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

а) Проведём через точку K прямую, параллельную BD₁. Пусть эта прямая пересекает плоскость грани A₁B₁C₁D₁ в точке L. Прямая KL лежит в плоскости BB₁D₁, значит, точка L лежит на диагонали B₁D₁. Более того,

Прямая C₁L пересекает ребро A₁B₁ в точке P, принадлежащей плоскости α.

Значит,

б) Объём куба ABCDA₁B₁C₁D₁ равен 343. Объём тетраэдра PKC₁B₁ равен одной шестой произведения его измерений:

Значит, объём оставшейся части равен

Ответ: б)

Источник

Перечислите прямые параллельные ad bb1 bd куб 1 вариант

Задание 14. В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре ВВ1 отмечена точка K так, что KB=3. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.

а) Докажите, что A1P:PB1 =2:1, где Р — точка пересечения плоскости α с ребром А1В1.

б) Найдите угол наклона плоскости α к плоскости грани ВВ1С1C.

а) Проведём через точку K прямую, параллельную BD1. Пусть эта прямая пересекает плоскость грани A1B1C1D1 в точке L. Прямая KL лежит в плоскости BB1D1, значит, точка L лежит на диагонали B1D1. Более того, B1L:LD1 =В1K:KB=1:3.

Прямая C1L пересекает ребро А1В1 в точке Р, принадлежащей плоскости α. Треугольники B1LP и D1LC1 подобны, поэтому B1P:D1C1=B1L:D1L=1:3. Значит, A1Р:РВ1 =2:1.

б) Опустим из точки перпендикуляр В1Н на C1K. По теореме о трёх перпендикулярах прямые РН и C1K перпендикулярны. Значит, угол B1HP искомый.

Поскольку А1Р:РВ1 = 2:1, получаем PB1 = 4/3. В прямоугольном треугольнике B1C1K:

.

.

Ответ: .

Источник

14. Стереометрия

Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.

Примеры ответов: 7 или здесьисейчас или 3514

Найдите площадь сечения, вершинами которого являются вершина А и середины рёбер ВВ₁ и DD₁единичного куба АВСDA₁B₁C₁D₁.

Дополнительное построение К – середина ребра ВВ₁ и М – середина ребра DD₁.

Строим сечение методом следов:

• Соединяем вершины, лежащие в одной грани, А и К, А и М.
• Продлеваем прямые АК и А₁В₁ до пересечения. Также прямые АМ и A₁D₁.
• Соединяем точки и видим, что прямая, проходит через точку С₁, которая принадлежит нашему сечению.
• Соединяем оставшиеся точки.

Сечением является ромб. Найдем его сторону по теореме Пифагора:

Большая диагональ куба является диагональю куба – АС₁.

Найдем угол АКС₁ по теореме косинусов:

$AC_1^2=AK^2+KC_1^2-2\cdot AK\cdot KC_1\cdot\cos AKC_1 \\[5pt] 3=\displaystyle\frac<5><4>+\frac<5><4>-2\cdot\frac<5><4>\cdot\cos AKC_1 \\[2pt] \cos AKC_1=-\displaystyle\frac<1><5>$

Найдем площадь искомого сечения:

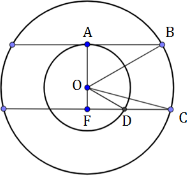
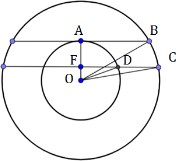
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5. Найдите площадь сечения большего шара плоскостью α.

Сечение шара плоскостью – круг.

Дополнительное построение – плоскость α имеет радиус АВ, плоскость β – FD и FC.

Площадь сечения большего шара плоскостью, параллельной первоначальной плоскости, равна 5. Значит: $S=\pi R^2=\pi\cdot AB^2=5$

Аналогичным образом найдем $FD^2=\displaystyle\frac<7><\pi>$

Для того, чтобы найти площадь искомого сечения, надо знать, чему равно CF 2 .

Применим теорему Пифагора:

Вычтем из одного уравнения другое.

Применим еще раз теорему Пифагора:

$OA^2+AB^2-OD^2=FC^2-FD^2 \\[3pt] OD=OA\rightarrow AB^2=FC^2-FD^2 \\ FC^2=AB^2+FD^2=\displaystyle\frac<5><\pi>+\frac<7><\pi>=\frac<12><\pi>$

Также возможен случай, когда плоскости будут по одну сторону от центра. Решение будет аналогичным.

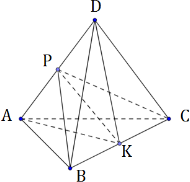
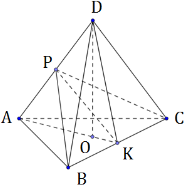
В треугольной пирамиде ABCD двугранные углы при рёбрах AD и BC равны. AB = BD = CD = AC = 5.

б) Найдите объем пирамиды, если двугранные углы при AD и BC равны 60.

1) Дополнительное построение:

2) Треугольники АВС и АBD равнобедренные по условию, значит, АК и BP будут являться медианами по свойству равнобедренного треугольника. Тогда DK, СР также являются одновременно медианой и высотой.

Тогда ∠BPC – линейный угол двугранного угла при ребре AD, ∠AKD — линейный угол двугранного угла при ребре ВС. Из условия имеем: ∠BPC = ∠AKD.

3) РК медиана, биссектриса и высота в треугольниках ВРС и AKD. Тогда PK ⊥ BC и PK ⊥ AD.

Тогда, треугольник BPK равен треугольнику АКР по углу

$\angle BPK=\displaystyle\frac<1><2>\angle BPC=\frac<1><2>\angle AKD=\angle AKP$ и катету РК.

Из равенства треугольников следует, что BK = AP.

$BK=\displaystyle\frac<1><2>BC \\[3pt] AP=\displaystyle\frac<1><2>AD$

1) По данным пункта б: ∠BPC = ∠AKD = 60°, тогда треугольники АКD и ВРС равносторонние. Пусть сторона каждого такого треугольника будет равна х.

2) Дополнительное построение. Пусть DO⊥ AK.

$\left\<\beginBC\perp KD\ (&по\ доказанному\ в\ пункте\ а) \\ BC\perp AK\ (&по\ доказанному\ в\ пункте\ а) \\ &KD\cap AK=K\end\right.\!\!\!\Rightarrow BC\perp AKD\ <(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)>$

Из доказанного следует, что BC ⊥ OD. Значит:

То есть, OD – высота пирамиды.

3) AK = x по построению, тогда $BK=\displaystyle\frac<2>.\ AB=5$.

Треугольник АВК прямоугольный, значит:

4) Высота пирамиды и равностороннего треугольника равна:

5) Площадь основания равна:

$S_=\displaystyle\frac<1><2>AK\cdot BC=\frac<1><2>\cdot x\cdot x=\frac<1><2>\cdot 2\sqrt<5>\cdot 2\sqrt<5>=10 \\ V=\displaystyle\frac<1><3>\cdot h\cdot S_=\frac<1><3>\cdot\sqrt<15>\cdot 10=\frac<10\sqrt<15>><3>$

В кубе $ABCDA_1B_1C_1D_1$ все рёбра равны 5. На его ребре BB₁ отмечена
точка K так, что KB = 3. Через точки K и С₁ проведена плоскость α, параллельная прямой BD₁.

а) Докажите, что $\displaystyle\frac=\frac<1><2>$, где P — точка пересечения плоскости α с ребром A₁B₁.

б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

а) 1. Дополнительное построение.

Пусть B₁D₁ пересекается с построенной прямой в точке О.

Прямая BD₁параллельная плоскости С₁ОК, так как параллельна как минимум одной прямой ОК (по построению), лежащей в этой плоскости.

2) Через точку С₁ и О проведем прямую. Пусть прямая С₁О пересекается с A₁B₁в точке Р. Точка Р – точка пересечения плоскости α с ребром A₁B₁.

3) В треугольнике BB₁D отрезок ОК параллелен BD₁. Значит отрезок ОК делит треугольник BB₁D на 2 подобных (признак подобия по 2 углам).

Что и требовалось доказать.

Ребро РВ₁ перпендикулярно В₁С₁К, так как $ABCDA_1B_1C_1D_1$ — куб, а значит является высотой пирамиды.

Найдем объем другой части куба.

Из объема всего куба вычтем объем пирамиды.

Источник