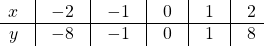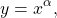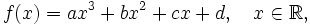Парабола икс в кубе

Кубическая функция

Кубическая функция — это функция вида y=ax³, где a — число ( a≠0).

График кубической функции называется кубической параболой.

Для начала рассмотрим свойства и график кубической функции y=x³ (при a=1).

Свойства функция y=x³:

1) Область определения — множество действительных чисел:

2) Область значений — все действительные числа:

3) Функция имеет один нуль:

4) Точка O (0;0) делит кубическую параболу на две равные части, каждая из которых называется ветвью кубической параболы. Ветви кубической параболы симметричны относительно точки O — начала координат.

Отсюда следует, что противоположным значениям x соответствуют противоположные значения y: (- x)³= — x³ .

5) Функция возрастает на всей числовой прямой.

6) Промежутки знакопостоянства: функция принимает положительные значения при x∈(0;∞) (или y>0 при x>0);

функция принимает отрицательные значения при x∈(-∞;0) (или y

Эти точки отмечаем на координатной плоскости и строим кубическую параболу:

График функции y=ax³ при a≠1 ( a≠0) получают из графика функции y=x³ при помощи геометрических преобразований.

Функция y=x³ — один из частных случаев степенной функции

где α — любое действительное число.

В курсе алгебры из частных случаев степенной функции мы уже встречались с квадратичной функцией y=x² и функцией обратной пропорциональности

Источник

Кубическая парабола

Вы будете перенаправлены на Автор24

Кубическая парабола – это парабола, задаваемая уравнением вида $y=ax^3$, где $a ≠ 0$. Также в литературе можно встретить и другие формулы для кубической параболы, все они эквивалентны.

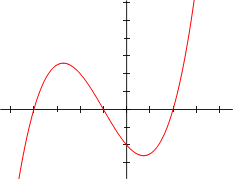
Рисунок 1. График кубической параболы

Свойства функции кубической параболы

1. График кубической параболы определён на всём пространстве действительных чисел.
2. Функция, задаваемая графиком кубической параболы, является нечётной, то есть: $f(-x) =(-x)^3= — x^3 = f(x)$.
3. Из этого следует, что обратная функция кубической параболы, заданная уравнением $y = -x^3$ будет располагаться II и IV четвертях графика, тогда как для $y = x^3$ график располагается в I и III четвертях.
4. График кубической параболы центрально-симметричен относительно начала координат или точки перегиба, если он сдвинут относительно начала координат. То есть форма кривой справа до точки перегиба полностью идентична форме кривой слева. График кубической параболы хотя бы 1 раз пересекает ось абсцисс.
5. График кубической параболы возрастает на всей области определения.

Анализ графика функции кубической параболы

1. Найдя производную $f'(x)$ кубической функции первого порядка и приравняв полученное выражение к нулю, вы получите критические точки для кубической параболы, называемые также локальными минимумами и максимумами.
2. Вторая производная $f»(x)$ параболы определяет точку перегиба функции.
3. Области значения и определения кубической параболы — все действительные числа.

Найдите точку перегиба для кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$.

1. Сначала найдём первую производную функции, она равна: $y’ = 6x^2 + 12x – 1$.
2. Теперь найдём вторую производную, $y» = 12x + 12$. Чтобы найти значение по оси абсцисс точки перегиба, приравняем вторую производную к нулю и решим уравнение: $12x + 12 = 0$, $x = -1$.
3. Найдём значение по оси ординат, для этого в исходную функцию подставим значение найденного $x$: $y = -2 + 6 + 1 +2 = 7$. Точка перегиба кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$ находится по координатам $(-1; 7)$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 09 12 2021

Источник

Кубическая парабола

Куби́ческая фу́нкция в математике — это числовая функция 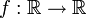вида

где 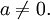Другими словами кубическая функция задаётся многочленом третьей степени.

Содержание

Аналитические свойства

Производная кубической функции f(x) = ax 3 + bx 2 + cx + d имеет вид f‘(x) = 3ax 2 + 2bx + c . В случае, когда дискриминант D = b 2 − 4ac квадратного уравнения f‘(x) = 0 больше нуля, оно имеет два различных решения, которые соответствуют критическим точкам функции f . При этом, одна из этих точек является точкой локального минимума, а другая точкой локального максимума. Равенство нулю второй производной f» определяет точку перегиба x = − b / 3a .

График

График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции y = ax 3 или y = x 3 . Легко видеть, что применяя параллельный перенос можно привести кубическую параболу к виду, когда она будет задаватся уравнением y = ax 3 − px . Путём применения аффинных преобразований плоскости можно добиться, чтобы a = 1 и p = 0 . В этом смысле все определения будут эквивалентны.

Кроме того, кубическая парабола

• центрально-симметрична относительно точки перегиба,
• всегда пересекает линию абсцисс хотя бы в одной точке,
• не имеет общих точек со своей касательной в точке перегиба, кроме как в самой точке касания.

См. также

Литература

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Кубическая парабола» в других словарях:

КУБИЧЕСКАЯ ПАРАБОЛА — алгебраическая кривая 3 го порядка: y = x3 … Большой Энциклопедический словарь

кубическая парабола — алгебраическая кривая 3 го порядка: у = х3. * * * КУБИЧЕСКАЯ ПАРАБОЛА КУБИЧЕСКАЯ ПАРАБОЛА, алгебраическая кривая 3 го порядка: y = x3 … Энциклопедический словарь

КУБИЧЕСКАЯ ПАРАБОЛА — алгебр кривая 3 го порядка (рис.): у = х3 … Естествознание. Энциклопедический словарь

Кубическая парабола — плоская кривая; см. Линия … Большая советская энциклопедия

КУБИЧЕСКАЯ ПАРАБОЛА — плоская кривая (см, рис.), выражаемая в прямоугольной системе координат уравнением у=ах 3 … Математическая энциклопедия

Парабола кубическая — График кубической функции (кубическая парабола) Кубическая функция в математике это числовая функция вида где Другими словами кубическая функция задаётся многочленом третьей степени … Википедия

Кубическая функция — График кубической функции (кубическая парабола) Кубическая функция в математике это числовая функция … Википедия

Парабола — У этого термина существуют и другие значения, см. Парабола (значения). Парабола, её фокус и директриса Коническое сечение … Википедия

Парабола (значения) — Парабола: Парабола геометрическое место точек, равноудалённых от данной прямой и данной точки. Кубическая парабола числовая функция, задаваемая многочленом третьей степени. Полукубическая парабола (парабола Нейла) плоская алгебраическая кривая.… … Википедия

Кубическая кривая Безье — Кривые Безье были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов… … Википедия

Источник

Парабола кубическая

Куби́ческая фу́нкция в математике — это числовая функция 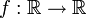вида

где 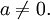Другими словами кубическая функция задаётся многочленом третьей степени.

Содержание

Аналитические свойства

Производная кубической функции f(x) = ax 3 + bx 2 + cx + d имеет вид f‘(x) = 3ax 2 + 2bx + c . В случае, когда дискриминант D = b 2 − 4ac квадратного уравнения f‘(x) = 0 больше нуля, оно имеет два различных решения, которые соответствуют критическим точкам функции f . При этом, одна из этих точек является точкой локального минимума, а другая точкой локального максимума. Равенство нулю второй производной f» определяет точку перегиба x = − b / 3a .

График

График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции y = ax 3 или y = x 3 . Легко видеть, что применяя параллельный перенос можно привести кубическую параболу к виду, когда она будет задаватся уравнением y = ax 3 − px . Путём применения аффинных преобразований плоскости можно добиться, чтобы a = 1 и p = 0 . В этом смысле все определения будут эквивалентны.

Кроме того, кубическая парабола

• центрально-симметрична относительно точки перегиба,
• всегда пересекает линию абсцисс хотя бы в одной точке,
• не имеет общих точек со своей касательной в точке перегиба, кроме как в самой точке касания.

См. также

Литература

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Парабола кубическая» в других словарях:

Парабола кубическая — плоская Линия … Большая советская энциклопедия

кубическая парабола — алгебраическая кривая 3 го порядка: у = х3. * * * КУБИЧЕСКАЯ ПАРАБОЛА КУБИЧЕСКАЯ ПАРАБОЛА, алгебраическая кривая 3 го порядка: y = x3 … Энциклопедический словарь

КУБИЧЕСКАЯ ПАРАБОЛА — алгебраическая кривая 3 го порядка: y = x3 … Большой Энциклопедический словарь

Кубическая парабола — График кубической функции (кубическая парабола) Кубическая функция в математике это числовая функция вида где Другими словами кубическая функция задаётся многочленом третьей степени … Википедия

Кубическая функция — График кубической функции (кубическая парабола) Кубическая функция в математике это числовая функция … Википедия

Кубическая кривая Безье — Кривые Безье были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов… … Википедия

Парабола — У этого термина существуют и другие значения, см. Парабола (значения). Парабола, её фокус и директриса Коническое сечение … Википедия

Парабола (значения) — Парабола: Парабола геометрическое место точек, равноудалённых от данной прямой и данной точки. Кубическая парабола числовая функция, задаваемая многочленом третьей степени. Полукубическая парабола (парабола Нейла) плоская алгебраическая кривая.… … Википедия

КУБИЧЕСКАЯ ПАРАБОЛА — алгебр кривая 3 го порядка (рис.): у = х3 … Естествознание. Энциклопедический словарь

Кубическая парабола — плоская кривая; см. Линия … Большая советская энциклопедия

Источник

Как определить a, b и c по графику параболы

Предположим, вам попался график функции \(y=ax^2+bx+c\) и нужно по этому графику определить коэффициенты \(a\), \(b\) и \(c\). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью \(y\) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент \(a\) можно найти с помощью следующих фактов:

— Если \(a>0\), то ветви параболы направленных вверх, если \(a 1\), то график вытянут вверх в \(a\) раз по сравнению с «базовым» графиком (у которого \(a=1\)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: \(y=ax^2+bx+c\). Получится система с тремя уравнениями.

Вычтем из второго уравнения первое:

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки \(A\) и \(B\) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение \(a\):

Получается квадратичная функция: \(y=-x^2-9x-15\).

Сразу заметим, что по графику можно сразу определить, что \(c=4\). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: \(C(-1;8)\), \(D(1;2)\) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График \(y=-x^2\) симметричен относительно оси \(x\) графику \(y=x^2\).

– Если \(a>1\) график \(y=ax^2\) получается растяжением графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.
– Если \(a∈(0;1)\) график \(y=ax^2\) получается сжатием графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.

– График \(y=a(x+d)^2\) получается сдвигом графика \(y=ax^2\) влево на \(d\) единиц.
— График \(y=a(x-d)^2\) получается сдвигом графика \(y=ax^2\) вправо на \(d\) единиц.

График \(y=a(x+d)^2+e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вверх.
График \(y=a(x+d)^2-e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому \(a=1\). То есть она получена перемещениями графика базовой параболы \(y=x^2\).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на \(4\).

То есть наша функция выглядит так: \(y=(x-5)^2-4\).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти \(f(6)\), надо сначала узнать формулу функции \(f(x)\). Найдем её:

Парабола растянута на \(2\) и ветви направлены вниз, поэтому \(a=-2\). Иными словами, первоначальной, перемещаемой функцией является функция \(y=-2x^2\).

Парабола смещена на 2 клеточки вправо, поэтому \(y=-2(x-2)^2\).

Парабола поднята на 4 клеточки вверх, поэтому \(y=-2(x-2)^2+4\).

Источник