Найти объем куба задачи с ответами

Нахождение объема куба: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.

Формула вычисления объема куба

1. Через длину ребра

Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.

V = a ⋅ a ⋅ a = a 3

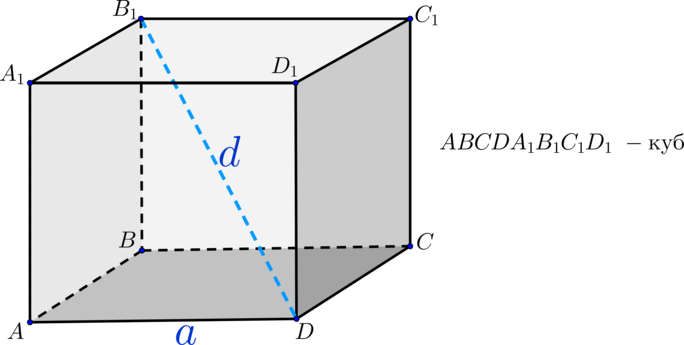
2. Через длину диагонали грани

Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√ 2 .

Следовательно, вычислить объем куба можно так:

Примеры задач

Задание 1
Вычислите объем куба, если его ребро равняется 5 см.

Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .

Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.

Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:

Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.

Решение:
Применим формулу, в которой используется диагональ грани:

Источник

Найти объем куба задачи с ответами

Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Крест состоит из 7 одинаковых кубов, поэтому его объем в 7 раз больше объема одного куба, который равен 1.

Аквариум имеет форму куба со стороной 40 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.

Объем аквариума равен: см 3 или литров.

Шар, объём которого равен 6π, вписан в куб. Найдите объём куба.

Ребро куба равно двум радиусам вписанного в куб шара, поэтому объем куба, выраженный через радиус вписанного в него шара, даётся формулой Объём шара вычисляется по формуле откуда имеем:

Тем самым, объём куба равен 36.

Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 2. Найдите объём куба.

Высота отсчённой призмы равна ребру куба, поэтому их объёмы относятся как площади оснований. Отрезок FE — средняя линия треугольника DBC, поэтому треугольники FCE и DCB подобны с коэффициентом подобия 1 : 2, а их площади относятся как 1 : 4. Поскольку квадрата АDCB вдвое больше площади треугольника DCB, площадь АDCB в 8 раз больше площади треугольника FCE.

Тем самым, объём куба в 8 раз больше объёема отсечённой призмы, поэтому он равен 16.

Источник

Задачи по теме «Куб»

Куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.

\(\blacktriangleright\) для объема куба верна следующая формула (где \(a\) – ребро куба): \[<\Large>\] \(\blacktriangleright\) диагональ куба \(<\Large=3a^2>>\)
\(\blacktriangleright\) площадь поверхности куба равна сумме площадей шести одинаковых квадратов, т.е. \(<\Large>=6a^2>>\)

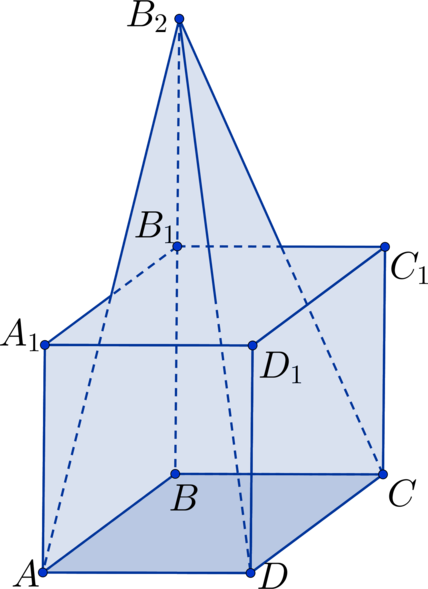
Дан куб \(ABCDA_1B_1C_1D_1\) . Точка \(B_2\) лежит на продолжении ребра \(BB_1\) за точку \(B_1\) , \(BB_2 = 2\cdot BB_1\) . Во сколько раз объем куба отличается от объема пирамиды \(B_2ABCD\) ?

Отрезок \(BB_2\) является высотой пирамиды. Если сторону куба обозначить за \(x\) , то \(BB_2 = 2x\) \(\Rightarrow\) \[\displaystyle V_<\text<пир.>> = \frac<1><3>\cdot BB_2 \cdot S_ = \frac<1><3>\cdot 2x \cdot x^2 = \frac<2><3>\cdot x^3,\,\,\,\, V_<\text<куб>> = x^3.\] Теперь найдем искомую величину: \[\displaystyle \frac>>>> = \frac<\frac<2><3>\cdot x^3> = 1,5.\]

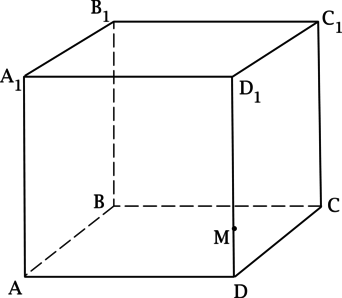
\(ABCDA_1B_1C_1D_1\) – куб с длиной ребра равной \(\sqrt[4]<17>\) . Точка \(M\) лежит на ребре \(DD_1\) так, что \(MD_1 = 3MD\) . Найдите площадь сечения куба, проведённого через точку \(M\) и ребро \(AB\) .

Пусть \(N\) – точка на \(CC_1\) , такая что \(NC_1 = 3NC\) , тогда \(MN\parallel CD\parallel AB\) , следовательно, сечение, проходящее через точку \(M\) и ребро \(AB\) – четырёхугольник \(AMNB\) , причём \((AA_1D_1D) \bot MN\) , следовательно, \(AM \bot MN\) . Аналогично \(MN\bot BN\bot AB\) , то есть \(AMNB\) – прямоугольник. \[S_ = AM\cdot MN = AM\cdot \sqrt[4]<17>.\] Найдём \(AM\) по теореме Пифагора: \[AM = \sqrt = \sqrt = \sqrt<\dfrac<17><16>AD^2> = \dfrac<\sqrt<17>><4>AD = \dfrac<\sqrt[4]<17^3>><4>.\] Тогда \(S_ = \dfrac<\sqrt[4]<17^3>> <4>\cdot \sqrt[4] <17>= \dfrac<17> <4>= 4,25\) .

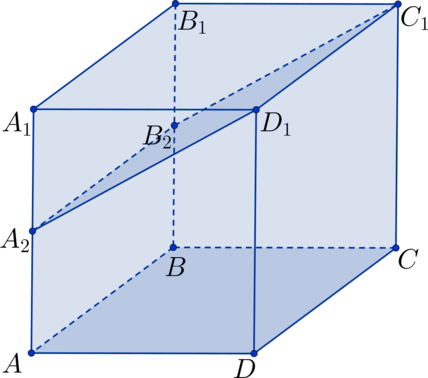
В кубе \(ABCDA_1B_1C_1D_1\) точки \(A_2\) и \(B_2\) – середины соответственно сторон \(AA_1\) и \(BB_1\) . Найдите площадь поверхности фигуры \(ABCDA_2B_2C_1D_1\) , если ребро куба равно \(\sqrt<32 - 4\sqrt5>\) .

Площадь поверхности фигуры \(ABCDA_2B_2C_1D_1\) состоит из суммы следующих площадей: \[S_<\text<пов.>> = S_ + S_ + S_ + S_ + S_ + S_.\] Обозначим ребро куба за \(2x\) , тогда \(AA_2 = BB_2 = x\) . \(AA_2D_1D\) и \(BB_2C_1C\) – равные прямоугольные трапеции, площадь которых равна \[\displaystyle S_ = S_ = \frac<1><2>\cdot(AA_2 + DD_1)\cdot AD = \frac<(x + 2x)\cdot2x> <2>= 3x^2.\] Также найдем площади остальных граней: \(S_ = 4x^2\) , \(S_ = 2x^2\) , \(S_ = 4x^2\) ; для того чтобы найти площадь грани \(A_2B_2C_1D_1\) нам понадобится сначала найти сторону \(A_2D_1\) . Найдем ее, используя теорему Пифагора в треугольнике \(\triangle A_2A_1D_1\) : \[A_2D_1^2 = A_2A_1^2 + A_1D_1^2 = x^2 + 4x^2 = 5x^2\] \(\Rightarrow\) \(A_2D_1 = \sqrt5x\) . Тогда \(S_ = A_2B_2\cdot A_2D_1 = 2\sqrt5x^2\) . Теперь сложим все площади граней искомой фигуры: \[S_<\text<пов.>> = 3x^2 + 3x^2 + 4x^2 + 2x^2 + 4x^2 + 2\sqrt5x^2 = (16 + 2\sqrt5)\cdot x^2.\] По условию задачи имеем: \(2x = \sqrt <32 - 4\sqrt5>= 2\cdot\sqrt<8 - \sqrt5>\) \(\Rightarrow\) \(x = \sqrt<8 - \sqrt5>\) . Подставим в формулу площади и получим окончательный результат: \[S_<\text<пов.>> = (16 + 2\sqrt5)\cdot\left(\sqrt<8 - \sqrt5>\right)^2 = 2\cdot(8 + \sqrt5)\cdot(8 — \sqrt5) = 2\cdot59 = 118.\]

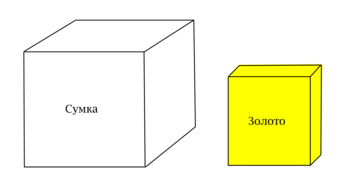
Анатолий грабит банк. Слитки золота имеют форму прямоугольных параллелепипедов с измерениями \(4\times 4\times 2\) . Сумка, которая есть у Анатолия, имеет форму куба с ребром длины \(6\) . Анатолию нужно уложить как можно больше слитков в сумку так, чтобы она закрылась и с ней можно было выйти, не привлекая к ней внимания. Сколько слитков сможет вынести Анатолий, если будет действовать разумно?

Сначала заметим, что ответ не изменится, если уменьшить масштаб в два раза по каждому направлению. При этом сумка станет кубом с ребром \(3\) , а слитки золота станут прямоугольными параллелепипедами с измерениями \(2\times 2\times 1\) .

Оценим возможное количество слитков сверху: так как объём сумки равен \(3^3 = 27\) , а объём слитка равен \(2\cdot 2\cdot 1 = 4\) , то более \(6\) слитков в сумку не войдут. Но могут ли войти в неё 6?

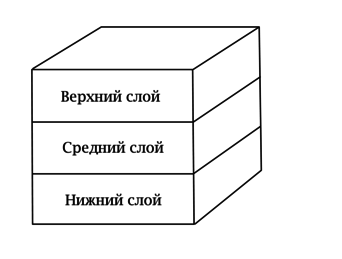
Назовём слиток горизонтальным, если две его грани параллельны дну сумки так, что его высота равна 1. В противном случае назовём слиток вертикальным. Мысленно “расслоим” \(\ \) сумку на 3 одинаковых горизонтальных слоя.

Каждый вертикальный слиток занимает в среднем слое по 2 соседних кубика с ребром 1. Средний слой состоит из 9 таких кубиков, следовательно, вертикальных слитков в сумку входит не более 4. При этом горизонтальных слитков в сумку входит не более 3 (в каждый слой входит не более одного горизонтального слитка).

В случае, когда горизонтальных слитков ровно 3, получим, что в среднем слое 4 кубика из 9 заняты горизонтальным слитком, то есть в среднем слое остаётся \(9 — 4 = 5\) кубиков, но каждый вертикальный слиток должен занимать в среднем слое по 2 кубика, тогда получаем, что вертикальных слитков при этом не более 2 и всего слитков при трёх горизонтальных \(\leq 2 + 3 = 5\) .

Таким образом, последний шанс Анатолия унести 6 слитков – это 4 вертикальных слитка и 2 горизонтальных. Возможно ли это? Понятно, что для этого необходимо, чтобы горизонтальные слитки лежали в нижнем и верхнем слоях, но верхний слиток не должен “полностью нависать” \(\ \) над нижним. Тогда остаётся всего 2 принципиально различных способа уложить горизонтальные слитки в верхнем и нижнем слоях относительно друг друга.

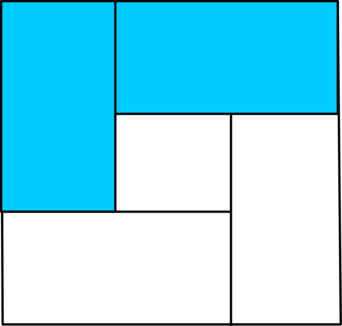
При этом один из них позволяет уложить 6 слитков. Чтобы наглядно проиллюстрировать его сначала поместим в сумку только вертикальные слитки и покажем вид сверху:

здесь голубым отмечены все те вертикальные слитки, которые стоят на дне сумки. Тогда на дно можно подложить ещё 1 горизонтальный слиток под те вертикальные, которые не стоят на дне сумки. Аналогично, в верхний слой можно подложить 1 горизонтальный слиток.

Итого: при разумном подходе Анатолий может вынести 6 слитков.

Источник

Объемы фигур. Объем куба.

Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте).

У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны.

Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна

ширине и равна высоте, то объем куба равен s 3 ,

где s – длина одного (любого) ребра куба.

Воспользуйтесь онлайн калькулятором для расчета объема куба: объем куба, онлайн расчет.

Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.

Метод 1 из 3: Возведение в куб ребра куба

• Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы

вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.

Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.

Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза.

Если s — длина ребра куба, то

и, таким образом, вы вычислите объем куба.

Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на

ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть,

другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и

равна высоте, то это процесс можно заменить возведением ребра куба в третью степень.

В нашем примере объем куба равен:

• К ответу припишите единицы измерения объема. Так как объем – это количественная

характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические

В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических

сантиметрах (или в см 3 ). Итак, объем куба равен 125 см 3 .

Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих

Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м 3 .

Метод 2 из 3: Вычисление объема по площади поверхности

• В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых вы

можете найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите

ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем

возведите длину ребра куба в третью степень и вычислите объем куба.

Площадь поверхности куба равна 6s 2 ,

где s – длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так

как у куба 6 равных граней).

Рассмотрим пример. Площадь поверхности куба равна 50 см 2 . Найдите объем куба.

• Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь

одной грани куба). В свою очередь площадь одной грани куба равна s 2 , где s – длина ребра куба.

В нашем примере: 50/6 = 8,33 см 2 (не забывайте, что площадь измеряется в квадратных единицах — см 2 ,

• Так как площадь одной грани куба равна s 2 , то извлеките квадратный корень из значения площади

одной грани и получите длину ребра куба.

В нашем примере, √8,33 = 2,89 см.

• Возведите в куб полученное значение, чтобы найти объем куба.

В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см 3 . К ответу не забудьте приписать кубические

Метод 3 из 3: Вычисление объема по диагонали

• Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом,

если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив

Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба

равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см 3 .

где d — диагональ грани куба, s – ребро куба. Эта формула вытекает из теоремы Пифагора, согласно

которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен

сумме квадратов катетов (в нашем случае ребер), то есть:

• Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче

дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3.

Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный

(где D — диагональ куба, s – ребро куба).

Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае

диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет –

это ребро, а второй катет – это диагональ грани куба, равная 2s 2 ), то есть

Рассмотрим пример. Диагональ куба равна 10 м. Найдите объем куба.

Источник