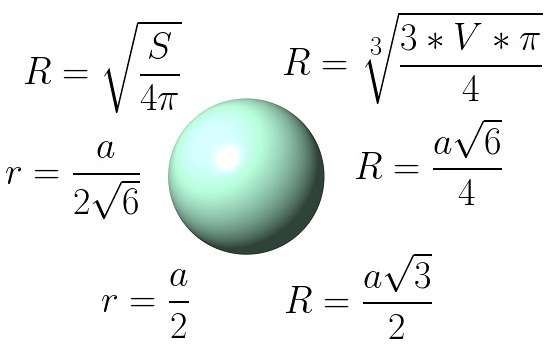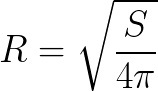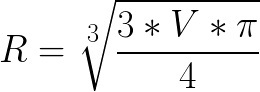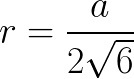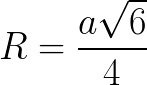Найдите радиус сферы описанной около единичного куба

Как найти радиус сферы

Перед тем, как смело броситься на амбразуру решения задачи по нахождению радиуса сферы, нужно узнать, что вообще такое сфера и шар. Стереометрия говорит нам, что сфера – это поверхность, состоящая из массы точек пространства, которые находятся на одном расстоянии от центра. Эта точка – центр сферы, а радиус сферы (R) – это расстояние, на которое каждая точка удалена от центра сферы. Шар – это тело, которое ограничено поверхностью сферы.

Безусловно, способ определения того самого радиуса сферы будет зависеть от данных, которые у нас есть.

Способ 1. Определение радиуса сферы при помощи площади ее поверхности

Допустим, нам дана сфера вместе с площадью её поверхности. В таком случае мы будем использовать формулу площади её поверхности для того, чтобы вычислить радиус.

где S – это площадь поверхности сферы, число Пи = 3,14.

Способ 2. Определение радиуса сферы при помощи объема шара

Если нам дан объём шара, ограниченного сферой, то радиус находится так:

где V — это объём шара, число Пи = 3,14.

Способ 3. Альтернативные формулы определения радиуса сферы

В случае, если наша сфера вписана в правильный многогранник или описана вокруг него, можно воспользоваться следующим рядом формул.

Формула 1. Сфера вписана в правильный тетраэдр

Для сферы, которая вписана в правильный тетраэдр:

где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).

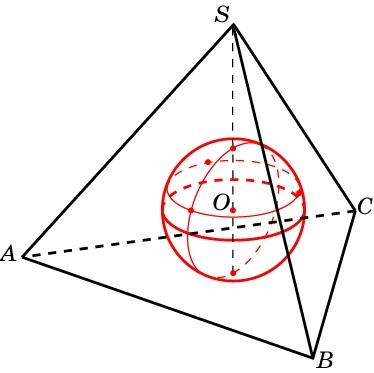
Формула 2. Сфера описана около правильного тетраэдра

Для сферы, которая описана около правильного тетраэдра:

где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).

Источник

Радиус описанной сферы куба

Свойства

Если описать вокруг куба сферу, то ее диаметр будет соединять противоположные вершины куба, образуя диагональ куба. Таким образом, радиус описанной сферы куба равен половине диагонали, следовательно, сама диагональ куба равна удвоенному радиусу описанной сферы. (рис.2.3) D=2R

Так как эта же диагональ связывает теоремой Пифагора в прямоугольном треугольнике диагональ стороны куба и ребро куба, то становится возможным вычислить и их через радиус описанной сферы куба, используя формулы диагонали. D=a√3 a=D/√3=2R/√3 a^2+d^2=D^2 (2R/√3)^2+d^2=(2R)^2 d^2=(8R^2)/3 d=√(8/3) R

Чтобы вычислить площадь грани куба, нужно рассмотреть ее в плоскости. Стороной куба является квадрат, поэтому его площадь равна стороне квадрата, то есть ребру куба, во второй степени. Площадь боковой поверхности куба состоит из четырех боковых граней-квадратов, а площадь полной поверхности – из шести граней, поэтому для их вычисления нужно умножить площадь одной грани на их количество. Чтобы найти площади куба через радиус сферы, описанной вокруг него, нужно подставить вместо ребра куба удвоенный радиус, деленный на корень из трех. S=a^2=(2R/√3)^2=(4R^2)/3 S_(б.п.)=4S=(16R^2)/3 S_(п.п.)=6S=(24R^2)/3

Объем куба, зная радиус описанной вокруг него сферы, вычисляется возведением в третью степень выражения для ребра куба. V=a^3=(2R/√3)^3=(8R^3)/(3√3)

Периметр куба, как умноженное на 12 ребро куба, представлено через радиус описанной вокруг сферы окружности в виде отношения радиуса, умноженного на 24, к корню из трех. P=12a=24R/√3

Чтобы вычислить радиус сферы, вписанной в куб, через радиус сферы, описанной около него, нужно разделить ребро куба на два, то есть разделить радиус описанной сферы на корень из трех. r=a/2=2R/(2√3)=R/√3

Источник

Нахождение радиуса описанной вокруг куба сферы (шара)

В данной публикации мы рассмотрим, чему равняется радиус сферы (шара), описанной около куба, а также как его можно вычислить, если известна длина ребра куба.

Примечание: Напомним, что вокруг любого куба можно описать шар.

Для начала начертим рисунок.

• все 8 вершин куба касаются шара – это их общие точки;
• центр шара – точка O, которая также является точкой пересечения диагоналей куба.

Радиус шара (R), описанного вокруг куба, равняется половине его диагонали, т.е.:

Примечание: все диагонали куба равны.

Чтобы было понятнее, выполним диагональное сечение, т.е. отсечем часть шара вместе со вписанным в него кубом по диагонали куба (линия отреза проходит через точку O).

Таким образом, мы получим прямоугольник с описанной вокруг окружностью, радиус которой равняется половине диагонали прямоугольника.

Примечание: Диагонали прямоугольника равны между собой и одновременно являются диагоналями куба.

Формула расчета радиуса описанного шара через ребро куба

Если известна длина ребра куба (примем ее за “a”), радиус описанного вокруг него шара (R) вычисляется следующим образом:

Источник

Многогранники, вписанные в сферу.

Презентация для учащихся 11 класса по теме «Комбинация тел» содержит краткую теорию и примеры решения задач на комбинации сферы и призмы, сферы и пирамиды. Будет полезна при подготовке к ЕГЭ.

Просмотр содержимого документа
«Многогранники, вписанные в сферу.»

Многогранники, вписанные в сферу

Многогранник называется вписанным в сферу, если все его вершины принадлежат этой сфере. Сама сфера при этом называется описанной около многогранника.

Теорема. Около пирамиды можно описать сферу тогда и только тогда, когда около основания этой пирамиды можно описать окружность.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Многогранники, вписанные в сферу

Теорема. Около призмы можно описать сферу тогда и только тогда, когда около основания этой призмы можно описать окружность. Ее центром будет точка O , являющаяся серединой отрезка, соединяющего центры окружностей, описанных около оснований призмы. Радиус сферы R вычисляется по формуле

где h – высота призмы, r – радиус окружности, описанной около основания призмы.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Можно ли описать сферу около прямоугольного параллелепипеда?

Ответ: Да. Ее центром является точка пересечения диагоналей, а радиус равен половине диагонали параллелепипеда

Можно ли описать сферу около наклонного параллелепипеда, все грани которого ромбы?

Можно ли описать сферу около наклонной призмы?

Может ли центр сферы, описанной около призмы, находится вне призмы?

Ответ: Да, если в основании призмы – тупоугольный треугольник.

Может ли центр сферы, описанной около пирамиды, находится вне этой пирамиды?

Сфера, описанная около куба

В режиме слайдов ответы и решения появляются после кликанья мышкой

Найдите радиус сферы, описанной около единичного куба.

Найдите ребро куба, вписанного в единичную сферу.

Найдите радиус сферы, описанной около прямоугольного параллелепипеда, ребра которого, выходящие из одной вершины, равны 1, 2, 3.

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 2. Радиус описанной сферы равен 1,5 . Найдите третье ребро, выходящее из той же вершины параллелепипеда.

Сфера, описанная около тетраэдра

В режиме слайдов ответы и решения появляются после кликанья мышкой

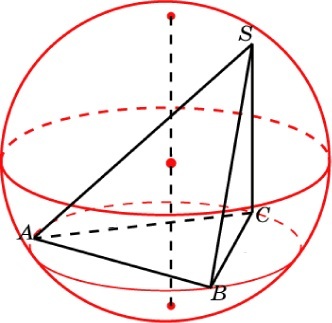
Найдите радиус сферы, описанной около единичного тетраэдра.

Решение. В тетраэдре SABC имеем:

В прямоугольном треугольнике OBE имеем:

Решая это уравнение относительно R , находим

Найдите ребро правильного тетраэдра, вписанного в единичную сферу.

Основанием пирамиды служит правильный треугольник, сторона которого равна 3. Одно из боковых ребер равно 2 и перпендикулярно плоскости основания. Найдите радиус описанной сферы.

Решение. Пусть O – центр описанной сферы, Q – центр окружности, описанной около основания, E – середина SC . Четырехугольник CEOQ – прямоугольник, в котором CE = 1, CQ = Следовательно, R=OC= 2.

На рисунке изображена пирамида SABC , для которой ребро SC равно 2 и перпендикулярно плоскости основания ABC , угол ACB равен 90 о , AC = BC = 1 . Постройте центр сферы, описанной около этой пирамиды и найдите ее радиус.

Решение. Через середину D ребра AB проведем прямую, параллельную SC . Через середину E ребра SC проведем прямую параллельную CD . Их точка пересечения O будет искомым центром описанной сферы. В прямоугольном треугольнике OCD имеем:

Найдите радиус сферы, описанной около правильной треугольной пирамиды, боковые ребра которой равны 1, и плоские углы при вершине равны 90 о .

Решение. В тетраэдре SABC имеем:

В прямоугольном треугольнике OAE имеем:

Решая это уравнение относительно R , находим

Сфера, описанная около треугольной призмы

В режиме слайдов ответы и решения появляются после кликанья мышкой

Найдите радиус сферы, описанной около правильной призмы, все ребра которой равны 1.

Около правильной треугольной призмы, сторона основания которой равна 1, описана сфера радиуса 2. Найдите высоту призмы.

Следовательно, h = AA 1 = 2 AO =

Около правильной треугольной призмы, высота которой равна 1, описана сфера радиуса 1. Найдите сторону основания призмы.

Найдите радиус сферы, описанной около прямой треугольной призмы, в основании которой прямоугольный треугольник с катетами, равными 1, и высота призмы равна 2.

Решение. Радиус сферы равен половине диагонали A 1 C прямоугольника ACC 1 A 1 .

Сфера, описанная около правильной шестиугольной призмы

В режиме слайдов ответы и решения появляются после кликанья мышкой

Найдите радиус сферы, описанной около правильной шестиугольной призмы, все ребра которой равны 1.

Сфера, описанная около правильной четырехугольной пирамиды

В режиме слайдов ответы и решения появляются после кликанья мышкой

Найдите радиус сферы, описанной около правильной четырехугольной пирамиды, все ребра которой равны 1.

Сфера, описанная около правильной шестиугольной пирамиды

В режиме слайдов ответы и решения появляются после кликанья мышкой

Найдите радиус сферы, описанной около правильной 6-угольной пирамиды, ребра основания которой равны 1, а боковые ребра — 2.

Решение. Треугольник SAD – равносторонний со стороной 2. Радиус R описанной сферы равен радиусу окружности, описанной около треугольника SAD . Следовательно,

Сфера, описанная около октаэдра

В режиме слайдов ответы и решения появляются после кликанья мышкой

Найдите радиус сферы, описанной около единичного октаэдра.

Решение. Радиус R описанной сферы равен половине диагонали квадрата ABCD со стороной 1. Следовательно,

Сфера, описанная около икосаэдра

В режиме слайдов ответы и решения появляются после кликанья мышкой

Найдите радиус сферы, описанной около единичного икосаэдра.

Решение. В прямоугольнике ABCD AB = CD = 1, BC и AD – диагонали правильных пятиугольников со сторонами 1. Следовательно,

Искомый радиус равен половине этой диагонали, т.е.

Сфера, описанная около додекаэдра

Найдите радиус сферы, описанной около единичного додекаэдра.

Решение. ABCDE – правильный пятиугольник со стороной

В прямоугольнике ACGF AF = CG = 1, AC и FG – диагонали пятиугольника ABCDE и, следовательно, AC = FG =

равен половине этой диагонали, т.е.

Сфера, описанная около усеченного тетраэдра

На рисунке изображен усеченный тетраэдр, получаемый отсечением от углов правильного тетраэдра треугольных пирамид, гранями которого являются правильные шестиугольники и треугольники. Найдите радиус сферы, описанной около усеченного тетраэдра, ребра которого равны 1.

Сфера, описанная около усеченного куба

На рисунке изображен усеченный куб, получаемый отсечением от углов куба треугольных пирамид, гранями которого являются правильные восьмиугольники и треугольники. Найдите радиус сферы, описанной около усеченного куба, ребра которого равны 1.

Сфера, описанная около усеченного октаэдра

На рисунке изображен усеченный октаэдр, получаемый отсечением от углов октаэдра треугольных пирамид, гранями которого являются правильные шестиугольники и треугольники. Найдите радиус сферы, описанной около усеченного октаэдра, ребра которого равны 1.

Сфера, описанная около усеченного икосаэдра

На рисунке изображен усеченный икосаэдр, получаемый отсечением от углов икосаэдра пятиугольных пирамид, гранями которого являются правильные шестиугольники и пятиугольники. Найдите радиус сферы, описанной около усеченного икосаэдра, ребра которого равны 1.

Сфера, описанная около усеченного додекаэдра

На рисунке изображен усеченный додекаэдр, получаемый отсечением от углов додекаэдра треугольных пирамид, гранями которого являются правильные десятиугольники и треугольники. Найдите радиус сферы, описанной около усеченного додекаэдра, ребра которого равны 1.

Сфера, описанная около кубооктаэдра

Найдите радиус сферы, описанной около единичного кубооктаэдра

Решение. Напомним, что кубооктаэдр получается из куба отсечением правильных треугольных пирамид с вершинами в вершинах куба и боковыми ребрами, равными половине ребра куба. Если ребро октаэдра равно 1, то ребро соответствующего куба равно Радиус описанной сферы равен расстоянию от центра куба до середины его ребра, т.е. равен 1.

Сфера, описанная около икосододекаэдра

Сфера, описанная около усеченного кубооктаэдра

Сфера, описанная около усеченного икосододекаэдра

Источник