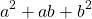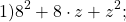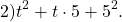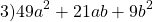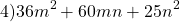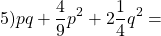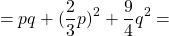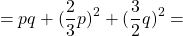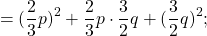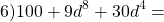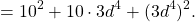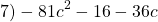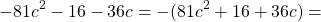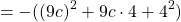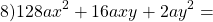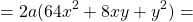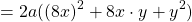Куб одночлена неполный квадрат суммы или разности одночленов якласс

Формулы сокращённого умножения

При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.

Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.

Обратите внимание, что a и b в формулах сокращённого умножения могут быть как числами, так и выражениями.

Разложение формул сокращенного умножения

Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.

Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:

Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

Неполный квадрат суммы

это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:

которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.

Неполный квадрат разности

это квадрат разности, который также называется полным квадратом разности относительно выражения:

которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.

Источник

Неполный квадрат суммы

Неполный квадрат суммы в алгебре встречается в качестве составной части формулы разности кубов. Важно при преобразовании многочленов научиться видеть неполный квадрат и не путать его с полным квадратом суммы.

Неполный квадрат суммы — это сумма трех слагаемых, два из которых являются квадратами некоторых выражений, а третье равно произведению этих выражений.

У неполного квадрата суммы, в отличие от полного, произведение выражений не удваивается.

С помощью букв неполный квадрат суммы можно записать так:

Примеры неполных квадратов —

На практике квадраты и произведение записаны в свернутом виде, поэтому, чтобы понять, является ли выражение полным либо неполным квадратом суммы, его надо проанализировать. На первых шагах изучения темы формулы имеет смысл подробно расписывать, в дальнейшем — делать это устно.

Как определить, является ли некоторое выражение неполным квадратом суммы?

Признаки неполного квадрата суммы

1) Выражение состоит ровно из трех положительных слагаемых.

2) Два слагаемых представляют собой квадраты некоторых выражений.

3) Третье слагаемое равно произведению этих двух выражений.

49y²=(7y)², 9b²=(3b)². Проверяем, равно ли третье слагаемое произведению 7y и 3b: 7y∙3b=21ab — да, равно. Значит, это выражение является неполным квадратом суммы.

С помощью схемы это можно записать так:

36m²=(6m)², 25n²=(5n)². Проверяем, равно ли третье слагаемое произведению 6m и 5n: 6m∙5n=30mn≠60mn. Значит, это выражение не является неполным квадратом суммы (60mn=2∙6m∙5n, то есть здесь есть полный квадрат суммы).

Слагаемые в выражении могут стоять в произвольном порядке (не обязательно в соответствии с формулой).

Иногда выражение, не являющееся неполным квадратом суммы, может быть к нему приведено. Например,

Здесь все три слагаемые — с «-«, то есть это выражение квадратом суммы быть не может. А что, если вынести «минус» за скобки? При этом знак каждого слагаемого в скобках изменится на противоположный:

В этом случае в скобках получили неполный квадрат суммы.

В скобках получили неполный квадрат суммы.

Умение раскладывать многочлены на множители и преобразовывать выражения, в том числе, содержащие разность кубов, в алгебре — обязательно.

Источник

Что такое неполный квадрат суммы? Как решили №33.11? Поделитесь гдз алгебра 7 класс Мордкович!

Запишите разность и неполный квадрат суммы одночленов:
a) k и l; б) 5а 2 и b 2 ; в) 3р и 2m; г) 4s и 3t 2 .

Вот решение
а) k 2 — l 2 ; k2 + kl + l 2 ; б) 5a 2 — b 2 ; 25a 4 + 5a 2 b 2 + b 4 ; в) 3p — 2m; 9p 2 — 6pm + 4m 2 ; г) 4s — 3t 2 ; 16s 2 -12st 2 + 9t4

Разложите многочлен на множители:
а) 7kn — 6k — 14n + 12; в) 9m2 — 9mn — 5m + 5n;
б) 7х + 7а — 6ах — 5а2; ( Подробнее. )

Решите уравнение:
●32.20. а) х2 — 3x + 2 = 0; в) х2 — 6x + 8 = 0;
б) x2 + 8х + 15 = 0; г) x2 ( Подробнее. )

В приведённых ниже предложениях из прочитанного текста пронумерованы все запятые. Выпишите цифры, обозначающие запятые при вводной ( Подробнее. )

1. Через середину М сторони АВ трикутника АВС проведено площину, яка паралельна, прямій АС і перетинає сторону ВС у точці N. Довести NM ( Подробнее. )

Источник

Сложение и вычитание одночленов

Сложить одночлены или вычесть один одночлен из другого можно только в том случае, если одночлены являются подобными. Если одночлены не подобные, в этом случае сложение одночленов можно записать в виде суммы, а вычитание в виде разности.

Подобные одночлены

Подобные одночлены — одночлены, которые состоят из одних и тех же букв, но могут иметь разные или одинаковые коэффициенты (числовые множители). Одинаковые буквы в подобных одночленах должны иметь одинаковые показатели степени. Если у одной и той же буквы в разных одночленах степени не совпадают, то такие одночлены нельзя назвать подобными:

5ab 2 и -7ab 2 — подобные одночлены ;

5a 2 b и 5ab — не подобные одночлены .

Обратите внимание, что последовательность букв в подобных одночленах может не совпадать. Также одночлены могут быть представлены в виде выражения, которое можно упростить. Поэтому, прежде чем приступать к определению, подобны ли данные одночлены, или нет, стоит привести одночлены к стандартному виду. Например, возьмём два одночлена:

Оба одночлена находятся в нестандартном виде, поэтому будет нелегко определить, являются ли они подобными. Чтобы это узнать, приведём одночлены к стандартному виду:

Теперь сразу видно, что данные одночлены являются подобными.

Два подобных одночлена, отличающиеся только знаком, называются противоположными. Например:

5a 2 bc и -5a 2 bc — противоположные одночлены.

Приведение подобных одночленов — это упрощение выражения, содержащего подобные одночлены, путём их сложения. Сложение подобных одночленов производится по правилам приведения подобных слагаемых.

Сложение одночленов

Чтобы сложить одночлены, надо:

1. Составить сумму, записав все слагаемые одно за другим.
2. Привести все одночлены к стандартному виду.
3. Раскрыть скобки, если они есть в выражении.
4. Привести подобные слагаемые. Для этого нужно:
   1. сложить их численные множители;
   2. после получившегося коэффициента дописать буквенные множители без изменений.

Пример 1. Сложить одночлены 12ab, -4a 2 b и -5ab.

Решение: Составим сумму одночленов:

Все одночлены находятся в стандартном виде. Значит, можно приступить к раскрытию скобок. Правила раскрытия скобок смотрите тут.

Теперь надо определить, есть ли среди слагаемых подобные одночлены и, если они есть, сделать приведение:

Пример 2. Сложить одночлены 5a 2 bc и -5a 2 bc.

Решение: Составим сумму одночленов:

Эти два одночлена являются противоположными, то есть, отличаются только знаком. Значит, если мы сложим их численные множители, то получим нуль:

Следовательно, при сложении противоположных одночленов в результате получается нуль.

Общее правило сложения одночленов:

Чтобы сложить несколько одночленов, следует записать все слагаемые одно за другим с сохранением их знаков, отрицательные одночлены надо заключить в скобки и сделать приведение подобных слагаемых (подобных одночленов).

Вычитание одночленов

Чтобы произвести вычитание одночленов, надо:

1. Составить разность, записав все одночлены один за другим, разделяя их знаком — (минус).
2. Привести все одночлены к стандартному виду.
3. Раскрыть скобки, если они есть в выражении.
4. Сделать приведение подобных одночленов, то есть:
   1. сложить их численные множители,
   2. после получившегося коэффициента дописать буквенные множители без изменений.

Пример. Найти разность одночленов 8ab 2 , -5a 2 b и —ab 2 .

Решение: Составим разность одночленов:

Все одночлены находятся в стандартном виде. Значит, можно приступить к раскрытию скобок. Правила раскрытия скобок смотрите тут.

Теперь надо определить, есть ли среди одночленов подобные и, если они есть, сделать приведение:

Общее правило вычитания одночленов:

Для вычитания одного одночлена из другого следует к уменьшаемому одночлену приписать вычитаемый одночлен с противоположным знаком и сделать приведение подобных одночленов.

Источник