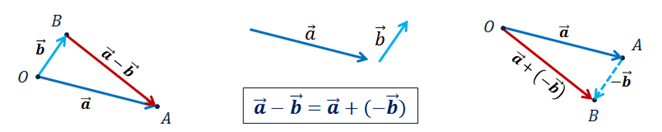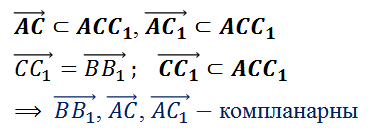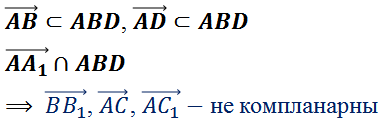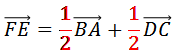Компланарные векторы в кубе примеры

Компланарность векторов. Условия компланарности векторов.

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Условия компланарности векторов

Примеры задач на компланарность векторов

Решение: найдем смешанное произведение векторов

a · [ b × с ] =	1	2	3	=
	1	1	1
	1	2	1

= 1·1·1 + 1·1·2 + 1·2·3 — 1·1·3 — 1·1·2 — 1·1·2 = 1 + 2 + 6 — 3 — 2 — 2 = 2

Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.

Решение: найдем смешанное произведение векторов

a · [ b × с ] =	1	1	1	=
	1	3	1
	2	2	2

= 1·2·3 + 1·1·2 + 1·1·2 — 1·2·3 — 1·1·2 — 1·1·2 = 6 + 2 + 2 — 6 — 2 — 2 = 0

Ответ: вектора компланарны так, как их смешанное произведение равно нулю.

Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования

из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3

	1	1	1
	1 — 1	2 — 1	0 — 1		0	1	-1
	0	-1	1		0	-1	1
	3 — 3	3 — 3	3 — 3		0	0	0

к 3-тей строке добавим 2-рую

1 1 1 0 1 -1 0 1 -1 0 + 0 -1 + 1 1 + (-1) 0 0 0 3 — 3 3 — 3 3 — 3 0 0 0

Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.

Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.

Источник

Компланарные векторы

Вы будете перенаправлены на Автор24

Понятие компланарности векторов

Для начала рассмотрим, какие вектора называются компланарными.

Два вектора, которые параллельны одной плоскости называются компланарными.

Рассмотри, компланарны ли векторы a, b и c на следующем примере. Пусть нам даны три вектора $\overrightarrow,\ \overrightarrow$ и $\overrightarrow$. Тогда

Пары векторов $\overrightarrow,\ и\ \overrightarrow$, $\overrightarrow$ и $\overrightarrow$ и $\overrightarrow$ и $\overrightarrow$ компланарны между собой.

Если два из этих векторов, к примеру $\overrightarrow,\ и\ \overrightarrow$, коллинеарны, то векторы $\overrightarrow,\ \overrightarrow$ и $\overrightarrow$ компланарны.

Если $\overrightarrow,\ \overrightarrow$ и $\overrightarrow$ лежат в одной плоскости, то они компланарны.

Для дальнейшего рассмотрения напомним следующую теорему.

Произвольный вектор $\overrightarrow

$ можно разложить по двум неколлинеарным векторам $\overrightarrow,\ $ и $\overrightarrow$ с единственными коэффициентами разложения, то есть

Теоремы, связанные с условием компланарности трех векторов

Если один из трех данных векторов можно разложить по двум другим векторам, то есть

Доказательство.

Здесь возможны два случая.

Теорема доказана.

Готовые работы на аналогичную тему

Доказательство.

\[\overrightarrow=\alpha \overrightarrow+\beta \ \overrightarrow\]

Причем это разложение единственно.

Которое также единственно.

Теорема доказана.

Признак и критерий компланарности векторов

Рисунок 1. Условие компланарности векторов. Автор24 — интернет-биржа студенческих работ

Пример задачи

Пусть нам дан куб $ABCDA_1B_1C_1D_1$. Разложите вектор $\overrightarrow$ по векторам $\overrightarrow\ и\ \overrightarrow$.

Рисунок 2. Разложение по векторам. Автор24 — интернет-биржа студенческих работ

Так как плоскости $(ABC)$ и $<(A>_1B_1C_1)$ параллельны, и векторы $\overrightarrow$, $\overrightarrow\ и\ \overrightarrow$ параллельны, следовательно, по определению являются компланарными. Тогда, по теореме 1, вектор $\overrightarrow$ можно разложить по векторам $\overrightarrow\ и\ \overrightarrow$ единственным образом.

Используя свойства сложения двух векторов, получим

Ответ: $\overrightarrow+\overrightarrow$.

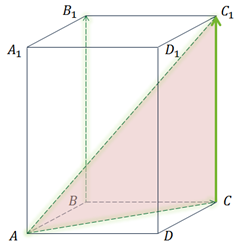
Пусть нам дан параллелепипед. Найти тройки компланарных векторов, изображенных в параллелепипеде на рисунке ниже.

Рисунок 3. Параллелепипед. Автор24 — интернет-биржа студенческих работ

Так как векторы $\overrightarrow,\ \overrightarrow$ и $\overrightarrow$ лежат в плоскости $(BOA)$ то эти векторы являются компланарными.

Так как векторы $\overrightarrow,\ \overrightarrow$ и $\overrightarrow<_1>$ лежат в плоскости $(BOC)$ то эти векторы являются компланарными.

Так как векторы $\overrightarrow,\ \overrightarrow$ и $\overrightarrow$ лежат в плоскости $(COE)$ то эти векторы являются компланарными.

Доказать, что векторы с координатами $\left(1,\ 13,\ 2\right),\ \left(3,\ -5,\ 2\right)и\ (5,-1,4)$ компланарны.

Применим признак компланарности трех векторов.

Рисунок 4. Нахождение определителя. Автор24 — интернет-биржа студенческих работ

Следовательно, это векторы компланарны, ч. т. д.

Источник

Компланарные векторы и условие компланарности

В данной статье мы рассмотрим такие темы, как:

• определение компланарных векторов;
• условия компланарности векторов;
• примеры задач на компланарность векторов.

Определение компланарных векторов

Компланарные векторы — это векторы, которые параллельны одной плоскости или лежат на одной плоскости.

Два любых вектора всегда компланарны, поскольку всегда можно найти плоскости параллельные 2-м произвольным векторам.

Условия компланарности векторов

• Для 3-х векторов выполняется условие: если смешанное произведение 3-х векторов равно нулю, то эти три вектора компланарны.
• Для 3-х векторов выполняется условие: если три вектора линейно зависимы, то они компланарны.
• Для n-векторов выполняется условие: если среди векторов не более 2-х линейно независимых векторов, то они компланарны.

Примеры решения задач на компланарность векторов

Исследуем на компланарность векторы

a ¯ = ( 1 ; 2 ; 3 ) , b = ( 1 ; 1 ; 1 ) и c ¯ = ( 1 ; 2 ; 1 )

Векторы будут являться компланарными, если их смешанное произведение равно нулю, поэтому вычисляем смешанное произведение заданных векторов. Для этого составляем определитель, по строкам которого записываются координаты векторов-сомножителей:

( a ¯ , b ¯ , c ¯ ) = 1 2 3 1 1 1 1 2 1 = = 1 × 1 × 1 + 1 × 2 × 3 + 2 × 1 × 1 — 1 × 1 × 3 — 2 × 1 × 1 — 1 × 2 × 1 = 2 ≠ 0

Отсюда следует, что смешанное произведение не равняется нулю, поэтому векторы не являются компланарными.

Ответ: векторы не являются компланарными.

a ¯ = ( 1 ; — 1 ; 2 ) , b = ( 0 ; 1 ; — 1 ) и c ¯ = ( 2 ; — 2 ; 4 ) компланарны.

Находим смешанное произведение данных векторов:

( a ¯ , b ¯ , c ¯ ) = 1 — 1 2 0 1 — 1 2 — 2 4 = = 1 × 1 × 4 + 0 × ( — 2 ) × 2 + ( — 1 ) × ( — 1 ) × × 2 — 2 × 1 × 2 — ( — 2 ) × ( — 1 ) × 1 — 0 × ( — 1 )

Из данного примера видно, что смешанное произведение равняется нулю.

Ответ: векторы являются компланарными.

Проверим, компланарны ли векторы

Необходимо найти количество линейно независимых векторов: записываем значения векторов в матрицу и выполняем элементарные преобразования:

Из 2-ой строки вычитаем 1-ю, из 4-ой вычитаем 1-ю, умноженную на 3:

1 1 1 1 — 1 2 — 1 0 — 1 0 — 1 1 3 — 3 3 — 3 3 — 3

1 1 1 0 1 — 1 0 — 1 1 0 0 0

К 3-ей строке прибавляем 2-ю:

1 1 1 0 1 — 1 0 + 0 — 1 + 1 1 + ( — 1 ) 3 — 3 3 — 3 3 — 3

Поскольку в матрице только две ненулевые строки, делаем вывод, что среди них всего два линейно независимых вектора.

Ответ: векторы являются компланарными, поскольку среди них всего два линейно независимых вектора.

Источник

Компланарные векторы

Урок 37. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока «Компланарные векторы»

Ранее мы ввели понятие вектора в пространстве, понятие равных векторов, правила сложения и вычитания векторов, а также произведение вектора на число.

И все теоретические аспекты векторов в пространства практически совпадают с теорией векторов на плоскости. За исключением правила многоугольника сложения нескольких векторов. Многоугольник сложения в пространстве может быть и пространственным, то есть не все его вершины лежат в одной плоскости.

Сегодня мы с вами познакомимся с существенным и одним из главных отличий векторов на плоскости и векторов в пространстве. Мы введём понятие компланарных векторов.

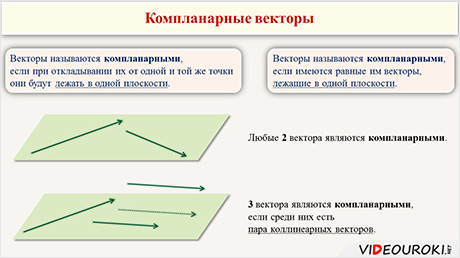
Определение. Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

Но в связи с тем, что от любой точки пространства можно отложить вектор равный данному, и притом только один, можно это определение переформулировать так.

Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

Понятно, что любые два вектора всегда будут компланарными, ведь через них можно провести прямые, а через две прямые всегда можно провести единственную плоскость.

Если же рассмотреть три вектора, то они могут быть как компланарными, так и некомпланарными.

Компланарными они будут в том случае, когда среди них есть пара коллинеарных векторов.

Тогда через один из коллинеарных векторов и вектор не коллинеарный ему можно провести плоскость. А для второго из коллинеарных векторов легко изобразить равный в этой плоскости.

Так мы получаем, что два вектора всегда будут компланарными, а три вектора будут компланарными, если среди них есть пара коллинеарных векторов.

прямоугольный параллелепипед.

а) , ,

б) , ,

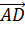
Первой рассмотрим тройку .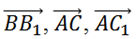

Через векторы и проведём плоскость ACC₁.

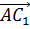
Рассмотрим следующую тройку векторов. .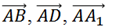

В этом задании мы, пользуясь определением, выяснили компланарны данные тройки векторов или нет.

Помимо определения компланарных векторов есть ещё и признак компланарности трёх векторов.

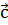
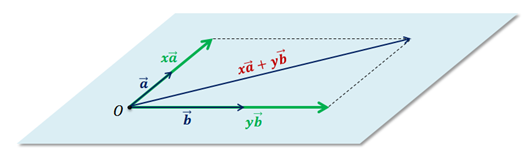
Если вектор можно разложить по векторам и , то есть представить его в таком виде , где x и y некоторые числа. То векторы , и компланарны.

Рассмотрим два неколлинеарных вектора и , отложим их от некоторой точки О. Далее проведём через них плоскость.

Очевидно, что в этой же плоскости лежат векторы x и y.

По правилу параллелограмма построим вектор суммы векторов x и y. Полученный вектор суммы равен вектору . А по рисунку становится понятно, что векторы , и действительно лежат в одной плоскости, а значит, они компланарны.

Так мы доказали признак компланарности трёх векторов. Но справедливо и обратное утверждение, которое можно считать свойством трёх компланарных векторов.

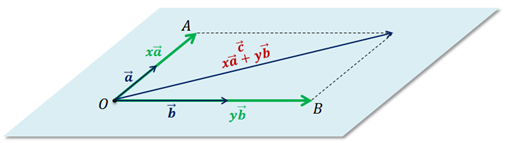
Если векторы , и компланарны, а векторы , не коллинеарны, то вектор можно разложить по векторам и , причём коэффициенты разложения определяются единственным образом.

Итак, воспользуемся тем, векторы компланарны, то есть лежат в одной плоскости. А из курса планиметрии известно, что любой вектор плоскости можно разложить по двум неколлинеарным векторам. Как раз векторы и являются такими по условию.

Тогда отложим векторы , и от некоторой точки О плоскости.

Вектор равен сумме векторов и , каждый из которых коллинеарен векторам и соответственно. Опираясь на коллинеарность, можем вектор представить в виде произведения вектора и некоторого числа x, а вектор — в виде произведения вектора и некоторого числа y.

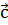
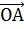
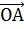
Отсюда получаем, что вектор равен сумме произведений вектора на число x и вектора на число y.

Тем самым мы смогли разложить вектор по векторам и .

Что и требовалось доказать.

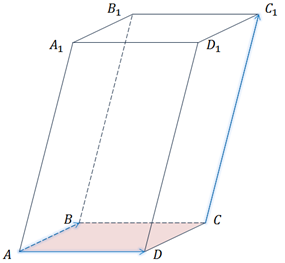
Для параллелепипеда ABCDA₁B₁C₁D₁ среди данных троек векторов найти компланарные.

Первой рассмотрим тройку векторов .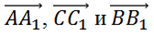

Все эти векторы коллинеарны, так как являются противоположными рёбрами параллелепипеда. А для компланарности трёх векторов достаточно коллинеарности хотя бы двух из них (в начале урока мы рассматривали такой случай). Поэтому можно утверждать, что данные векторы компланарны.

Далее рассмотрим векторы , и .

Векторы и лежат в одной плоскости, а вектор пересекает её. Поэтому можно сказать, что данные векторы не компланарны.

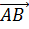
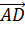
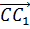
Следующей рассмотрим тройку векторов , и .

Среди них есть пара коллинеарных векторов, и . А значит, векторы данной тройки будут компланарны.

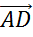
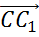
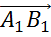
Осталось рассмотреть тройку векторов , и .

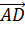
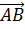
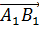
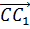
В плоскости ABCD лежит вектор . И вектор , равен вектору . Но для вектора в этой плоскости не найдётся равный, так как он пересекает её. Значит, векторы данной тройки не будут являться компланарными.

Так, пользуясь определением, мы нашли две тройки компланарных векторов.

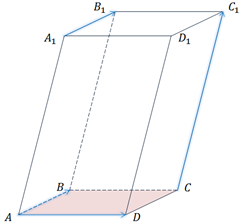
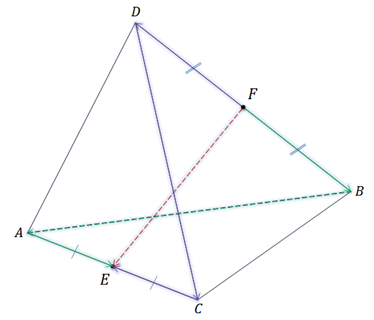
Задача. тетраэдр. Точки и — середины сторон и . Доказать, что . Компланарны ли векторы , и ?

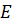
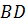
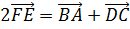
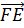
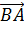
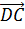
Итак, сначала проведём доказательство.

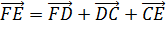
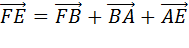
Пользуясь правилом многоугольника сложения нескольких векторов в пространстве, можно записать, что . С другой стороны вектор .

Сложим покомпонентно эти два равенства.

Векторы и , а также и противоположны, ведь их длины равны и они противоположно направлены. А значит, каждая из этих сумм равна нулевому вектору.

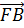
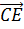
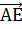
Тогда мы получаем, что .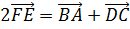

Что и требовалось доказать.

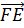
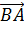
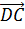
Теперь ответим на вопрос, компланарны ли векторы , и .

Разделим обе его части равенства, доказанного выше, на 2.

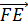
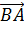
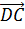
Так мы записали разложение вектора по векторам и , где оба коэффициента разложения равны .

Тогда по признаку компланарных векторов, данные векторы компланарны.

Подведём итоги нашего урока.

Сегодня мы ввели понятие компланарных векторов.

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

На практике удобнее использовать такую формулировку: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

Так же мы выяснили, что любые два вектора всегда компланарны, а вот три вектора могут быть как компланарными, так и не компланарными.

В связи с этим мы доказали признак компланарности векторов.

Если вектор можно разложить по неколлинеарным векторам и , то векторы , и компланарны.

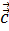
Справедливо также и обратное утверждение.

Если векторы , и компланарны, а векторы и не коллинеарны, то вектор можно разложить по векторам и , причём коэффициенты разложения определяются единственным образом.

Источник