Колоколообразная зависимость плотности вероятности от случайной величины соответствует

Функция распределения плотности вероятностей и ее свойства. Функция плотности вероятности. Функция плотности. Подробно.

Функция распределения плотности вероятностей и ее свойства. Функция плотности вероятности. Функция плотности. Подробно.

• Из формулы P <Α ≤ X x f(t)dt.
• Действительно, так как по определению f(x)=F'(x), то F(x) является первообразной функцией по отношению к плотности распределения f(x). Следовательно,
• _-∞∫ ∞ f(t)dt=F(t)_-∞ι x =F(x)-F(-∞)=F(x)-0=F(x.)

3. Вероятность попадания случайной величины в заданный интервал [Α ; Β] равна:

• P <Α≤X β f(t)dt.
• Действительно, в соответствии с формулой Ньютона-Лейбница этот определенный интеграл равен F(Β)-F(Α). По 3-му свойству функции распределения вероятностей эта разность и представляет собой вероятность P <Α≤X ∞ f(t)dt=1 .

Равенство _-∞∫ ∞ f(t)dt=1 представляет условие нормировки вероятностей для непрерывных случайных величин. По смыслу данный интеграл есть не что иное, как F(∞)=1. Условие нормировки вероятностей часто используется для определения неизвестного параметра закона распределения.

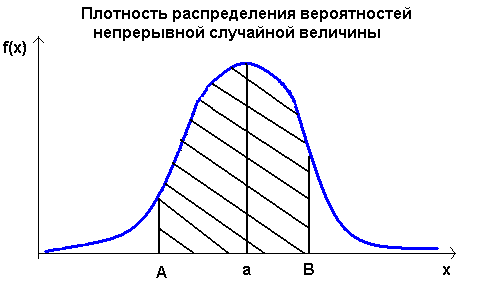
Для иллюстрации геометрического смысла перечисленных свойств приведем пример графика плотности распределения вероятностей. Для большей наглядности на рис. представлен также график соответствующей функции распределения вероятностей.

Вся кривая плотности распределения вероятностей располагается выше оси 0Х (свойство1), причем максимум плотности достигается в точке х=а, в которой функция распределения вероятностей имеет наибольшую крутизну. Вероятность попадания случайной величины в интервал [Α ; Β] численно равна площади криволинейной трапеции, построенной на этом интервале как на основании и ограниченной сверху графиком плотности распределения (заштрихованная на рисунке область). Площадь всей криволинейной трапеции, заключенной между осью 0Х и графиком плотности распределения, всегда равна единице. Любая функция, удовлетворяющая перечисленным выше свойствам, может быть плотностью распределения некоторой непрерывной случайной величины.

Источник

Нормальное распределение непрерывной случайной величины

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Нормальное распределение: теория и практика

Примерами случайных величин, распределённых по нормальному закону, являются рост человека, масса вылавливаемой рыбы одного вида. Нормальность распределения означает следующее: существуют значения роста человека, массы рыбы одного вида, которые на интуитивном уровне воспринимаются как «нормальные» (а по сути — усреднённые), и они-то в достаточно большой выборке встречаются гораздо чаще, чем отличающиеся в бОльшую или меньшую сторону.

Нормальное распределение вероятностей непрерывной случайной величины (иногда — распределение Гаусса) можно назвать колоколообразным из-за того, что симметричная относительно среднего функция плотности этого распределения очень похожа на разрез колокола (красная кривая на рисунке выше).

Вероятность встретить в выборке те или иные значение равна площади фигуры под кривой и в случае нормального распределения мы видим, что под верхом «колокола», которому соответствуют значения, стремящиеся к среднему, площадь, а значит, вероятность, больше, чем под краями. Таким образом, получаем то же, что уже сказано: вероятность встретить человека «нормального» роста, поймать рыбу «нормальной» массы выше, чем для значений, отличающихся в бОльшую или меньшую сторону. В очень многих случаях практики ошибки измерения распределяются по закону, близкому к нормальному.

Если копнуть глубже, то нормальное распределение можно найти в распределении многих показателях в системах связи (сигналы, шумы, помехи и другие), под нормальное распределение подгоняют многие финансовые показатели. Хотя следует подчеркнуть, что именно подгоняют, поскольку признаки нормальности в этих случаях часто бывают смещены.

Остановимся ещё раз на рисунке в начале урока, на котором представлена функция плотности нормального распределения. График этой функции получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. На ней столбцы гистограммы представляют собой интервалы значений выборки, распределение которых близко (или, как принято говорить в статистике, незначимо отличаются от) к собственно графику функции плотности нормального распределения, который представляет собой кривую красного цвета. На графике видно, что эта кривая действительно колоколообразная.

Нормальное распределение во многом ценно благодаря тому, что зная только математическое ожидание непрерывной случайной величины и стандартное отклонение, можно вычислить любую вероятность, связанную с этой величиной.

Нормальное распределение имеет ещё и то преимущество, что один из наиболее простых в использовании статистических критериев, используемых для проверки статистических гипотез — критерий Стьюдента — может быть использован только в том случае, когда данные выборки подчиняются нормальному закону распределения.

Что влияет на график плотности нормального распределения

Чуть далее мы разберем довольно ужасную на первый взгляд формулу функции плотности нормального распределения. А пока остановимся на важнейших параметрах, связанных с этой формулой, которые влияют на вид графика плотности нормального распределения.

Стандартное отклонение (σ), может принимать значения от нуля до плюс бесконечности. При увеличении стандартного отклонения график плотности нормального распределения становится более растянутым вдоль оси Ox, а при уменьшении — наоборот, сжимается. Это показано на графике снизу.

Математическое ожижание или среднее (μ). При его увеличении график плотности нормального распределения сдвигается вправо вдоль оси Ox, а при уменьшении — влево. При нулевом значении график центрирован вокруг x=0. На графике снизу показаны две кривые нормального распределения с одинаковыми стандартными отклонениями, но разными значениями математического ожидания. Видно, что та кривая, которая относится к μ=3, смещена вправо.

Коэффициент асимметрии (β 1 ). Если он равен нулю, то график плотности нормального распределения симметричен относительно среднего. Если он отличен от нуля, то распределение случайной величины несимметрично, причем, если коэффициент положителен, то правый хвост длиннее, а если отрицателен, то длиннее левый хвост. Это показано на графике снизу.

Коэффициент эксцесса (β 2 ). Характеризует остроту вершины графика плотности нормального распределения. Чем больше значение коэффициента, тем острее вершина. Это показано на графике снизу.

Подробнее о функции плотности нормального распределения

Функцию плотности нормального распределения непрерывной случайной величины можно найти по формуле:

,

где x — значение изменяющейся величины, — среднее значение, — стандартное отклонение, e=2,71828. — основание натурального логарифма, =3,1416.

Свойства функции плотности нормального распределения

• для всех значений аргумента функция плотности положительна;
• если аргумент стремится к бесконечности, то функция плотности стреится к нулю;
• функция плотности симметрична относительно среднего значения: ;
• наибольшее значение функции плотности — у среднего значения: ;
• кривая функции плотности выпукла в интервале и вогнута на остальной части;
• мода и медиана нормального распределения совпадает со средним значением;
• при нормальном распределении коэффициенты ассиметрии и эксцесса равны нулю (подробнее рассмотрим это свойство в следующем параграфе о приближенном методе проверки нормальности распределения).

Повторим знания о графиках функции плотности. Изменения среднего значения перемещают кривую функции плотности нормального распределения в направлении оси Ox. Если возрастает, кривая перемещается вправо, если уменьшается, то влево.

Если меняется стандартное отклонение, то меняется высота вершины кривой. При увеличении стандартного отклонения вершина кривой находится выше, при уменьшении — ниже.

Вероятность попадания значения нормально распределённой случайной величины в заданный интервал

Уже в этом параграфе начнём решать практические задачи, смысл которых обозначен в заголовке. Разберём, какие возможности для решения задач предоставляет теория. Отправное понятие для вычисления вероятности попадания нормально распределённой случайной величины в заданный интервал — интегральная функция нормального распределения.

Интегральная функция нормального распределения:

.

Однако проблематично получить таблицы для каждой возможной комбинации среднего и стандартного отклонения. Поэтому одним из простых способов вычисления вероятности попадания нормально распределённой случайной величины в заданный интервал является использование таблиц вероятностей для стандартизированного нормального распределения.

Стандартизованным или нормированным называется нормальное распределение, среднее значение которого , а стандартное отклонение .

Функция плотности стандартизованного нормального распределения:

.

Интегральная функция стандартизованного нормального распределения:

.

На рисунке ниже представлена интегральная функция стандартизованного нормального распределения, график которой получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. Собственно график представляет собой кривую красного цвета, а значения выборки приближаются к нему.

Для увеличения рисунка можно щёлкнуть по нему левой кнопкой мыши.

Стандартизация случайной величины означает переход от первоначальных единиц, используемых в задании, к стандартизованным единицам. Стандартизация выполняется по формуле

.

На практике все возможные значения случайной величины часто не известны, поэтому значения среднего и стандартного отклонения точно определить нельзя. Их заменяют средним арифметическим наблюдений и стандартным отклонением s. Величина z выражает отклонения значений случайной величины от среднего арифметического при измерении стандартных отклонений.

Открытый интервал

Таблица вероятностей для стандартизированного нормального распределения, которая есть практически в любой книге по статистике, содержит вероятности того, что имеющая стандартное нормальное распределение случайная величина Z примет значение меньше некоторого числа z. То есть попадёт в открытый интервал от минус бесконечности до z. Например, вероятность того, что величина Z меньше 1,5, равна 0,93319.

Пример 1. Предприятие производит детали, срок службы которых нормально распределён со средним значением 1000 и стандартным отклонением 200 часов.

Для случайно отобранной детали вычислить вероятность того, что её срок службы будет не менее 900 часов.

Решение. Введём первое обозначение:

— искомая вероятность.

Значения случайной величины находятся в открытом интервале. Но мы умеем вычислять вероятность того, что случайная величина примет значение, меньшее заданного, а по условию задачи требуется найти равное или большее заданного. Это другая часть пространства под кривой плотности нормального распределения (колокола). Поэтому, чтобы найти искомую вероятность, нужно из единицы вычесть упомянутую вероятность того, что случайная величина примет значение, меньше заданного 900:

Теперь случайную величину нужно стандартизировать.

Продолжаем вводить обозначения:

x = 900 — заданное значение случайной величины;

μ = 1000 — среднее значение;

σ = 200 — стандартное отклонение.

По этим данным условия задачи получаем:

.

По таблицам стандартизированной случайной величине (границе интервала) z = −0,5 соответствует вероятность 0,30854. Вычтем ее из единицы и получим то, что требуется в условии задачи:

.

Итак, вероятность того, что срок службы детали будет не менее 900 часов, составляет 69%.

Эту вероятность можно получить, используя функцию MS Excel НОРМ.РАСП (значение интегральной величины — 1):

P(X≥900) = 1 — P(X≤900) = 1 — НОРМ.РАСП(900; 1000; 200; 1) = 1 — 0,3085 = 0,6915.

О расчётах в MS Excel — в одном из последующих параграфах этого урока.

Пример 2. В некотором городе среднегодовой доход семьи является нормально распределённой случайной величиной со средним значением 300000 и стандартным отклонением 50000. Известно, что доходы 40 % семей меньше величины A. Найти величину A.

Решение. В этой задаче 40 % — ни что иное, как вероятность того, что случайная величина примет значение из открытого интервала, меньшее определённого значения, обозначенного буквой A.

Чтобы найти величину A, сначала составим интегральную функцию:

μ = 300000 — среднее значение;

σ = 50000 — стандартное отклонение;

x = A — величина, которую нужно найти.

.

По статистическим таблицам находим, что вероятность 0,40 соответствует значению границы интервала z = −0,25 .

Поэтому составляем равенство

Ответ: доходы 40 % семей менее 287300.

Закрытый интервал

Во многих задачах требуется найти вероятность того, что нормально распределённая случайная величина примет значение в интервале от z 1 до z 2 . То есть попадёт в закрытый интервал. Для решения таких задач необходимо найти в таблице вероятности, соответствующие границам интервала, а затем найти разность этих вероятностей. При этом требуется вычитать меньшее значение из большего. Примеры на решения этих распространённых задач — следующие, причём решить их предлагается самостоятельно, а затем можно посмотреть правильные решения и ответы.

Пример 3. Прибыль предприятия за некоторый период — случайная величина, подчинённая нормальному закону распределения со средним значением 0,5 млн. у.е. и стандартным отклонением 0,354. Определить с точностью до двух знаков после запятой вероятность того, что прибыль предприятия составит от 0,4 до 0,6 у.е.

Пример 4. Длина изготавливаемой детали представляет собой случайную величину, распределённую по нормальному закону с параметрами μ=10 и σ=0,071 . Найти с точностью до двух знаков после запятой вероятность брака, если допустимые размеры детали должны быть 10±0,05 .

Подсказка: в этой задаче помимо нахождения вероятности попадания случайной величины в закрытый интервал (вероятность получения небракованной детали) требуется выполнить ещё одно действие.

позволяет определить вероятность того, что стандартизованное значение Z не меньше -z и не больше +z, где z — произвольно выбранное значение стандартизованной случайной величины.

Приближенный метод проверки нормальности распределения

Приближенный метод проверки нормальности распределения значений выборки основан на следующем свойстве нормального распределения: коэффициент асимметрии β 1 и коэффициент эксцесса β 2 равны нулю.

Коэффициент асимметрии β 1 численно характеризует симметрию эмпирического распределения относительно среднего. Если коэффициент асимметрии равен нулю, то среднее арифметрического значение, медиана и мода равны: и кривая плотности распределения симметрична относительно среднего. Если коэффициент асимметрии меньше нуля ( β 1 ), то среднее арифметическое меньше медианы, а медиана, в свою очередь, меньше моды () и кривая сдвинута вправо (по сравнению с нормальным распределением). Если коэффициент асимметрии больше нуля ( β 1 > 0 ), то среднее арифметическое больше медианы, а медиана, в свою очередь, больше моды () и кривая сдвинута влево (по сравнению с нормальным распределением).

Коэффициент эксцесса β 2 характеризует концентрацию эмпирического распределения вокруг арифметического среднего в направлении оси Oy и степень островершинности кривой плотности распределения. Если коэффициент эксцесса больше нуля, то кривая более вытянута (по сравнению с нормальным распределением) вдоль оси Oy (график более островершинный). Если коэффициент эксцесса меньше нуля, то кривая более сплющена (по сравнению с нормальным распределением) вдоль оси Oy (график более туповершинный).

Коэффициент асимметрии можно вычислить с помощью функции MS Excel СКОС. Если вы проверяете один массив данных, то требуется ввести диапазон данных в одно окошко «Число».

Коэффициент эксцесса можно вычислить с помощью функции MS Excel ЭКСЦЕСС. При проверке одного массива данных также достаточно ввести диапазон данных в одно окошко «Число».

Итак, как мы уже знаем, при нормальном распределении коэффициенты асимметрии и эксцесса равны нулю. Но что, если мы получили коэффициенты асимметрии, равные -0,14, 0,22, 0,43, а коэффициенты эксцесса, равные 0,17, -0,31, 0,55? Вопрос вполне справедливый, так как практически мы имеем дело лишь с приближенными, выборочными значениями асимметрии и эксцесса, которые подвержены некоторому неизбежному, неконтролируемому разбросу. Поэтому нельзя требовать строгого равенства этих коэффициентов нулю, они должны лишь быть достаточно близкими к нулю. Но что значит — достаточно?

Требуется сравнить полученные эмпирические значения с допустимыми значениями. Для этого нужно проверить следующие неравенства (сравнить значения коэффициентов по модулю с критическими значениями — границами области проверки гипотезы).

Для коэффициента асимметрии β 1 :

,

— квантиль стандартного нормального распределения уровня ,

— среднеквадратическое отклонение для выборки с числом наблюдений n .

Для коэффициента эксцесса β 2 :

,

— квантиль стандартного нормального распределения уровня ,

— среднеквадратическое отклонение для выборки с числом наблюдений n .

Так как коэффициенты асимметрии и эксцесса могут оказаться и положительными, и отрицательными, то в приближенном методе проверки нормальности распределения используется двусторонний квантиль стандартного нормального распределения; он задаёт интервал, в который случайная величина попадает с определённой вероятностью. Приведём значения двусторонних квантилей стандартного нормального распределения определённых уровней (слева — уровень, справа — значение квантиля):

Например, для выборки с числом наблюдений n = 50 и α = 0,05 , пользуясь этими значениями и ранее приведёнными формулами, можно получить границу области принятия гипотезы для коэффициента асимметрии 0,62 и для коэффициента эксцесса 1,15. Поэтому приведённые ранее примеры эмпирических значений коэффициента асимметрии -0,14, 0,22, 0,43 попадают в область принятия гипотезы. То же самое относится к значениям коэффициента эксцесса 0,17, -0,31, 0,55. Следовательно, если получены такие эмпирические значения, то с вероятностью 95% данные выборки подчиняются нормальному закону распределения.

Нормальное распределение и расчёты в MS Excel

Значения функции плотности f(x) и интегральной функции F(x) нормального распределения можно вычислить при помощи функции MS Excel НОРМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).

MS Excel требует ввести следующие данные:

• x — значение изменяющегося признака;
• среднее значение;
• стандартное отклонение;
• интегральная — логическое значение: 0 — если нужно вычислить функцию плотности f(x) и 1 — если вероятность F(x).

Решим ещё задачи на нормальное распределение

Решить задачу самостоятельно, а затем посмотреть решение

Пример 5. Определить с точностью до двух знаков после запятой вероятность попадания при стрельбе в полосу шириной 3,5 м, если ошибки стрельбы подчиняются нормальному закону распределения со средним значением 0 и σ = 1,9 .

Решим ещё одну задачу вместе

Пример 6. О случайной величине X известно, что она нормально распределена, а вероятности того, что она составит 10 или меньше и больше 25, соответственно и . Найти среднее значение (математическое ожидание) случайной величины и её дисперсию.

Решение. Используем данные в условии задачи вероятности:

Пользуясь статистическими таблицами, находим:

Составляем систему из полученных равенств:

.

Источник