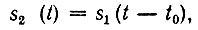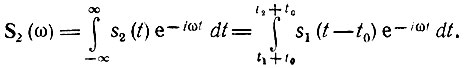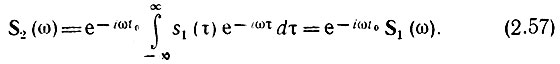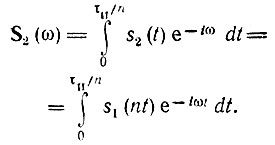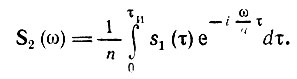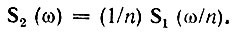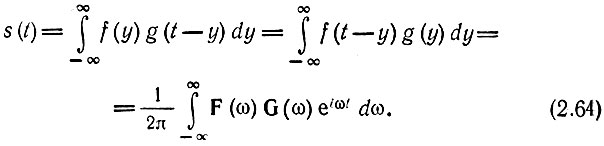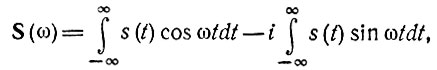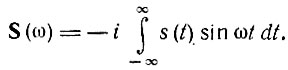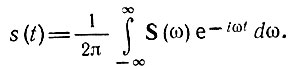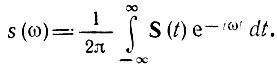Колебания плотности во времени


2.7. Некоторые свойства преобразования Фурье
Между колебанием s(t) и его спектром S(ω) существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием колебания и соответствующим этому преобразованию изменением спектра. Из многочисленных возможных преобразований колебания рассмотрим следующие наиболее важные и часто встречающиеся: сдвиг колебания во времени, изменение масштаба времени, сдвиг спектра колебания по частоте, дифференцирование и интегрирование колебания. Кроме того, будут рассмотрены сложение колебаний, произведение и свертка двух колебаний, а также свойства взаимной обратимости ω и t в преобразованиях Фурье.
1. Сдвиг колебания во времени
Пусть колебание s1(t) произвольной формы существует на интервале времени от t1 до t2 и обладает спектральной плотностью S1(ω). При задержке этого колебания на величину t0 (при сохранении его формы) получим новую функцию времени
существующую на интервале от t1 + t0 до t2 + t0.
Спектральная плотность колебания s2(t) в соответствии с (2.48)
Вводя новую переменную интегрирования τ = t — t0, получаем
Из этого соотношения видно, что сдвиг во времени функции s(t) на величину ±t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt0. Очевидно и обратное положение: если всем составляющим спектра функции s(t) дать фазовый сдвиг θ(ω) = ±ωt0, линейно связанный с частотой ω, то функция сдвигается во времени на величину ±t0.
Амплитудно-частотная характеристика спектра (т. е. модуль спектральной плотности) от положения колебания на оси времени не зависит.
2. Изменение масштаба времени
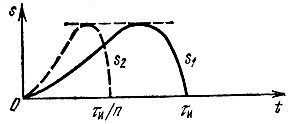
Пусть колебание s1(t), изображенное на рис. 2.12 сплошной линией, подверглось сжатию во времени. Новое сжатое колебание s2(t) (штриховая кривая на рис. 2.12) связано с исходным колебанием соотношением s2(t) = s1(nt), n > 1.
Рис. 2.12. Сжатие сигнала при сохранении его формы и амплитуды
Длительность импульса s2(t) в n раз меньше, чем у исходного импульса, и равна τи/n. Спектральная плотность сжатого импульса
Вводя новую переменную интегрирования τ = nt, получаем
Но интеграл в правой части этого выражения есть не что иное, как спектральная плотность исходного колебания s1(t) при частоте ω/n, т. е. S1(ω/n).
Итак, при сжатии колебания в n раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в n раз. Очевидно, что при растягивании колебаний во времени (т. е. при n * (ω) = F(-ω) — спектральная функция, комплексно-сопряженная функции F(ω).
Совершенно аналогично можно показать, что произведению двух спектров F(ω) G(ω) = S(ω) соответствует функция времени s(t), являющаяся сверткой функций f(t) и g(t):
Последнее выражение особенно широко используется при анализе передачи сигналов через линейные цепи. В этом случае функции времени f(t) и g(t) имеют смысл соответственно входного сигнала и импульсной характеристики цепи (см. § 6.3), a F(ω) и G(ω) — спектральной плотности сигнала и передаточной функции цепи.
7. Взаимная заменяемость ω и t в преобразованиях Фурье
Обратимся к общему выражению (2.48) и выясним характер функции S(ω) для различных функций s(t).
а. Пусть s(t) есть функция, четная относительно t. Переписывая выражение (2.48) в виде
убеждаемся, что при четности s(t) второй интеграл равен нулю, так как произведение s(t) sinωt является функцией, нечетной относительно t, а пределы интегрирования симметричны.
Таким образом, при s(t), четной относительно t, функция S(ω), определяемая первым интегралом, есть функция вещественная и четная относительно ω.
б. Если s(t) нечетна относительно t, то в нуль обращается первый интеграл и
В этом случае S(ω) — нечетная и чисто мнимая функция ω.
в. Если, наконец, s(t) не является четной или нечетной функцией относительно t, то ее можно разложить на две функции: четную s1(t) и нечетную s2(t). При этом S(ω) представляет комплексную функцию, причем действительная ее часть четна, а мнимая нечетна относительно ω.
Из п. а вытекает, что при четной функции s(t) можно произвольно выбирать знак перед t. в обратном преобразовании Фурье [формула (2.49)]; выберем знак минус и запишем формулу (2.49) в виде
Произведем теперь в последнем интеграле замену переменной интегрирования ω на t и параметра t на ω. Тогда левая часть должна быть записана в виде функции от аргумента ω
Но интеграл в последнем выражении можно рассматривать как спектральную плотность новой функции S(t), полученной путем замены ω на t в выражении спектральной плотности колебания s(t).
Обозначим эту новую спектральную плотность через S'(ω). Тогда
Этот результат показывает, что переменные ω и t в преобразованиях Фурье взаимно заменимы: если колебанию (четному) s(t) соответствует спектр S(ω), то колебанию S(t) соответствует спектр 2πs(ω).
Пример применения этого правила приводится в п. 3, § 2.9.
О радиальных колебаниях.
О РАДИАЛЬНЫХ КОЛЕБАНИЯХ ПЛОТНОСТИ В УПРУГОЙ СРЕДЕ
Этой небольшой статьёй я попытаюсь заполнить тот пробел в нашем естествознании, касающийся процессов радиальных колебаний плотности в сплошных упругих средах. Вероятно, эта тема заслуживает более серьёзного рассмотрения, но мне придётся ограничиться в силу некоторых причин лишь общим изложением вопроса.
В качестве упругой среды мы возьмём наше пространство или, как сейчас говорят, физический вакуум. Быть может, главной причиной тому, что вопросы, касающиеся процессов радиальных колебаний плотности в упругих средах, не находили себе места в научной литературе, была та, что подобные процессы уникальны и возможны лишь в единственной среде с уникальной структурой, а именно, физическом вакууме. И прежде чем перейти непосредственно к радиальным колебаниям, остановимся на структуре пространства. Но позволительно спросить: почему вы называете пространство упругой средой, и откуда вы взяли, что вакуум обладает свойством изменять свою плотность? Во-первых, то, что пространство имеет реальную физическую сущность, не меньшую, чем воздух, было установлено ещё в начале нашего века, когда естествознанию под напором опытных фактов пришлось отказаться от гипотетического эфира, оставив только его физические свойства, и наделить ими само пространство. Во-вторых, именно благодаря изменению плотности физического вакуума возможны колебательные процессы в нём. И если уж говорить утилитарным языком, именно благодаря изменениям плотности пространства мы можем слушать радио и смотреть телевизор за сотни и тысячи километров от передающих антенн. В этом смысле хорошим аналогом может быть разговор двух людей, где голосовые связки одного выполняют роль антенны, воздушная среда, изменяющая свою плотность вследствие вибрации голосовых связок – роль физического вакуума, а ушные перепонки второго собеседника – роль приёмника.
Итак, о структуре пространства. За исходные пункты изложения возьмём три понятия: точка, бесконечность и движение. Точка – понятие не имеющее никакого содержания кроме протяженности бесконечно малой величины. Бесконечность также понятие не имеющее никакого содержания кроме протяженности бесконечно большой величины. Человек, появившись на свет и оказавшись между двумя этими крайностями, поневоле приносит в бесконечность свой масштаб и относительно его вынужден рассматривать понятия точки и бесконечности. Теперь точка выступает не как имеющая бесконечно малую размерность, а как масштабная точка. Масштабная точка представялет собой совокупность концентрических колец, где каждому кольцу соответствует свой относительный масштаб. При бесконечном увеличении радиуса колец масштабной точки, размерность её стремится к бесконечно большой протяженности, т. е. к реальной бесконечности. При бесконечном уменьшении радиуса колец масштабной точки, размерность её стремится к бесконечно малой величине, т. е. данной изначально точке. Уже в этих рассуждениях мы прибегли к понятию движения, когда употребляли слова «увеличение» и «уменьшение», показывая тем самым динамичный характер точки, но этим движение себя ещё не исчерпывает, ведь наше пространство трёхмерно. Движение точки даёт прямую, движение прямой – плоскость, движение плоскости – объём. Образованный движением точки, прямой и плоскости объём и будет как раз тем трёхмерным пространством, о котором идёт речь. Потому как мы говорим о нашем реальном пространстве, то примем сразу размерность полученного объёма равную бесконечности. Вместе с тем оно однородно на всём протяжении.
По структуре своей образованный объём непрерывен, но в том нет ничего нелогичного, если мы будем рассматривать его как совокупность бесконечного множества масштабных точек, и, стало быть, характеристики и свойства пространства будут определяться характеристиками и свойствами точек.
Рассмотрим один несложный опыт. Возьмём два шарика, закреплённые на концах одной пружинки. Первоначальное положение шариков будет соответствовать состоянию нулевой плотности, иначе говоря, состоянию покоя. Будем сближать шарики, нарушим состояние нулевой плотности. По мере сближения силы упругости пропорционально возрастают. Резко прекратим сближение. Шарики устремятся к своему первоначальному положению, но по инерции переходят его, создавая неустойчивое состояние деформации расширения. Возникнет колебательный процесс с определённой частотой. Через некоторое время колебания системы затухнут. Повторим опыт несколько раз, сближая шарики на различные расстояния, уменьшая его раз от раза. Во всех случаях частота колебаний оставалась прежней, а длительность их увеличивалась. Отсюда можно сделать вывод: длительность колебаний прямо пропорционально зависит от величины деформации.
Вернёмся теперь к нашему пространству и рассмотрим подобный опыт на примере двух соседних масштабных точек. Однако заметим, что между двумя соседними масштабными точками лежит такая же бесконечность, как между единицей и двойкой. Бесконечность расстояния между масштабными точками есть бесконечная последовательность масштабов. Из сказанного вытекает совершенно справедливое утверждение: две соседние точки могут бесконечно сближаться, но никогда не сблизятся. Изменение расстояния между точками есть последовательная смена масштабов: сближению точек соответствует последовательная смена крупного масштаба на более мелкий; удалению точек наоборот, смена мелкого масштаба на более крупный. Изменению расстояния между точками, в свою очередь, соответствует изменение плотности между ними: сближению точек соответствует деформация сжатия, удалению точек – деформация расширения.
Из сказанного следует: структура масштабных точек не накладывает никаких ограничений на величины изменений плотности, т. е. плотность между ними может изменяться в бесконечном диапазоне. Согласно нашему опыту с шариками, при величине деформации точек, стремящейся к бесконечности, длительность колебаний соответственно стремится к бесконечности.
Мы рассматривали две точки как бы выделенные из бесконечности пространства, не пренадлежащие ему. Теперь же обратимся к пространству в целом. Понятно, что деформация положения двух точек в какой-нибудь области приведёт к колебательному процессу этих точек, но теперь же от места колебания в бесконечность должны распространяться возбуждаемые волны. Согласитесь, если мы будем разбирать колебания и волны в непрерывной трёхмерной среде на примере двух точек, представить нам это будет довольно сложно, да и невозможно, тем более что точки мы используем только как вспомогательное средство. Уже в силу этой причины мы должны перейти к единственно возможному виду локальных колебаний в сплошых однородных средах, а именно – радиальным.
Для того чтобы легче было мысленно представить себе радиальные колебания плотности, воспользуемся чёрно-белым непрерывным спектром. Покоящемуся пространству усреднённой плотности будет соответствовать сплошной однородный фон серого цвета. Изменениям же плотности: деформации сжатия и деформации расширения соответственно потемнение и посветление серого фона.
Выделим в некоторой области нашего бесконечного объёма условную сферу. Почему сферу, а не куб или тетраэдр? Это можно объяснить, основываясь на хорошо известном нам явлении распространения сферических волн от источника в однородных средах. Теперь представим, что усреднённая плотность в окрестностях условной сферы была равномерно деформирована какими-то силами и сместилась строго радиально к центру сферы. В центре обнаружится потемнение серого фона, тогда как к периферии сферы и далее произойдёт посветление фона. Деформация плотности, когда силы прекратили своё действие, повлекла за собой колебательный процесс. Период потемнения в центре сферы сменится периодом посветления, иначе говоря, фаза сжатия сменится фазой расширения. Колебания плотности в локальной области неизбежно возбуждают сферические волны, которые, удаляясьв бесконечность, «поляризуют» всё больший и больший объём пространства. Если процесс радиальных колебаний не поддерживать, он вскоре затухнет, как и возбуждаемые волны по мере удаления. Графически процесс затухания можно изобразить нисходящей концентрической спиралью. Установится вновь состояние покоя, соответствующее усреднённой плотности, иначе, установится вновь однородный серый фон. Спроецировав условную сферу на плоскость и прибегнув к средствам мультипликации, эту картинку можно сделать динамичной и гораздо нагляднее. Вернувшись к опыту с двумя масштабными точками и опираясь на его вывод, можно сказать: если величина деформации плотности в локальной области будет эквивалентна бесконечности объёма, длительность радиальных колебаний плотности в данной области будет бесконечна.
В заключение сделаю два замечания. Первое касается характера возбуждаемых волн, второе – скорости радиальных колебаний и скорости распространения волн.
В физике известно два вида волн: продольные и поперечные. Вид волны определяется направлением вектора колебания частиц среды, в которой распространяется волна. Если вектор колебания частиц направлен вдоль распространения волны, волна называется продольной, если же поперёк распространения, то поперечной.
В нашем случае возбуждаемые волны, как и сам радиальный осциллятор, относятся к продольным волнам. Вектор колебания условных точек направлен вдоль распространения волны.
Скорость, иначе, частота радиальных колебаний плотности в локальной области есть величина постоянная, независящая от величины деформации упругой среды. Скорость же распространения возбуждаемых волн определяется скоростью радиальных колебаний и является вполне определённой и неизменной. Прибегая к аналогии со звуковыми волнами, заметим, что их скорость распространения не изменится от того, насколько сильно голосовые связки деформируют воздушную среду.
Можно надеяться, что изложенная здесь модель процессов радиальных колебаний плотности в упругой среде, скоро найдёт себе применение в физике, и с успехом.
detector