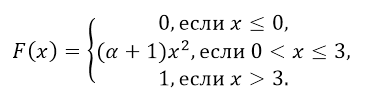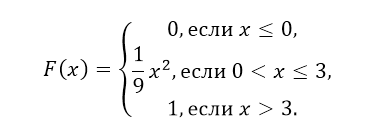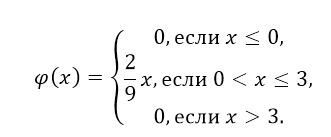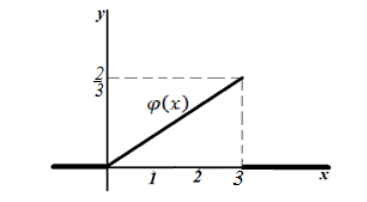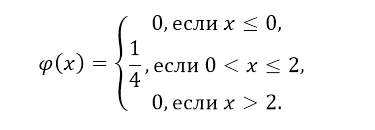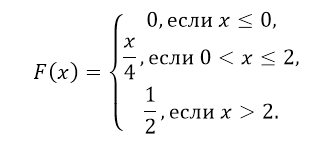Как вычислить плотность распределения зная функцию распределения

Формулы онлайн: Случайные величины

В данном разделе вы найдете формулы по теории вероятностей в онлайн-варианте (в формате для скачивания — см. на странице Таблицы и формулы по теории вероятностей).

Каталог формул по теории вероятности онлайн

Случайные величины. Способы задания

Ряд распределения дискретной случайной величины

$$ \begin <|c|c|>\hline X_i & x_1 & x_2 & \dots & x_n \\ \hline p_i & p_1 & p_2 & \dots & p_n \\ \hline \end $$

Сумма вероятностей всегда равна 1 (условие нормировки):

Функция распределения (интегральная функция распределения)

Функция распределения случайной величины $X$ определяется по формуле $F(x)=P(X\lt x)$. Это неубывающая функция, принимающая значения от 0 до 1. Если задана плотность распределения $f(x)$, то функция распределения выражается как интеграл от плотности:

Плотность распределения (дифференциальная функция распределения)

Плотность распределения случайной величины $X$ определяется по формуле $f(x)=F'(x)$. Существует только для непрерывной случайной величины. Для нее выполняется условие нормировки (площадь под кривой вероятности равна 1):

Вероятность попадания случайной величины в заданный интервал

Может быть вычислена двумя способами:

1) через функцию распределения

$$P(\alpha \lt X \lt \beta) = F(\beta)-F(\alpha).$$

2) через плотность распределения

Случайные величины. Числовые характеристики

Математическое ожидание случайной величины

1) Для дискретной случайной величины $X$, заданной рядом распределения:

2) Для непрерывной случайной величины $X$, заданной плотностью распределения:

Дисперсия случайной величины

По определению дисперсия – это второй центральный момент:

$$ D(X) =M\left[ \left(X-M(X)\right)^2 \right] =M(X^2)-\left(M(X)\right)^2.$$

1) Для дискретной случайной величины $X$:

$$ D(X)= \sum_^ x_i^2 \cdot p_i — \left(M(X)\right)^2.$$

2) Для непрерывной случайной величины $X$:

Среднее квадратическое отклонение случайной величины

Коэффициент вариации случайной величины

Начальный момент r–го порядка случайной величины

В частности, первый начальный момент – это математическое ожидание: $\nu_1=M(X^1)=M(X).$

Центральный момент r – го порядка случайной величины

$$\mu_r = M\left[ \left(X-M(X)\right)^r \right]$$

В частности, второй центральный момент – это дисперсия:

$$\mu_2 = M\left[ \left(X-M(X)\right)^2 \right] = D(X).$$

Асимметрия

Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого (правая часть кривой более пологая), и отрицателен в противном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.

Эксцесс

Коэффициент эксцесса нормального распределения равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик гладкий.

Решенные задачи по теории вероятностей

Нужна готовая задача по терверу? Найдите на сайте-решебнике:

Источник

Функция плотности распределения

Пусть имеется непрерывная случайная величина X с функцией распределения F (х), которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от

т. е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка,- т. е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать к нулю.

В пределе получим производную от функции распределения:

• Функция f (х) — производная функции распределения — характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке.

Эта функция называется плотностъю распределения (иначе «плотностью вероятности») непрерывной случайной величины X. Иногда функцию f (х) называют также «дифференциальной функцией распределения» или «диффе-ренциальным законом распределения величины X.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Термины «плотность распределения», «плотность вероятности»

Термины «плотность распределения», «плотность вероятности» становятся особенно наглядными Рис. 5.4.1. при пользовании механической интерпретацией распределения; в этой интерпретации функция f (х) буквально характеризует плотность распределения масс по оси абсцисс (так называемую «линейную плотность»).

Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 5.4.1).

Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.

Рассмотрим непрерывную случайную величину X с плотностью распределения и элементарный участок dx, примыкающий к точке х (рис. 5.4.2). Вероят ность попадания случайной величины X

на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна f(x)dx. Величина f(x)dx называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок dx (рис. 5.4.2).

Возможно вам будут полезны данные страницы:

Выразим вероятность попадания величины X на отрезок от а до 0 (рис. 5.4.3) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т. е. интегралу:

Геометрически вероятность попадания величины X на участок равна площади кривой распределения, опирающсйся на этот участок (рис. 5.4.3).

Формула (5.4.2) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению

откуда по формуле (5.4.3) имеем:

Геометрически F (х) есть не что иное, как площадь кривой распределения, лежащая левее точки х (рис. 5.4.4).

Укажем основные свойства плотности распределения:

1. Плотность распределения есть неотрицательная функция: Это свойство непосредственно вытекает из того, что функция распределения F (х) есть неубывающая функция.

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

Это следует из формулы (5.4.4) и из того, что геометрически основные свойства плотности распределения означают, что:

1. вся Кривая распределения лежит не ниже оси абсцисс;
2. полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Выясним размерности основных характеристик случайной величины — функции распределения и плотности распределения. Функция распределения F (х), как всякая вероятность, есть величина безразмерная. Размерность плотности распределения /(х), как видно из Формулы (5.4.1), обратна размерности случайной величины.

Примеры с решением

Пример 1. Функция распределения непрерывной случайной величины X задана выоажением

а) Найти коэффициент а.

б) Найти плотность распределения f (х).

в) Найти вероятность попадания величины X на участок от 0,25 до 0,5.

а) Так как функция распределения величины X непрерывна, то при

б) Плотность распределения величины X выражается формулой

в) По формуле (5.3.1) имеем:

Пример 2. Случайная величина X подчинена закону распределения с плотностью:

а) Найти коэффициент а,

б) Построить график плотности распределения /(х).

в) Найти функцию распределения F (х) и построить ее график,

г) Найти вероятность попадания величины X на участок от

а) Для определения коэффициента а воспользуемся свойством плотности распределения:

б) График плотности f (х) представлен на рис. 5.4.5.

в) По формуле (5.4.4) получаем выражение функции распределения:

График функции F (х) изображен на рис. 5.4.6.

Тот же результат, но несколько более сложным путем можно получить по формуле (.5.4.3).

Пример 3. Плотность распределения случайной величины X задана формулой:

а) Построить график плотности

б) Найти вероятность того, что величина X попадет на участок (—1,+1).

а) График плотности дан на рис. 5.4.7.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник

Определение плотности распределения

Вы будете перенаправлены на Автор24

Как нам уже известно, случайную величину можно задавать с помощью таблицы или с помощью функции распределения вероятности. Предположим теперь, что случайная величина $X$ является непрерывной, а функция распределения вероятности $F(x)$ непрерывна и дифференцируема в своей области определения. Тогда для такой случайной величины существует еще один способ её задания — задания с помощью плотности распределения.

Плотностью распределения $\varphi (x)$ непрерыной случайной величины называется первая производная от функции распределения вероятности $F(x)$.

. Подчеркнем, что данное понятие не применимо к дискретной случайной величине.

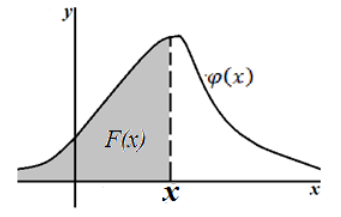
Геометрически, плотность распределения связана с функцией распределения вероятностей следующим образом: площадь криволинейной трапеции, ограниченной графиком плотности распределения и находящейся по левую сторону от величины $x$ и есть функция распределения вероятности (рис. 1).

Рисунок 1. Связь функций $\varphi (x)$ и $F(x)$.

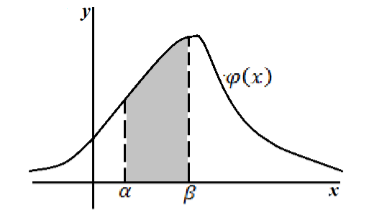
Геометрический смысл: вероятность попадания непрерывной случайной величины в интервал $(\alpha ,\beta )$ равна площади криволинейной трапеции, ограниченной графиком функции распределения $\varphi \left(x\right)$ и прямыми $x=\alpha ,$ $x=\beta $ и $y=0$ (рис. 2).

Рисунок 2. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(\alpha ,\beta )$.

Готовые работы на аналогичную тему

Примеры задач на понятие плотности распределения

Пусть функция распределения $F(x)$ случайной величины $X$ имеет следующий вид:

б) Найти плотность распределения $\varphi \left(x\right)$.

в) Построить график плотности распределения.

а) Так как необходимо найти плотность распределения, то случайная величина $X$ является непрерывной.

Тогда, при $x=3$, получим, что $(\alpha +1)x^2=1$, то есть

б) Так как $\varphi (x)$ = $F'(x)$, то получим:

в) Построим график функции $\varphi \left(x\right)$.

г) Воспользовавшись геометрическим смыслом функции плотности распределения получим, что нам нужно найти площадь криволинейной трапеции, ограниченной функцией $y=\frac<2><9>x$ и прямыми $x=1,$ $x=2$ и $y=0$.

Найти функцию распределения непрерывной случайной величины и построить её график, если плотность распределения имеет вид:

При решении будем использовать следующую формулу: $F\left(x\right)=\int\limits^x_<-\infty ><\varphi (x)dx>$

\begin \item При $x\le 0$, по формуле, получим:

\item При $x>2$, по формуле, получим:

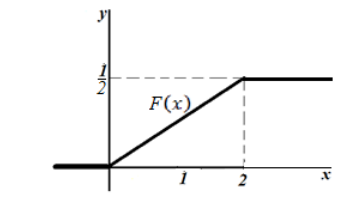
Таким образом, функция распределения имеет вид:

. Заметим, что, так как дана плотность распределения, то случайная величина является непрерывной. Следовательно, функция $F(x)$ также должна быть непрерывной (как и получилось в нашем примере). Это может служить косвенной проверкой правильности решения такого рода задач.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 20 02 2022

Источник