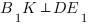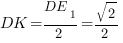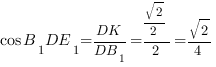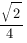Как найти угол между непересекающимися прямыми в кубе

Угол между скрещивающимися прямыми – определение, примеры нахождения.

В этой статье сначала дадим определение угла между скрещивающимися прямыми и приведем графическую иллюстрацию. Далее ответим на вопрос: «Как найти угол между скрещивающимися прямыми, если известны координаты направляющих векторов этих прямых в прямоугольной системе координат»? В заключении попрактикуемся в нахождении угла между скрещивающимися прямыми при решении примеров и задач.

Угол между скрещивающимися прямыми — определение.

К определению угла между скрещивающимися прямыми будем подходить постепенно.

Сначала напомним определение скрещивающихся прямых: две прямые в трехмерном пространстве называются скрещивающимися, если они не лежат в одной плоскости. Из этого определения следует, что скрещивающиеся прямые не пересекаются, не параллельны, и, тем более, не совпадают, иначе они обе лежали бы в некоторой плоскости.

Приведем еще вспомогательные рассуждения.

Пусть в трехмерном пространстве заданы две скрещивающиеся прямые a и b . Построим прямые a₁ и b₁ так, чтобы они были параллельны скрещивающимся прямым a и b соответственно и проходили через некоторую точку пространства M₁ . Таким образом, мы получим две пересекающиеся прямые a₁ и b₁ . Пусть угол между пересекающимися прямыми a₁ и b₁ равен углу . Теперь построим прямые a₂ и b₂ , параллельные скрещивающимся прямым a и b соответственно, проходящие через точку М₂ , отличную от точки М₁ . Угол между пересекающимися прямыми a₂ и b₂ также будет равен углу . Это утверждение справедливо, так как прямые a₁ и b₁ совпадут с прямыми a₂ и b₂ соответственно, если выполнить параллельный перенос, при котором точка М₁ перейдет в точку М₂ . Таким образом, мера угла между двумя пересекающимися в точке М прямыми, соответственно параллельными заданным скрещивающимся прямым, не зависит от выбора точки М .

Теперь мы готовы к тому, чтобы дать определение угла между скрещивающимися прямыми.

Угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым.

Из определения следует, что угол между скрещивающимися прямыми также не будет зависеть от выбора точки M . Поэтому в качестве точки М можно взять любую точку, принадлежащую одной из скрещивающихся прямых.

Приведем иллюстрацию определения угла между скрещивающимися прямыми.

Нахождение угла между скрещивающимися прямыми.

Так как угол между скрещивающимися прямыми определяется через угол между пересекающимися прямым, то нахождение угла между скрещивающимися прямыми сводится к нахождению угла между соответствующими пересекающимися прямыми в трехмерном пространстве.

Несомненно, для нахождения угла между скрещивающимися прямыми подходят методы, изучаемые на уроках геометрии в средней школе. То есть, выполнив необходимые построения, можно связать искомый угол с каким-либо известным из условия углом, основываясь на равенстве или подобии фигур, в некоторых случаях поможет теорема косинусов , а иногда к результату приводит определение синуса, косинуса и тангенса угла прямоугольного треугольника.

Однако очень удобно решать задачу нахождения угла между скрещивающимися прямыми методом координат. Именно его и рассмотрим.

Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz (правда, во многих задачах ее приходится вводить самостоятельно).

Поставим перед собой задачу: найти угол между скрещивающимися прямыми a и b , которым соответствуют в прямоугольной системе координат Oxyz некоторые уравнения прямой в пространстве.

Возьмем произвольную точку трехмерного пространства М и будем считать, что через нее проходят прямые a₁ и b₁ , параллельные скрещивающимся прямым a и b соответственно. Тогда искомый угол между скрещивающимися прямыми a и b равен углу между пересекающимися прямыми a₁ и b₁ по определению.

Таким образом, нам осталось найти угол между пересекающимися прямыми a₁ и b₁ . Чтобы применить формулу для нахождения угла между двумя пересекающимися прямыми в пространстве нам нужно знать координаты направляющих векторов прямых a₁ и b₁ .

Как же мы их можем получить? А очень просто. Определение направляющего вектора прямой позволяет утверждать, что множества направляющих векторов параллельных прямых совпадают. Следовательно, в качестве направляющих векторов прямых a₁ и b₁ можно принять направляющие векторы и прямых a и b соответственно.

Координаты векторов и определяются либо по известным из условия уравнениям прямых a и b (смотрите раздел координаты направляющего вектора прямой), либо по известным из условия координатам двух точек прямых a и b (здесь может быть полезна теория раздела координаты вектора через координаты точек его начала и конца).

Итак, угол между двумя скрещивающимися прямыми a и b вычисляется по формуле , где и — направляющие векторы прямых a и b соответственно.

Формула для нахождения косинуса угла между скрещивающимися прямыми a и b имеет вид .

Основное тригонометрическое тождество позволяет найти синус угла между скрещивающимися прямыми, если известен косинус: .

Осталось разобрать решения примеров.

Найдите угол между скрещивающимися прямыми a и b , которые определены в прямоугольной системе координат Oxyz уравнениями и .

Канонические уравнения прямой в пространстве позволяют сразу определить координаты направляющего вектор этой прямой – их дают числа в знаменателях дробей, то есть, — направляющий вектор прямой . Параметрические уравнения прямой в пространстве также дают возможность сразу записать координаты направляющего вектора – они равны коэффициентам перед параметром, то есть, — направляющий вектор прямой . Таким образом, мы располагаем всеми необходимыми данными для применения формулы, по которой вычисляется угол между скрещивающимися прямыми:

угол между заданными скрещивающимися прямыми равен .

Найдите синус и косинус угла между скрещивающимися прямыми, на которых лежат ребра AD и BC пирамиды АВСD , если известны координаты ее вершин: .

Направляющими векторами скрещивающихся прямых AD и BC являются векторы и . Вычислим их координаты как разность соответствующих координат точек конца и начала вектора:

По формуле мы можем вычислить косинус угла между указанными скрещивающимися прямыми:

Теперь вычислим синус угла между скрещивающимися прямыми:

В заключении рассмотрим решение задачи, в которой требуется отыскать угол между скрещивающимися прямыми, а прямоугольную систему координат приходится вводить самостоятельно.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁ , у которого АВ=3 , АD=2 и AA₁=7 единиц. Точка E лежит на ребре АА₁ и делит его в отношении 5 к 2 считая от точки А . Найдите угол между скрещивающимися прямыми ВЕ и А₁С .

Так как ребра прямоугольного параллелепипеда при одной вершине взаимно перпендикулярны, то удобно ввести прямоугольную систему координат, и определить угол между указанными скрещивающимися прямыми методом координат через угол между направляющими векторами этих прямых.

Введем прямоугольную систему координат Oxyz следующим образом: пусть начало координат совпадает с вершиной А , ось Ox совпадает с прямой АD , ось Oy — с прямой АВ , а ось Oz – с прямой АА₁ .

Тогда точка В имеет координаты , точка Е — (при необходимости смотрите статью деление отрезка в данном отношении), точка А₁ — , а точка С — . По координатам этих точек мы можем вычислить координаты векторов и . Имеем , .

Осталось применить формулу для нахождения угла между скрещивающимися прямыми по координатам направляющих векторов:

Источник

10 класс. Геометрия. Скрещивающиеся прямые.

10 класс. Геометрия. Скрещивающиеся прямые.

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Скрещивающиеся прямые. Примеры решения задач.

При решении задач на нахождение угла между скрещивающимися прямыми удобно пользоваться таким алгоритмом:

1. Провести прямую, параллельную одной из двух скрещивающихся прямых так, чтобы она пересекала вторую прямую. Мы получим пересекающиеся прямые, угол между которыми равен углу между исходными скрещивающимися.

2. Найти треугольник, в котором этот угол будет внутренним углом.

3. С помощью данных задачи найти тригонометрическую функцию этого внутреннего угол или сам угол.

Рассмотрим этот алгоритм подробнее на примере решения задач.

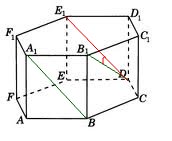
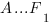
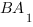
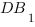
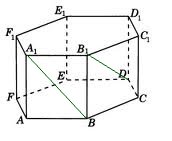
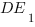
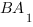
1. В правильной шестиугольной призме , все ребра которой равны 1, найти косинус угла между прямыми и :

Проведем прямую параллельно прямой :

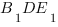
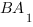
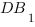
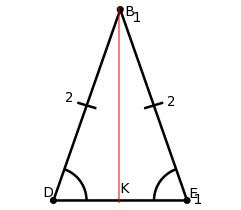
Угол равен углу между прямыми и , так как эти углы имеют параллельные стороны.

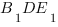
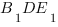
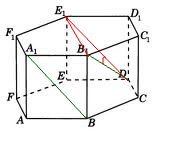
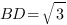
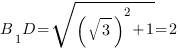
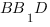
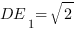
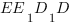
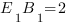
Чтобы найти косинус угла , рассмотрим треугольник :

Найдем длины сторон этого треугольника. Для этого вспомним, чему равны элементыправильного шестугольника все стороны которого равны 1.

, (из треугольника )

(как диагональ квадрата )

— диаметр окружности, описанной около правильного шестиугольника со сторонами, равными 1.

Мы получили равнобедренный треугольник :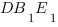

Ответ:

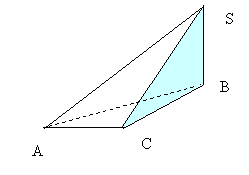
Задача 2. В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине С, гипотенузой AB равной 13 и катетом AC, равным 12. Вершина S пирамиды проектируется в точку B основания. Боковое ребро CS равно 5. Найдите расстояние между ребрами AS и BC.

Нам нужно найти расстояние между двумя отрезками AS и BC. Эти отрезки лежат на скрещивающихся прямых. Действительно из условия следует, что точка SABC, а AABC, следовательно, прямая, AS пересекает плоскость ABC и так как BCABC и ABC, то наше утверждение следует из признака скрещивающихся прямых. Теперь мы можем сформулировать задачу точнее: нам нужно найти расстояние между скрещивающимися прямыми.

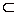
Определение 1. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.(Геометрия 10-11 кл. Л. С. Атанасян и др. М. Просвещенние, 2009 г.)

Следуя этому определению нам необходимо построить плоскость, проходящую через одну из скрещивающих прямых, параллельно другой и построить перпендикуляр к этой плоскости из точки принадлежащей другой прямой.

Какую прямую выбрать? Обычно такая задача решается перебором.

Мы выбрали прямую AS, проведем через эту прямую плоскость параллельную BC. Для наглядности выполним следующие далеко не очевидные построения.

1. Достроим пирамиду до параллелепипеда. Для этого через точку А в плоскости ABC проведем прямую параллельную прямой ВС и через точку В прямую параллельную прямой АС, точку пепесечения построенных прямых обозначим буквой D. Через точки A, C, D проведем прямые параллельные прямой SB, на каждой из них отложим отрезки равные отрезку BS, и полученные точки соединим отрезками.

2. Далее построим сечение параллелепипеда ABCDA1B1C1D1 плоскостью ADS, в сечением будет параллелограмм ADSC1 (ребра параллелепипеда AD и C1S равны и параллельны>

3. Плоскости ADS и ADSC1 совпадают или, если хотите, это одна и таже плоскость. Предположим, что это разные не совпадающие плоскости. Тогда по условию эти плоскости имеют три общие точки A, D и S. Но тогда согласно аксиоме «Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей» точки A, D и S лежат на одной прямой, тогда SАD, так как АDАВС, то SАВС, но это противоречит условию. Значит наше предположение не верно. Тогда плоскости ADS и ADSC1совпадают.

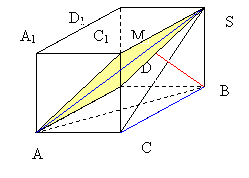
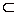
4. Пусть прямая BM перпендикулярна прямой DS. Отрезок BM есть кратчайшее расстояние между скрещивающимися прямыми. Докажем это утверждение. Из условия следует, что BC BS и BCAC, так как AC||DB, то BCDB, так как к тому же BD и BS пересекающиеся прямые, то BCDBS, но тогда и ADDBS, посколько BMDBS, то BMAD. Так как BM перпендикулярна к двум пересекающимся прямым AD и DS лежащим в плоскости ADSC1, то BMADSC1.

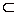
5. Для того чтобы вычислить длину отрезка BM нам необходимо вычислить длины отрезков BC, BS и DS.

По условию C прямой, поэтому ABC — прямоугольный, следовательно, AB2= AC2 + BC2;

По условию S проектируется в B, поэтому BSABC, BCABC, следовательно BSBC. значит CSB — прямоугольный, следовательно, CS2 = BC2 + BS2;

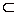
BS2 = (5)2 — 52;

BSABC, по построению BDABC, поэтому BSBD откуда следует, что BDM — прямоугольный, следовательно, DM2 = DB2 — BM 2;

BMS прямоугольный, следовательно, MS2 = BS2 — BM2

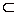
DM = ;

MS = ;

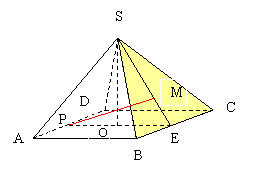
Так как BM общий катет двух прямоугольных треугольников с гипотенузами 10 и 12, то 0 0, 122 — x2 > 0 .

Составить уравнение можно двумя способами либо использовать очевидное равенство DS = DM + MS, либо исплльзовать свойство перпендикуляра проведенного из вершины прямого угла к гипотенузе. И в том и другом случае получим иррациональное уравнение. Эти уравнения имеют разную сложность. Пойдем по второму пути, так как , по нашему мнению, уравнение будеть более простым.

BM2 = DMMS;

x2 = ; возведем обе части уравнения в квадрат, учитывая выше изложенные рассуждения, получим уравнение равносильное данному.

x4 = 14400 — 100×2 — 144×2 + x4;

x = .

Растояние между ребрами AS и BC равно .

Решить эту задачу можно и иначе. В учебнике Геометрия 7-11кл. А. В. Погорелов М. Просвещение 2009г. понятие расстояние между скрещивающими прямыми определяется так.

Определение 2. Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.

Чтобы построить общий перпендикуляр скрещивающих прямых выполним следующие построения. Чтобы не повторятся строить параллелепипед мы не будем и рисунок будет проще.

Через точку А в плоскости АВС проведем AD||BC и через точку В проведем BD||AC. В плоскости SDB из точки В проведем BMDS и через точку М проведем QM||AD. Через точку Q проведем QP||MB. Отрезок QP — это общий перпендикуляр скрещивающихся прямых AS и BC.

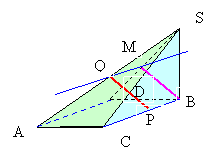
Выше мы доказали, что BMADS. Так как по построениюQP||BM, то QPADS. ADADS поэтому QPAD.

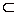
С другой стороны BC перпендикулярна двум пересекающимся прямым BS и BD, следовательно, BM BC, но тогда так как MB||QP, то QPBC.

QMBP — параллелограмм, следовательно, QP = BM. Как вычисляется длина отрезка BM. мы рассотрели выше.

Задача 3. В основании пирамиды SABCD лежит прямоугольник.
BC = a, DC = b.
Основание высоты пирамиды совпадает с центром симметрии ABCD.
Боковое ребро пирамиды равно c.
Найти растояние между ребрами AD и SC.

Ребра AD и SC лежат на скрещивающихся прямых. Прямая AD параллельна плоскости SBC, проходящей через прямую SC. Проведем в этой плоскости SEBC. и через точку E проведем прямую ОE, где О основание высоты пирамиды. Точку пересения прямых ОЕ и AD обозначим Р. В плоскости SPE проведем PMSE. Отрезок PM это кратчайшее расстояние между скрещивающими прямыми AD и SC. Докажем это утверждение. По построению ОЕ проекция наклонной SE через основание, которой проведена прямая ВС. Из теоремы о трех перпендикулярах следует, что PЕВС. Прямые SE и PE лежат в плоскости SEP и S пересекающиеся, следовательно, BCSEP откуда следует, РМВС. Таким образом РМ перпендикулярна двум пересекающимся прямым SE и BC лежащим в плоскости SВС, значит по признаку перпендикулярности прямой к плоскости РМ SВС и согласно определению 1 является растоянием между скрещивающимися прямыии AD и SC.

Теперь вычислим PM. По условию основание высоты пирамиды совпадает с центром симметрии прямоугольника, поэтому O середина диагоналей AC и BD, тогда, во первых OPE, во вторых боковые ребра SA = SB = SC = SD. Из равенства боковых ребер пирамиды следует, что SBC равнобедренный треугольник и поэтому его высота SE является медианой и поэтому EC = 0,5a и SE2= c2 — 0,25a2.

Из прямоугольного треугольника SOE следует, что SO2 = SE2 — OE2 ,

Из этого же треугольника и определения синуса для острого угла следует, что

sinSEO=.

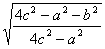
Из прямоугольного треугольника PME и определения синуса для острого угла следует, что PM = PEsinSEO, тогда

PM=b.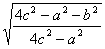

Обратите внимание на то, что искомый отрезок находится в плоскости перпендикулярной к одной из скрещивающихся прямых. Этот факт позволяет нам предложить следущий способ решения задач на нахождение расстояния между скрещивающимися прямыми.

1. Строим плоскость перпендикулярную к одной из скрещивающихся прямых. В задаче 1 это плоскость DD1SC.

2. Проецируем каждую из скрещивающихся прямых на эту плоскость. Проекцией одной из них будет точка. В задаче 1 проекция прямой ВС будет точка С, а проекция прямой AS будет прямая SD. Таким образом да И данную задачу формулируем так: «найти расстояние от точки до прямой. В задаче 1 найти расстояние от точки С до прямой DS.

3. Проводим перпендикуляр от точки до прямой. Это будет всегда перпендикуляр, проведенный из вершины прямого угла прямоугольного треугольника к гипотенузе и, следовательно, всегда можно применить его свойство, для чего прдварительно находим гипотенузу и катеты прямоугольного треугольника..

Для закрепления навыка нахождения расстояния между скрещивающимися проямыми предлагаем решить следующие задачи. Постройте изображение куба и найдите пары скрещивающиеся прямых. Для каждой выбранной пары прямых докажите, используя признак скрещивающихся прямых, что это скрещивающиеся прямые.

Замечание. В том случае, когда возникают затруднения в нахождении пар скрещивающихся прямых можно самостоятельно изготовить из бумаги или из спичек и пластелина модель куба и на этой модели выполнять поиск прямых. Желательно модель размещать в различных положениях. После работы с моделью проделайте эту работу мысленно, пытаясь в воображении представить модель куба и лишь потом перейти к рисунку.

Задача 4. 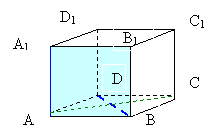Дан куб ABCDA1B1C1D1.
AB = 5 см.
Найти расстояние между прямыми AA1 и BD.
Подсказка. Обратите внимание на отрезок АC

Источник