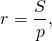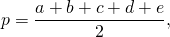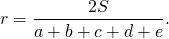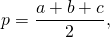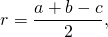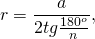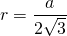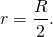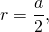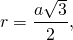Как найти радиус окружности вписанной в куб

Радиус вписанной сферы куба

Свойства

Радиус вписанной сферы куба представляет собой половину ребра куба, так как диаметр такой сферы точно совпадает с самим ребром. Поэтому чтобы найти ребро куба через радиус вписанной сферы, нужно умножить последний на два. (рис.2.2) a=2r

Найти площадь стороны куба можно как площадь квадрата, стороной которого является ребро куба. Тогда, вместо того чтобы возводить во вторую степень ребро, нужно возвести удвоенный радиус вписанной в куб сферы. Площадь боковой поверхности куба и площадь полной поверхности куба будут равны четырем и шести таким площадям соответственно, так как они представлены эти количеством граней куба. S=a^2=4r^2 S_(б.п.)=4S=16r^2 S_(п.п.)=6S=24r^2

Чтобы вычислить объем, необходимо возвести в куб ребро a или удвоенный радиус вписанной сферы. Таким образом, мы получим, что объем куба через радиус сферы, вписанной в него, равен кубу этого радиуса, умноженному на 8. V=a^3=8r^3

Периметр куба, как сумма длин всех ребер по одной стороне, равен произведению длины одного ребра и двенадцать. Периметр, выраженный через радиус вписанной окружности, равен 24 таким радиусам. P=12a=24r

Диагональ стороны куба, то есть диагональ квадрата, вычисляется как произведение ребра куба на корень из двух, в данном случае она будет выглядеть как произведение радиуса вписанной сферы на 2 корня из двух. d=a√2=2√2 r

Чтобы найти диагональ куба через радиус вписанной сферы, воспользуемся готовой формулой для диагонали куба через ребро и подставим вместо него удвоенный радиус. (рис.2.1.) D=a√3=2√3 r

Радиус окружности, описанной вокруг куба, равен половине диагонали, как видно из рисунка. Так как диагональ куба равна удвоенному произведению радиуса и корня из трех, то разделив это выражение на два, коэффициенты сократятся, и останется только радиус, умноженный на корень из трех. (рис.2.3.) R=D/2=(2√3 r)/2=√3 r

Источник

Чему равен радиус вписанной окружности

Вписанная окружность — в какую фигуру нельзя вписать

Для решения геометрических задач можно использовать различные формулы и приемы, которые помогут облегчить поиск искомых показателей. Один из способов найти различные неизвестные в многогранной фигуре – сделать это через вписанную окружность.

Вписанная окружность — окружность, которая лежит внутри угла и касается его сторон. Касание происходит в одной точке с каждой стороны.

Вписанная в фигуру окружность, например, в треугольник или многоугольник, будет касаться всех его сторон. Это главное свойство окружности, которая будет называться вписанной. Сама фигура в таком случае называется описанной вокруг окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Из этого следует, что вписанная окружность не будет таковой, если не будет касаться всех сторон фигуры.

Окружность точно можно вписать в следующие геометрические фигуры:

• треугольник;
• выпуклый правильный многоугольник;
• квадрат;
• равнобедренная трапеция;
• ромб.

При этом окружность в данные фигуры может быть вписана лишь единожды.

Четырехугольник является неоднозначной фигурой при процессе вписывания в нее окружности. Для того, чтобы окружность была вписанной в четырехугольник, суммы длин его противоположных сторон должны быть равны.

Окружность точно нельзя вписать в следующие геометрические фигуры:

• прямоугольник;
• параллелограмм (если он не является ромбом).

Ни один из видов данных фигур не сможет иметь вписанную окружность, так как она не сможет соприкасаться со всеми их сторонами, что является главным признаком вписанной окружности.

Теорема о вписанной окружности

Теорема о вписанной окружности гласит, что в любой треугольник и в любой выпуклый многоугольник и четырехугольник с равными суммами длин противоположных сторон можно вписать окружность, но только одну.

Правило о центре вписанной окружности

Центр окружности при этом будет находиться в точке пересечения биссектрис фигуры. Чтобы определить центр, нужно построить биссектрисы из каждого угла и найти пересечение.

Формула нахождения радиуса вписанной окружности

Вычисление радиуса вписанной окружности ведется по формулам, которые зависят от фигуры и известных данных. Главным условием является тот факт, что фигура должна подходить под список тех, в которые можно вписать окружность.

Радиус — перпендикуляр, соединяющий центр окружности с любой точкой, лежащей на окружности. По длине радиус составляет половину диаметра.

Треугольник

Формула нахождения радиуса окружности, вписанной в треугольник через все стороны:

a, b и c — стороны треугольника,

Формула нахождения радиуса окружности, вписанной в треугольник через сторону и высоту:

a и b — стороны треугольника,

Равносторонний треугольник

Формула нахождения радиуса окружности, вписанной в равносторонний треугольник:

Равнобедренный треугольник

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через значения сторон:

a и b — стороны треугольника.

Формула нахождения радиуса окружности, вписанной в равнобедренный треугольник через сторону и угол:

A и b — стороны треугольника,

Прямоугольный треугольник

Формула нахождения радиуса окружности, вписанной в прямоугольный треугольник:

a и b — катеты треугольника,

Равнобедренная трапеция

Формула нахождения радиуса окружности, вписанной в равнобедренную трапецию:

Квадрат

Формула нахождения радиуса окружности, вписанной в квадрат:

Формула нахождения радиуса окружности, вписанной в ромб через значения диагоналей:

Формула нахождения радиуса окружности, вписанной в ромб через значения стороны и угла:

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и угол:

Формула нахождения радиуса окружности, вписанной в ромб через диагональ и сторону:

Формула нахождения радиуса окружности, вписанной в ромб через высоту:

а — сторона ромба,

Многоугольник

Формула нахождения радиуса окружности, вписанной в правильный многоугольник:

N — количество сторон многоугольника.

Шестиугольник

Формула нахождения радиуса окружности, вписанной в шестиугольник:

Источник

Как найти радиус окружности вписанной в куб

В куб с ребром 21 вписан шар. Найдите объем этого шара, деленный на

Радиус вписанного в куб шара равен половине длины ребра куба: Тогда объем шара

Аналоги к заданию № 27126: 75315 75317 75319 Все

В прямоугольный параллелепипед вписана сфера с радиусом 4. Найдите объём параллелепипеда.

Поскольку сфера вписана в прямоугольный параллелепипед, прямоугольный параллелепипед — это куб, ребро которого равно двум радиусам вписанной сферы. Объём куба равен кубу его ребра. Следовательно,

В прямоугольный параллелепипед вписана сфера с радиусом 5. Найдите объём параллелепипеда.

Поскольку сфера вписана в прямоугольный параллелепипед, прямоугольный параллелепипед — это куб, ребро которого равно двум радиусам вписанной сферы. Объём куба равен кубу его ребра. Следовательно,

Аналоги к заданию № 525402: 525447 Все

Шар, объём которого равен 6π, вписан в куб. Найдите объём куба.

Ребро куба равно двум радиусам вписанного в куб шара, поэтому объем куба, выраженный через радиус вписанного в него шара, даётся формулой Объём шара вычисляется по формуле откуда имеем:

Тем самым, объём куба равен 36.

Шар, объём которого равен вписан в куб. Найдите объём куба.

Ребро куба равно двум радиусам вписанного в куб шара, поэтому объем куба, выраженный через радиус вписанного в него шара, даётся формулой Объём шара вычисляется по формуле откуда имеем:

Тем самым, объём куба равен 210.

Шар, объём которого равен 28π, вписан в куб. Найдите объём куба.

Ребро куба равно двум радиусам вписанного в куб шара, поэтому объем куба, выраженный через радиус вписанного в него шара, даётся формулой Объём шара вычисляется по формуле откуда имеем:

Тем самым, объём куба равен 168.

Шар, объём которого равен 44π, вписан в куб. Найдите объём куба.

Ребро куба равно двум радиусам вписанного в куб шара, поэтому объем куба, выраженный через радиус вписанного в него шара, даётся формулой Объём шара вычисляется по формуле откуда имеем:

Тем самым, объём куба равен 264.

Известно, что AB, AC, AD, DE, DF — рёбра куба. Через вершины E, F и середины рёбер AB и AC проведена плоскость P, делящая шар, вписанный в куб, на две части.

б) Найдите отношение объёма меньшей части шара к объёму всего шара.

а) Проведем TK, KF и ET и получим искомое сечение — равнобедренную трапецию FKTE.

б) Введем обозначения, как показано на рисунке. Пусть точка O — середина высоты куба и центр вписанного шара, точки O₁ и O₂ — центры нижней и верхней граней куба соответсвенно, а также точки касания шара с гранями. Пусть R — радиус шара. Очевидно, что сечением шара плоскостью P является круг, центр которого лежит на NO₂, где N — середина TK. Более того, центром данного круга является точка H — основание перпендикуляра из O на NO₂, а радиусом — HO₂. Наша задача сводится к нахождению объема шарового сегмента. Основание шарового сегмента есть круг с центром H и радиусом HO₂, высотой сегмента является отрезок, равный Найдем значения этих элементов.

Тогда по формуле объема шарового сегмента находим

Следовательно, отношение объемов равно

Ответ:

Источник: А. Ларин: Тренировочный вариант № 87.

Источник

Нахождение радиуса вписанного в куб шара

В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.

Примечание: Напомним, что в любой куб можно вписать шар.

Для начала выполним чертеж.

• шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
• центр шара – точка O, которая также является центром куба.

Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:

R = a/2, где “a” – ребро куба (является стороной его грани).

Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.

Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.

Радиус вписанного шара через диагональ куба

Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:

Источник

Радиус вписанной окружности

Удобно, когда все формулы, по которым можно найти радиус вписанной в треугольник и в многоугольник окружности, размещены на одной странице.

Радиус вписанной в многоугольник окружности

Если в многоугольник можно вписать окружность, то формула для вычисления радиуса вписанной окружности:

где p — полупериметр, то есть полусумма длин всех сторон этого многоугольника.

Например, для пятиугольника со сторонами a, b, c, d, e радиус вписанной окружности находится по формуле

Радиус вписанной в треугольник окружности

Формула для нахождения радиуса вписанной в треугольник окружности (верна для треугольника любого вида)

где a, b, c — стороны треугольника.

Радиус вписанной в прямоугольный треугольник окружности

Формула для нахождения радиуса окружности, вписанной в прямоугольный треугольник

где a и b — катеты, c — гипотенуза.

Радиус окружности, вписанной в правильный многоугольник

Формула радиуса вписанной в правильный многоугольник окружности

где a — сторона многоугольника, n — количество сторон.

Частные случаи — правильный (равносторонний) треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник.

Радиус окружности, вписанной в правильный треугольник

Формула радиуса вписанной окружности для правильного треугольника:

В правильном треугольнике радиус вписанной окружности вдвое меньше радиуса описанной окружности:

Радиус окружности, вписанной в квадрат

Формула радиуса вписанной в квадрат окружности:

Радиус окружности, вписанной в правильный шестиугольник

Формула радиуса вписанной в правильный шестиугольник окружности:

где a — сторона правильного шестиугольника.

Для любого многоугольника центр вписанной окружности лежит в точке пересечения его биссектрис.

5 Comments

Почему для квадрата не подходит формула S=pr

Вполне подходит. Полупериметр p=2а, r=a/2, откуда S=2a∙(a/2)=a².

Огромное спасибо этому сайту!Всё просто, понятно и правильно.

Радиус вписанной окружности это есть высота правильного многоугольника? Работает ли это для всех многоугольников?

Источник