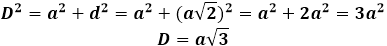Грань куба равна а найдите длину его диагонали

Диагональ куба

Куб является базовым геометрическим телом, когда речь заходит об объеме и объемных телах. Недаром третья степень, которая получается умножением трех одинаковых чисел друг на друга (как при нахождении объема куба — трех его измерений одинаковых измерений) названа в его честь.

Основным и единственным параметром куба является его ребро a,так как все ребра у куба конгруэнтны, и представляют собой одновременно и длину, и ширину, и высоту. Соответственно, всего одно значение определяет все возможные характеристики куба, связанные с его измерениями.

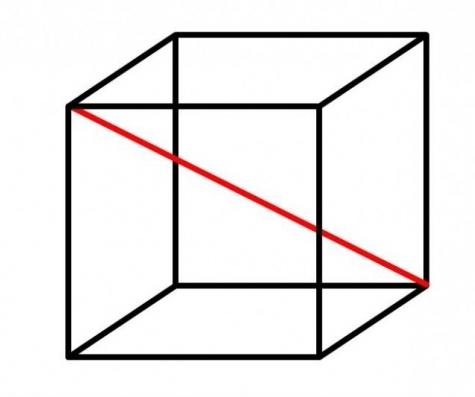
Помимо ребер, вершины куба можно соединить диагоналями. Диагонали могут проходить через грани куба, тогда они будут просто диагональю основания или диагональю квадрата в плоскости, либо диагонали могут быть проведены внутри самого куба, соединяя противоположные основания в крайних точках (вершинах).

Чтобы найти диагональ куба через его ребро, необходимо сначала провести дополнительное построение в виде диагонали одного из соединяемых оснований, тогда диагональ куба станет гипотенузой новоиспеченного прямоугольного треугольника, катетами которого являются ребро куба и диагональ основания. Если ребро куба задано условиями задачи, то диагональ квадрата в основании придется сначала вычислить по формуле: d=a√2

Тогда диагональ куба можно будет выразить через теорему Пифагора, и она примет следующий вид:

Источник

Что такое диагональ куба, и как ее найти

Что такое куб, и какие диагонали он имеет

Куб (правильный многогранник или гексаэдр) представляет собой объемную фигуру, каждая грань – это квадрат, у которого, как нам известно, все стороны равны. Диагональю куба является отрезок, который проходит через центр фигуры и соединяет симметричные вершины. В правильном гексаэдре имеется 4 диагонали, и все они будут равны. Очень важно не путать диагональ самой фигуры с диагональю ее грани или квадрата, который лежит на его основании. Диагональ грани куба проходит через центр грани и соединяет противоположные вершины квадрата.

Формула, по которой можно найти диагональ куба

Диагональ правильного многогранника можно найти по очень простой формуле, которую необходимо запомнить. D=a√3, где D обозначаем диагональ куба, а – это ребро. Приведем пример задачи, где необходимо найти диагональ, если известно, что длина его ребра равна 2 см. Здесь все просто D = 2√3, даже считать ничего не надо. Во втором примере, пусть ребро куба будет равно √3 см, то тогда получаем D = √3√3=√9=3. Ответ: D равен 3 см.

Формула, по которой можно найти диагональ грани куба

Если известна диагональ грани куба

По условию задачи, нам дана только диагональ грани правильного многогранника, которая равна, предположим, √2 см, а нам необходимо найти диагональ куба. Формула решения этой задачи немного сложнее предыдущей. Если нам известно d, то мы можем найти ребро куба, исходя из нашей второй формулы d=a√2. Получаем а= d/√2= √2/√2=1см (это наше ребро). А если известна эта величина, то найти диагональ куба не составит труда: D = 1√3= √3. Вот так мы решили нашу задачку.

Если известна площадь поверхности

Следующий алгоритм решения строится на нахождении диагонали по площади поверхности куба. Предположим, что она равна 72 см 2 . Для начала найдем площадь одной грани, а всего их 6. Значит, 72 необходимо поделить на 6, получаем 12 см 2 . Это площадь одной грани. Чтобы найти ребро правильного многогранника, необходимо вспомнить формулу S=a 2 , значит a=√S. Подставляем и получаем a=√12 (ребро куба). А если мы знаем это значение, то и диагональ найти не сложно D= a√3= √12 √3 = √36 = 6. Ответ: диагональ куба равна 6 см 2 .

Если известна длина ребер куба

Бывают такие случаи, когда в задаче дана только длина всех ребер куба. Тогда необходимо это значение разделить на 12. Именно столько сторон в правильном многограннике. Например, если сумма всех ребер равна 40, то одна сторона будет равна 40/12=3,333. Вставляем в нашу первую формулу и получаем ответ!

Источник

Что такое куб: определение, свойства, формулы

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:

Свойство 2

Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

• a – ребро куба;
• d – диагональ куба или его грани.

Диагональ

Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.

Диагональ грани

Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

Периметр ребер

Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.

Объем

Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара

Радиус шара, описанного около куба, равняется половине его диагонали.

Радиус вписанного шара

Радиус вписанного в куб шара равен половине длины его ребра.

Источник

Решение типовых заданий ЕГЭ второй части задание 14-4

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

(типовые задания С2) — 4 Многогранники: виды задач и методы их решения Методическая разработка Амачкиной А.А. МОУ СОШ №12, г. Балашиха, Московской области.

Для нахождения расстояния между скрещивающимися прямыми можно воспользоваться одним из приведенных ниже четырех способов. 1. Построить общий перпендикуляр двух скрещивающихся прямых (отрезок с концами на этих прямых и перпендикулярный обеим) и найти его длину. Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра. 1.4. Расстояние между скрещивающимися прямыми Поэтапно-вычислительный метод

2. Построить плоскость, содержащую одну из прямых и параллельную второй. Тогда искомое расстояние будет равно расстояние от какой-нибудь точки второй прямой до построенной плоскости. 3. Заключить данные прямые в параллельные плоскости, проходящие через данные скрещивающиеся прямые, и найти расстояние между этими плоскостями. 4. Построить плоскость, перпендикулярную одной из данных прямых, и построить на этой плоскости ортогональную проекцию второй прямой

Пример 19. В кубе, длина ребра которого равна a, найти расстояние между ребром и диагональю, не пересекающей его грани. Решение. В качестве примера найдем расстояние между ребром AA1 и диагональю D1C .Прямые AA1 и D1C — скрещивающиеся. Используя каждый из отмеченных способов, покажем, что расстояние между ними равно a .

1-й способ. Так как то A1D1 –общий перпендикуляр двух скрещивающихся прямых AA1 и D1C . Расстояние между AA1 и DD1C1 равно A1D1 = a

2-й способ. Так как плоскость DD1C1 , содержащая D1C , параллельна AA1 , то расстояние от AA1 до DD1C1 равно a .

3-й способ. Плоскость DD1C1 , содержащая , D1 C параллельна плоскости AA1B1 , содержащей , AA1 и Расстояние между ними равно a .

А C А1 B1 C1 D1 B D 4-й способ. Плоскость ABC перпендикулярна прямой . AA1 Точка A-проекция AA1 на эту плоскость. Проекцией D1C на плоскость ABC является DC. Расстояние от точки A до DC. равно a .

Пример 20. Найти расстояние между непересекающимися диагоналями двух смежных граней куба, длина ребра которого равна a . Решение. Найдем расстояние между диагоналями A1C1 и AD1 куба ABCDA1 B1 C1 D1 .

1-й способ. Пусть отрезок PQ есть общий перпендикуляр скрещивающихся прямых A1C1 и AD1 , а PN и KQ — его ортогональные проекции на плоскости A1B1C1 и AA1D1 соответственно На основании теоремы о трех перпендикулярах

Треугольники A1PN и KQD1 — прямоугольные и равнобедренные, поэтому Тогда из прямоугольного треугольника PNQ получим расстояние между A1C1 и AD1:

2-й способ. Построим плоскость, содержащую AD1 и параллельную A1C1 .Искомой плоскостью является AD1C Найдем расстояние до нее от какой-либо точки прямой A1C1 . Для этого опустим из точки O на указанную плоскость перпендикуляр. Плоскости BB1D1 и AD1C перпендикулярны

Замечание. Для нахождения расстояния от точки О до плоскости AD1C можно воспользоваться результатом примера 10.

3-й способ. Построим параллельные плоскости AD1C и BA1C1 содержащие прямые AD1 и A1C1 соответственно. Диагональ B1D куба перпендикулярна обеим плоскостям и точками K и N делится на три равные части (опорная задача 20). Расстояние между плоскостями AD1C и BA1C1 равно длине отрезка KN, т.е.

4-й способ. Плоскость BB1D1 перпендикулярна прямой A1C1и плоскости AD1C

D1O1 — проекция AD1 на плоскость BB1D1 . Расстояние от точки O (проекции A1C1 на плоскость BB1D1 ) до D1O1 равно длине отрезка ON Пример 21. В правильной усеченной четырехугольной пирамиде ABCDA1 B1 C1 D1 со сторонами оснований равными a и b( a > b ), и высотой h найти расстояние между диагональю BD1 и диагональю большего основания AC .

Решение. Прямые BD1 и AC скрещиваются.Точки O и O1 — точки пересечения диагоналей оснований пирамиды. как отрезок, соединяющий середины оснований равнобедренных трапеций BB1D1D и AA1C1C.

так как AC перпендикулярна двум Построим плоскость перпендикулярную одной из скрещивающихся прямых BD1 и AC . Плоскость пересекающимся прямым этой плоскости: ( ABCD — квадрат) и (OO1 — высота пирамиды). Прямая BD1 лежит в плоскости BB1D1 , поэтому искомое расстояние равно длине перпендикуляра, опущенного из точки O на BD1 . OK найдем из подобия прямоугольных треугольников BD N 1 и BKO, имеющих общий острый угол. В треугольнике BD N 1 : D1N = h ,

Пример 22. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найти расстояние между прямыми BD и SA. Решение. Пусть E – основание перпендикуляра, опущенного из точки O на ребро SA. Так как прямая BD перпендикулярна плоскости AOS, то

Bекторно-координатный метод Таким образом, ОЕ – общий перпендикуляр к скрещивающимся прямым BD и SA. Найдем его длину, вычислив двумя способами площадь треугольника AOS. Из равенства AO* SO = AS *OE, где Пример 23. В единичном кубе ABCDA1B1C1D1 найти расстояние между диагональю куба BD1 и диагональю грани AB1 . Решение. Введем прямоугольную систему координат, тогда А(0; 0; 0) , В(0;1; 0) , В1(0;1;1), D1 (1; 0;1).

Пусть EF – общий перпендикуляр скрещивающихся прямых BD1 и AB1 , то есть ПричемОбозначим и воспользуемся формулами для координат точки (опорная задача 1), которая делит данный отрезок в заданном отношении.

Тогда E(0, p, p) , F(q, 1- q, q) . Так как вектор должен быть перпендикулярным векторам то имеем систему уравнений:

Векторный метод Пример 24. В единичном кубе ABCDA1B1C1D1 найти расстояние между прямыми AB1 и BD . Решение. Пусть Если M и N – основания общего перпендикуляра прямых AB1и BD соответственно, то имеем

Опорная задача Если AB и CD – скрещивающиеся ребра треугольной пирамиды ABCD, d – расстояние между ними, АВ = а , CD =b ,– угол между AB и CD, V – объем пирамиды ABCD, то Пример 25. В единичном кубе ABCDA1 B1 C1 D1 найти расстояние между диагональю куба BD1 и диагональю грани AB1 . Решение. Найдем искомое расстояние по формуле

где V –объем пирамиды ABB1 D1 — угол между прямыми BD1 и AB1 . Так как площадь основания АВВ1 пирамиды ABB1 D1 равна

Используемая литература: Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 596 287 материалов в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Добавить в избранное

• 13.04.2018 2313
• PPTX 392.3 кбайт
• 17 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Амачкина Алла Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Инфоурок стал резидентом Сколково

Минпросвещения упростит процедуру подачи документов в детский сад

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник