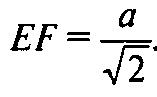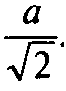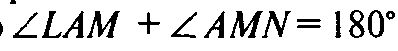Доказать что сечение куба правильный шестиугольник

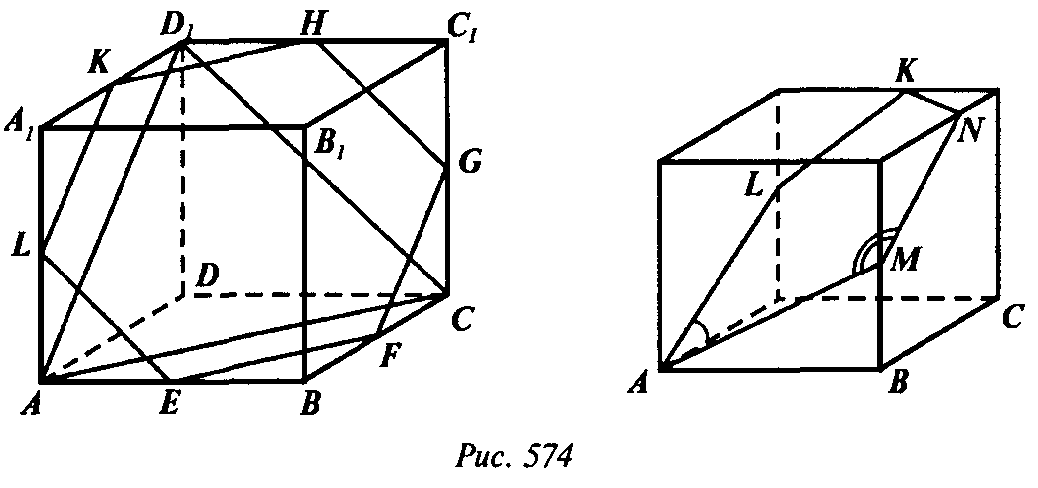
774. Докажите, что сечением куба может быть правильный треугольник, квадрат, правильный шестиугольник, но не может быть правильный пятиугольник и правильный многоугольник с числом сторон более шести.

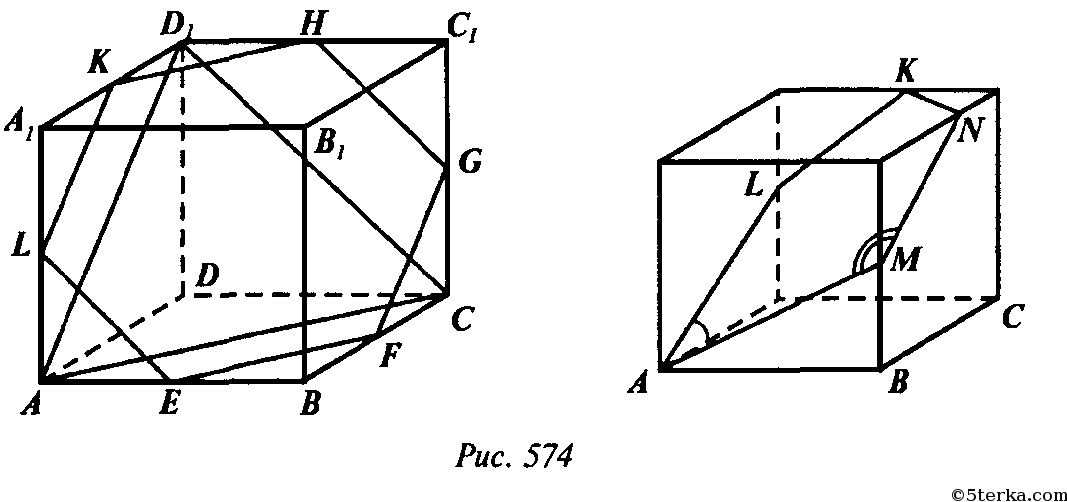
Проведем через середину Е ребра АВ плоскость α || ACD₁ Она пересечет ВС в некоторой точке F.

Так как EF || АС, то по теореме Фалеса F — середина ВС и

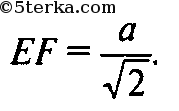
Рассуждая аналогично, получим последовательно, что α

пройдет также через середины G, Н, К, L ребер куба, и все стороны шестиугольника EFGHKL равны

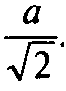
Его углы равны между собой

как соответственные углы треугольников KLE, LEF, EFG, FGH, GHK, HKL, равных друг другу по трем сторонам.

Таким образом — сечение — правильный шестиугольник. Пятиугольное сечение правильным быть не может. Так как в сечении AMNKL AL || MN, то

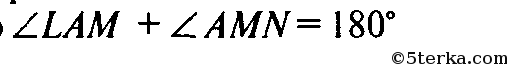
равны, то они — прямые и не равны 108°.

Сечений с семью и более сторонами быть не может, так как граней у куба только шесть.

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №774
к главе «Задачи повышенной трудности».

Источник

Задача 45742 Дан куб ABCDA1B1C1D1. а) Докажите, что.

Условие

а) Докажите, что сечение куба плоскостью, проходящей через центр куба перпендикулярно диагонали АС1 является правильным шестиугольником.

б) Найдите угол между прямой АС1 и плоскостью ВСС1. [14п10]

Решение

Пусть ребро куба равно [b]а.[/b]

a) Диагональ АС_(1) принадлежит плоскости AD_(1)C_(1)B

В прямоугольник AD_(1)C_(1)B:
AD_(1)=BC_(1)=[b]a[/b]*sqrt(2)
AC_(1)=[b]a[/b]*sqrt(3)

Центр куба точка О — точка пересечения диагоналей AC_(1) и BD_(1)

В прямоугольнике AD_(1)C_(1)B:
через точку О — проводим [b]MN[/b] ⊥ AC_(1).
АО=ОС_(1) и ∠ D_(1)AO= ∠ OC_(1)N ⇒ АМ=С_(1)N; D_(1)N=BN

BP=a*sqrt(2)/sqrt(3) (высота прямоугольного треугольника АВС_(1))
По теореме Пифагора АР^2=AB^2-BP^2=a^2-(a*sqrt(2)/sqrt(3))^2=a^2/3 ⇒
AP=a*sqrt(3)/3
Аналогично С_(1)Т=a*sqrt(3)/3;
Тогда PT=AC_(1)-AP-CT=a*sqrt(3)/3
O-середина PT ⇒PO= OT=a*sqrt(3)/6
РО:ОС_(1)=[b]1:3 [/b]⇒ BN:NC_(1)=[b]1:3[/b]

Точка М ∈ грани АD_(1)D, N ∈ BB_(1)C

BN:NC1=[b]1:3[/b] ⇒ BN_(1):N_(1)C=[b]1:3[/b] и DM_(1):M_(1)A=[b]1:3[/b]

По теореме о 3-х перпендикулярах диагональ АС_(1) ⊥ B_(1)C, так как BC_(1)-проекция АС_(1) и BC_(1) ⊥ B_(1)C — диагонали квадрата ВB_(1)C_(1)С

Через точку N проводим EF || B_(1)C.

и АС_(1) перпендикулярна двум пересекающимся прямым
MN и EF пл. MEF

пл. МЕF= α — искомая плоскость сечения.

Плоскость α пересекает грань BC_(1) ⊥ B_(1)C по отрезку ЕF

И так в каждой грани. Все шесть сторон сечения — параллельным соответствующим диагоналям граней куба и равны a*sqrt(2)/2

О т в е т. ∠ АС_(1)B=arctg [b]sqrt(2)/2[/b]

Есть решение cлучая а) координатным методом.
Не мое. Из интернета.
Диагонали BD_(1) и АС_(1) взаимозаменяемы.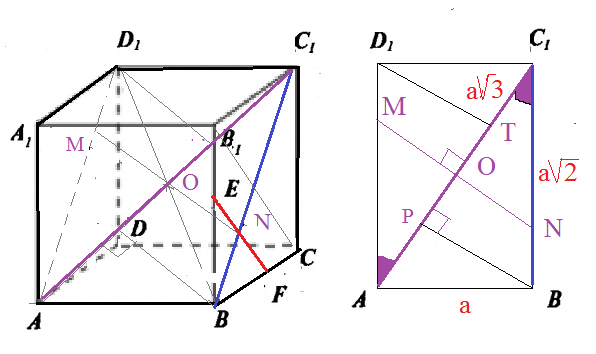

Источник

Меч ниндзя разрезает математический куб пополам

Итак, вопрос.
Разрезав куб на две равные половинки, мы получим в сечении …?
— A: квадрат;
— B: прямоугольник;
— C: ромб;
— D: шестиугольник.

Если вы думаете, что ответ A (квадрат) очевиден и отбрасываете все другие ответы, то делаете большую ошибку. Может показаться, что например, такой вариант ответа как D: (шестиугольник) здесь заведомо лишний. Но это не так. Здесь все варианты ответов верные!

В качестве идеи для этой статьи послужила популярная игра «Fruit ninja». Где необходимо разрезать мечом летящие фрукты. Допустим, что фрукты в большинстве, имеют круглую или овальную форму. Разрезая такие фрукты на половинки, обратите внимание, что будет в месте разреза. Какая геометрическая форма? Если мы разрезаем точно и быстро, то будет сечение в форме круга или овала.
А как вам предложение разрезать классический куб ? Здесь уже придется подумать.
Но мы ещё усложним задачу. Задача разрезать куб таким образом, чтобы после разреза получились равные половинки.

Как продемонстрировать, что это возможно? Как доказать, что куб можно разрезать на две равные половинки?
Для этого мы рассмотрим каждый вариант ответа и изготовим модели кубов состоящие из двух половинок.
У нас будет развёртка только одной половинки, чтобы исключить всякие сомнения.
А как же вторая половинка?
Вторая половинка должна быть точно такая же, как и первая. Тогда утверждение будет доказано.
Просто ещё раз соберите половинку из этой же развёртки.
Сложите половинки вместе, и вы получите исходный куб!

Источник

Многоугольники получающиеся в сечении куба

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Многоугольники
получающиеся
в сечении куба

Цель работы:
Продемонстрировать плоские многоугольники,
которые получаются при сечение
куба плоскостью,
выяснить их вид
и доказать это исходя из основных
теорем и аксиом.

Доказать, что если в сечение куба получится треугольник, то этот треугольник остроугольный.
Задача №1
Пусть ABCDA1B1C1D1 – куб, MNP – сечение куба плоскостью.
Обозначим: AN=x, AP=y, AM=z.
Тогда .
Рассмотрим треугольник MNP с углами , , и применим теорему косинусов:

Из последнего равенства, очевидно, что
cos >0, следовательно,

Курс повышения квалификации

Охрана труда

Курс профессиональной переподготовки

Охрана труда

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 595 632 материала в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Добавить в избранное

• 25.01.2020 398
• PPTX 241 кбайт
• 0 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Федяева Наталья Ивановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Минпросвещения упростит процедуру подачи документов в детский сад

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

В Швеции запретят использовать мобильные телефоны на уроках

Минпросвещения России подготовит учителей для обучения детей из Донбасса

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

774. Докажите, что сечением куба может быть правильный треугольник, квадрат, правильный шестиугольник, но не может быть правильный пятиугольник и правильный многоугольник с числом сторон более шести

Задачи повышенной трудности → номер 774

Если ABCDA1B1C1D1— куб с ребром a, то его сечение ACD1 — правильный треугольник, а любое сечение — параллельное грани — квадрат (рис. 574).

Проведем через середину Е ребра АВ плоскость α || ACD1 Она пересечет ВС в некоторой точке F.

Так как EF || АС, то по теореме Фалеса F — середина ВС и

Рассуждая аналогично, получим последовательно, что α

Пройдет также через середины G, Н, К, L ребер куба, и все стороны шестиугольника EFGHKL равны

Его углы равны между собой

Как соответственные углы треугольников KLE, LEF, EFG, FGH, GHK, HKL, равных друг другу по трем сторонам.

Таким образом — сечение — правильный шестиугольник. Пятиугольное сечение правильным быть не может. Так как в сечении AMNKL AL || MN, то

Равны, то они — прямые и не равны 108°.

Сечений с семью и более сторонами быть не может, так как граней у куба только шесть.

Источник

Доказать что сечение куба правильный шестиугольник

а) Докажите, что сечение куба плоскостью KLM является правильным многоугольником.

б) Найдите расстояния от точки A до плоскости KLM, если ребро куба равно 2.

а) Так как плоскость KLM пересекает рёбра AB, B₁C₁ и DD₁, она должна также пересекать рёбра C₁D₁, AD и BB₁. Назовём точки пересечения Q, R, P соответственно. Таким образом, в сечении получаем шестиугольник KPLQMR. Пусть плоскость сечения пересекает ребро AA₁ в точке S, тогда через неё проходят прямые KP и MR. Так как грани куба параллельны, то прямые KP и MQ также параллельны, следовательно, так как AK = KB = MD₁, треугольники KSA, KPB и MQD₁ равны.

Далее, с одной стороны, углы MQD, SKD и PKB равны как углы между парами параллельных прямых, с другой стороны, углы MQD и KPB равны как углы, лежащие напротив равных сторон. Следовательно, углы PKB и KPB равны, и указанные треугольники равнобедренные: BK = BP, D₁M = D₁Q, P — середина BB₁, Q — середина C₁D₁, R — середина AD. Таким образом, KP = PL = LQ = QM = MR = RK.

Заметим теперь, что KL = PQ = LM = QR = MK = RP, поэтому равнобедренные треугольники KPL, PLQ, LQM, QMR, MRK, RKP и углы шестиугольника равны. Следовательно, KPLQMR — правильный шестиугольник.

б) Рассмотрим пирамиду SAKR и запишем её объём двумя способами:

где h_A — искомое расстояние, AS = AK = AR = 1, Далее,

Ответ: б)

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Источник Оцените статью Вам также может понравиться datchik-temperaturi-vxodyashego-vozduxa-vaz-2114-gde—t7zjvf9u ����JFIF«��C (1#%(:3=Mqypdx\egc��C//cB8Bcccccccccccccccccccccccccccccccccccccccccccccccccc����» 0174 Что за датчик 89747 52010 на Toyota и как он работает 89747 52010 toyota что это за датчик В автомобилях 0209 Где находится датчик распредвала двигателя Волга 406? Волга 406 двигатель где находится датчик распредвала 0148 Где находится датчик детонации на Ford Mondeo 3: подробная инструкция Где находится датчик детонации форд мондео 3 Датчик 0236 Где находится датчик распредвала ГАЗель двигатель 4216? Где находится датчик распредвала газель двигатель 4216 0149 Где находится датчик электронной педали газа на ВАЗ 2114: местоположение и проблемы Где находится датчик электронной педали газа ваз 2114 0263 Где расположены датчики температуры двигателя Audi A6 C5? Где находятся датчики температуры двигателя ауди а6 0150 Где находится датчик абсолютного давления во впускном коллекторе Tiguan? Датчик абсолютного давления во впускном коллекторе 0175 Adblock detector