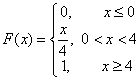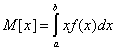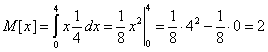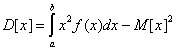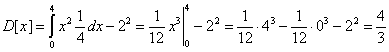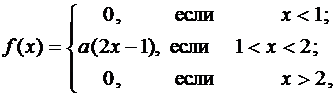- Непрерывная случайная величина
- Примеры решений
- Математическое ожидание непрерывной случайной величины. Пример решения
- Математическое ожидание непрерывной случайной величины
- Свойства плотности распределения
- Двумерная непрерывная случайная величина
- Система непрерывных случайных величин: теория
- Примеры решений
- Решебник по теории вероятности онлайн
- Формулы онлайн: Случайные величины
- Каталог формул по теории вероятности онлайн
- Случайные величины. Способы задания
- Ряд распределения дискретной случайной величины
- Функция распределения (интегральная функция распределения)
- Плотность распределения (дифференциальная функция распределения)
- Вероятность попадания случайной величины в заданный интервал
- Случайные величины. Числовые характеристики
- Математическое ожидание случайной величины
- Дисперсия случайной величины
- Среднее квадратическое отклонение случайной величины
- Коэффициент вариации случайной величины
- Начальный момент r–го порядка случайной величины
- Центральный момент r – го порядка случайной величины
- Асимметрия
- Эксцесс
- Решенные задачи по теории вероятностей
- Равномерно распределенная случайная величина
- Примеры решений
- Решебник по теории вероятности онлайн
Непрерывная случайная величина
Ранее мы представили примеры решений задач о дискретной случайной величине, теперь переходим к непрерывной. Формально в задачах требуется найти тоже самое: вычислить числовые характеристики, начертить графики, определить неизвестные параметры, найти вероятности событий.
Но формулы-то совсем другие (в силу непрерывности СВ), поэтому стоит разобраться в них хорошенько. Надеемся, наши примеры вам помогут (а если нет времени, закажите решение).
Ниже вы найдете примеры решений на самые разные законы распределений непрерывных случайных величин: законы $\arcsin$ и $\arctan$, тригонометрические и логарифмические функции, показательный, равномерный закон распределения, законы Коши, Симпсона, Лапласа и т.д.
Примеры решений
Задача 1. Случайная величина X задана дифференциальной функцией распределения 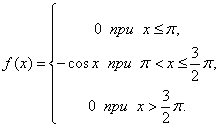
1) Определить вероятность попадания случайной величины X в интервал $[\pi, 5/4 \pi]$.
2) Найти математическое ожидание и дисперсию случайной величины X.
Задача 2. Случайная величина X задана плотностью вероятности: 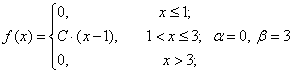
Требуется:
а) найти коэффициент C;
б) найти функцию распределения F(x);
в) найти M(X), D(X), σ(X)
г) найти вероятность P(α -2t при t ≥ 0 и f(t)=0 при t Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Математическое ожидание непрерывной случайной величины. Пример решения
Задание 2. Найти дисперсию случайной величины X , заданной интегральной функцией.
Задание 3. Найти математическое ожидание случайной величины Х заданной функцией распределения.
Задание 4. Плотность вероятности некоторой случайной величины задана следующим образом: f(x) = A/x 4 (x = 1; +∞)
Найти коэффициент A , функцию распределения F(x) , математическое ожидание и дисперсию, а также вероятность того, что случайная величина примет значение в интервале [0,2]. Построить графики f(x) и F(x) .
Задача. Функция распределения некоторой непрерывной случайной величины задана следующим образом:
Определить параметры a и b , найти выражение для плотности вероятности f(x) , математическое ожидание и дисперсию, а также вероятность того, что случайная величина примет значение в интервале [2,3]. Построить графики f(x) и F(x).
- Решение
- Видео решение
Случайная величина Х задана плотностью распределения f(x):
Пример №2 . Случайная величина X задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Схематично построить графики функций F(x) и f(x).
Математическое ожидание непрерывной случайной величины
Дисперсия непрерывной случайной величины X ( Var[X] ), возможные значения которой принадлежат всей оси Ох , определяется равенством:
Назначение сервиса . Онлайн калькулятор предназначен для решения задач, в которых заданы либо плотность распределения f(x) , либо функция распределения F(x) (см. пример). Обычно в таких заданиях требуется найти математическое ожидание, среднее квадратическое отклонение, построить графики функций f(x) и F(x) .
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
- Типовые задания
Задана функция распределения F(x):
Непрерывная случайна величина задана плотностью вероятностей
(закон распределения Релея – применяется в радиотехнике). Найти M(x) , D(x) .
- Примеры
В качестве неизвестного параметра используйте заглавную букву A . Например, c(x 2 +2x-1) ≡ A*(x^2+2*x-1)?>
≡ x^2/(1+x)
cos 2 (2x+1) ≡ (cos(2*x+1))^2≡ 1+(x-2)^(2/3)
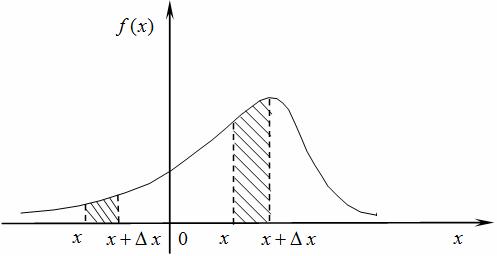
Случайную величину X называют непрерывной, если ее функция распределения F(X)=P(X f(x)=F’(x) , производная от функции распределения.
Свойства плотности распределения
Пример №1 . Случайная величина Х задана функцией распределения F(x) :
Найдем плотность распределения f(x), как производную от функции распределения F(x):
f(x) = dF(x)/dx = 1 /4
Математическое ожидание.
Дисперсия.
Пример №2 . Плотность распределения непрерывной случайной величины X имеет вид
Пример №3 . Непрерывная случайная величина имеет плотность распределения f(x). Найти величину с, интегральную функцию распределения, математическое ожидание и среднее квадратическое отклонение этой случайной величины.
Примечание. Очень часто при нахождении математического ожидания и дисперсии применяют формулу интегрирования по частям.
Двумерная непрерывная случайная величина
Ранее мы разобрали примеры решений задач для одномерной непрерывной случайной величины. Перейдем к более сложному случаю — двумерной непрерывной случайной величине $(X,Y)$ (или двумерному вектору). Кратко выпишем основы теории.
Система непрерывных случайных величин: теория
Двумерная непрерывная СВ задается своей функцией распределения $F(x,y)=P(X\lt x, Y\lt y)$, свойства которой аналогичны свойствам одномерной ФР. Эта функция должна быть непрерывна, дифференцируема и иметь вторую смешанную производную, которая будет как раз плотностью распределения вероятностей системы непрерывных случайных величин:
Зная плотность совместного распределения, можно найти одномерные плотности для $X$ и $Y$:
Вероятность попадания случайного вектора в прямоугольную область можно вычислить как двойной интеграл от плотности (по этой области) или через функцию распределения:
$$P(x_1 \le X \le x_2, y_1 \le Y \le y_2) = F(x_2, y_2)-F(x_1, y_2)-F(x_2, y_1)+F(x_1, y_1).$$
Как и для случая дискретных двумерных СВ вводится понятие условного закона распределения, плотности которых можно найти так:
Если для всех значений $(x,y)$ выполняется равенство
то случайные величины $X, Y$ называются независимыми (их условные плотности распределения совпадают с безусловными). Для независимых случайных величин выполняется аналогичное равенство для функций распределений:
Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:
В этом разделе мы приведем примеры задач с полным решением, где используются непрерывные двумерные случайные величины (системы случайных величин).
Примеры решений
Задача 1. Дана плотность распределения вероятностей системы $$ f(x)= \left\< \begin
$C, \rho_1(x), \rho_2(y), m_x, m_y, D_x, D_y, cov(X,Y), r_
Задача 2. Дана плотность распределения $f(x,y)$ системы $X,Y$ двух непрерывных случайных величин в треугольнике АВС.
1.1. Найдите константу с.
1.2. Найдите $f_X(x), f_Y(y)$ — плотности распределения с.в. Х и с.в. Y.
Выясните, зависимы или нет с.в. Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.
1.3. Найдите математическое ожидание и дисперсию с.в. Х и с.в. Y. Поясните смысл найденных характеристик.
1.4. Найдите коэффициент корреляции с.в. Х и Y. Являются ли случайные величины коррелированными? Сформулируйте свойства коэффициента корреляции.
1.5. Запишите уравнение регрессии с.в. Y на Х и постройте линию регрессии в треугольнике АВС.
1.6. Запишите уравнение линейной среднеквадратичной регрессии с.в. Y на Х и постройте эту прямую в треугольнике АВС. $$ f(x,y)=c\sqrt
Задача 3. Интегральная функция распределения случайного вектора (X,Y): $$ F(x)= \left\< \begin
Задача 4. Плотность совместного распределения непрерывной двумерной случайной величины (Х, У) $$f(x,y)=C e^<-x^2-2xy-4y^2>$$ Найти:
а) постоянный множитель С;
б) плотности распределения составляющих;
в) условные плотности распределения составляющих.
Задача 5. Задана двумерная плотность вероятности системы двух случайных величин: $f(x,y)=1/2 \sin(x+y)$ в квадрате $0 \le x \le \pi/2$, $0 \le y \le \pi/2$, вне квадрата $f(x,y)=0$. Найти функцию распределения системы (X,Y).
Задача 6. Определить плотность вероятности, математические ожидания и корреляционную матрицу системы случайных величин $(X,Y)$, заданных в интервалах $0 \le x \le \pi/2$, $0 \le y \le \pi/2$, если функция распределения системы $F(x,y)=\sin x \sin y$.
Задача 7. Плотность вероятности системы случайных величин равна $$f(x,y) = c(R-\sqrt
А) постоянную $c$;
Б) вероятность попадания в круг радиуса $a\lt R$, если центры обоих кругов совпадают с началом координат.
Задача 8. Совместная плотность вероятности системы двух случайных величин X и Y $$f(x,y)=\frac
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Формулы онлайн: Случайные величины
В данном разделе вы найдете формулы по теории вероятностей в онлайн-варианте (в формате для скачивания — см. на странице Таблицы и формулы по теории вероятностей).
Каталог формул по теории вероятности онлайн
Случайные величины. Способы задания
Ряд распределения дискретной случайной величины
$$ \begin
Сумма вероятностей всегда равна 1 (условие нормировки):
Функция распределения (интегральная функция распределения)
Функция распределения случайной величины $X$ определяется по формуле $F(x)=P(X\lt x)$. Это неубывающая функция, принимающая значения от 0 до 1. Если задана плотность распределения $f(x)$, то функция распределения выражается как интеграл от плотности:
Плотность распределения (дифференциальная функция распределения)
Плотность распределения случайной величины $X$ определяется по формуле $f(x)=F'(x)$. Существует только для непрерывной случайной величины. Для нее выполняется условие нормировки (площадь под кривой вероятности равна 1):
Вероятность попадания случайной величины в заданный интервал
Может быть вычислена двумя способами:
1) через функцию распределения
$$P(\alpha \lt X \lt \beta) = F(\beta)-F(\alpha).$$
2) через плотность распределения
Случайные величины. Числовые характеристики
Математическое ожидание случайной величины
1) Для дискретной случайной величины $X$, заданной рядом распределения:
2) Для непрерывной случайной величины $X$, заданной плотностью распределения:
Дисперсия случайной величины
По определению дисперсия – это второй центральный момент:
$$ D(X) =M\left[ \left(X-M(X)\right)^2 \right] =M(X^2)-\left(M(X)\right)^2.$$
1) Для дискретной случайной величины $X$:
$$ D(X)= \sum_
2) Для непрерывной случайной величины $X$:
Среднее квадратическое отклонение случайной величины
Коэффициент вариации случайной величины
Начальный момент r–го порядка случайной величины
В частности, первый начальный момент – это математическое ожидание: $\nu_1=M(X^1)=M(X).$
Центральный момент r – го порядка случайной величины
$$\mu_r = M\left[ \left(X-M(X)\right)^r \right]$$
В частности, второй центральный момент – это дисперсия:
$$\mu_2 = M\left[ \left(X-M(X)\right)^2 \right] = D(X).$$
Асимметрия
Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого (правая часть кривой более пологая), и отрицателен в противном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.
Эксцесс
Коэффициент эксцесса нормального распределения равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик гладкий.
Решенные задачи по теории вероятностей
Нужна готовая задача по терверу? Найдите на сайте-решебнике:
Равномерно распределенная случайная величина
На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ — распределенных по равномерному закону.
В сущности, равномерное распределение — самое простое из семейства непрерывных, и определяется тем, что плотность распределения постоянна (равна константе) на всем интервале: $f(x)=c=\frac<1>
$$ f(x)= \left\< \begin
Функция распределения для нее вычисляется практически в уме:
$$ F(x)= \left\< \begin
Для равномерного на интервале $(a;b)$ распределения известны формулы для числовых характеристик. Математическое ожидание $M(X)=\frac
В жизни равномерным распределением часто моделируют время ожидания транспорта, ошибки округления в пределах цены деления.
В этом разделе мы приведем разные примеры задач с полным решением, где используются равномерно распределенные случайные величины.
Примеры решений
Задача 1. Автобусы идут с интервалом 5 минут. Полагая, что случайная величина $\xi$ — время ожидания автобуса на остановке — распределена равномерно на указанном интервале, найти среднее время ожидания и среднеквадратическое уклонение времени ожидания.
Задача 2. Телефонный звонок должен последовать от 10 ч до 10 ч 20 мин. Какова вероятность того, что звонок произойдет в последние 10 мин указанного промежутка, если момент звонка случаен?
Задача 3. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.
Задача 4. В здании областной администрации случайное время ожидания лифта равномерно распределено в диапазоне от 0 до 3 минут. Найти а) плотность распределения времени ожидания, б) вероятность ожидания лифта более чем 2 минуты, в) вероятность того, что лифт прибудет в течение первых 15 секунд, г) среднее время ожидания лифта и дисперсию времени ожидания.
Задача 5. Случайная величина $X$ задана интегральной $F(x)$ или дифференциальной $f(x)$ функцией. Требуется:
а) найти параметр $C$;
б) при заданной интегральной функции найти дифференциальную функцию; а при заданной дифференциальной функции найти интегральную функцию;
в) построить графики функций $F(x)$ и $f(x)$;
г) найти математическое ожидание $M[X]$ дисперсию $D[X]$ среднее квадратическое отклонение $\sigma[X]$;
д) вычислить вероятность попадания в интервал $P(a\lt X \lt b)$;
е) определить, квантилем какого порядка является точка $x_p$;
ж) вычислить квантиль порядка $p$.
Задача 6. Дана плотность распределения $p(x)$ случайной величины $\xi$. Найти параметр $\gamma$, математическое ожидание $M\xi$, дисперсию $D\xi$, функцию распределения случайной величины $\xi$, вероятность выполнения неравенства $x_1 \lt \xi \lt x_2$. $$a=1, b=1,8, x_1=1,3, x_2=1,6.$$ $$ p(x)= \left\< \begin
Задача 7. Случайная величина Х равномерно распределена в интервале (1;8). Найти:
а) дифференциальную функцию,
б) интегральную функцию,
в) математическое ожидание, дисперсию и среднее квадратическое отклонение,
г) вероятность попадания в интервал (3;5).
Задача 8. Функция распределения непрерывной случайной величины задана следующим образом: $$ F(x)= \left\< \begin
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:


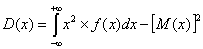

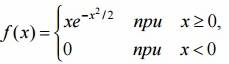
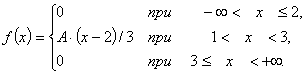
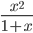 ≡ x^2/(1+x)
≡ x^2/(1+x) 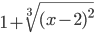 ≡ 1+(x-2)^(2/3)
≡ 1+(x-2)^(2/3)