- Что такое скрещивающиеся ребра куба
- Куб — свойства, виды и формулы
- Элементы куба
- Грань
- Ребро
- Вершина
- Центр грани
- Центр куба
- Ось куба
- Диагональ куба
- Диагональ грани куба
- Объем куба
- Периметр куба
- Площадь поверхности
- Сфера, вписанная в куб
- Сфера, описанная вокруг куба
- Координаты вершин куба
- Свойства куба
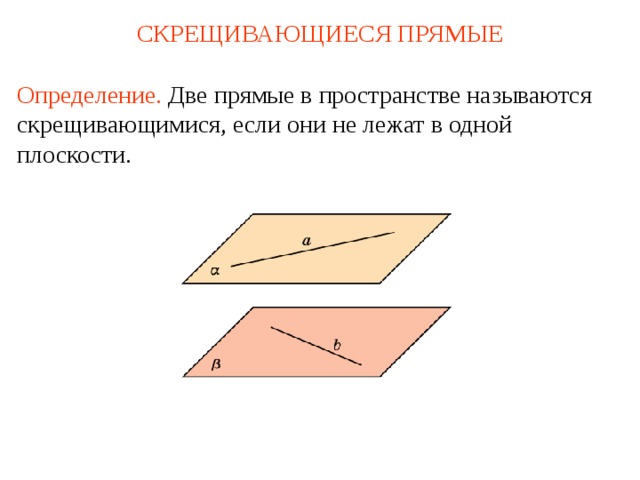
- Скрещивающиеся прямые
- Просмотр содержимого документа «Скрещивающиеся прямые»
Что такое скрещивающиеся ребра куба
ПРЯМАЯ ПРИЗМА. ПОВЕРХНОСТЬ И ОБЪЁМ ПРЯМОЙ ПРИЗМЫ.
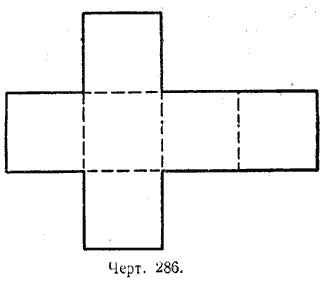
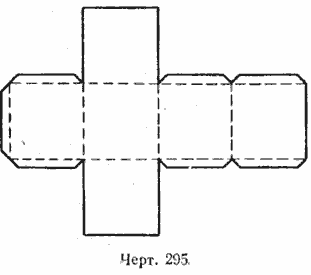
На чертеже 286 изображена выкройка, или, как её принято называть, развёртка геометрического тела. Она состоит из шести равных квадратов. Если эту развёртку согнуть надлежащим образом по указанным на чертеже пунктирным линиям, то мы получим геометрическое тело, называемое кубом.
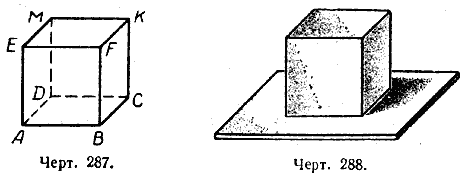
Под номером 287 дан чертёж куба, а под номером 288 дан рисунок куба. Куб ограничен шестью равными квадратами, которые называются его гранями.
На рисунке видны только три его грани, а на чертеже можно видеть все шесть граней. Любые две противоположные грани куба называются его основаниями, тогда остальные четыре его грани называются боковыми гранями; отрезки, которые получаются при пересечении граней куба, называются его рёбрами. У куба 12 рёбер. Все они равны между собой.При пересечении трёх граней куба образуются точки, которые называются его в е р ш и н а м и. У куба 8 вершин.
2. Взаимное положение рёбер и граней куба.
Противоположные грани куба параллельны. Плоскости, в которых лежат эти грани, не пересекаются, т. е. не имеют общих точек. Параллельные плоскости мы наблюдаем на многих окружающих нас предметах; например, плоскости пола и потолка в комнате параллельны.
В кубе можно наблюдать и пересекающиеся плоскости. Пересекаясь, плоскости образуют двугранные углы. Модель двугранных углов можно получить, сгибая лист картона или бумаги по прямой линии.
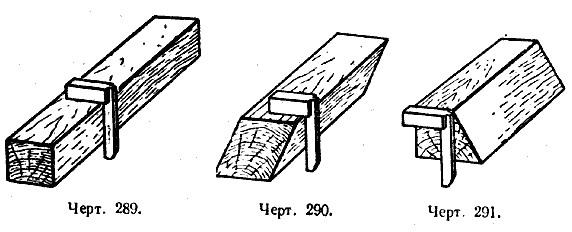
Двугранные углы можно получить острые, прямые и тупые. Грани куба пересекаются под прямым углом. Под прямым углом пересекаются также стены в комнате, стены и потолок, стены и пол. Плоскости, пересекающиеся под прямым углом, называются перпендикулярными. Перпендикулярность плоскостей проверяется с помощью угольника. На чертеже 289 плоскости при пересечении образуют прямой угол. На чертеже 290 и на чертеже 291 показаны плоскости, которые при пересечении не образуют прямого угла; в первом случае они пересекаются под острым углом, во втором случае — под тупым.
Рёбра куба, находящиеся на одной грани (черт. 287), или пересекаются под прямым углом (ЕА _|_ АВ, КС _|_ ВС и т. д.), или параллельны (ЕF || АВ, ВС || КF и т. д.).
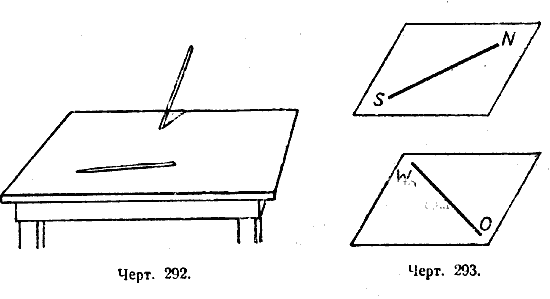
Рёбра куба, например КС и АВ (черт. 287), не параллельны, но и не пересекутся, сколько бы их ни продолжать. Прямые, которые не параллельны и не пересекаются, называются скрещивающимися. Легко получить модели скрещивающихся прямых. Например, две иглы, из которых одна положена на стол, а другая воткнута в стол так, что не пересекает первую, представляют собой модель двух скрещивающихся прямых (черт. 292). Эти две прямые не пересекаются и не параллельны; легко убедиться, что через них нельзя провести плоскость.
Точно так же, если взять две дощечки, поместить их параллельно друг другу и затем на одну из них положить палочку в направлении, например, с юга на север, а на другую — в направлении с запада на восток, то эти две палочки образуют модель скрещивающихся прямых (черт. 293).
Эти две прямые тоже не пересекаются, не параллельны, и через них также нельзя провести плоскость.
Найдите модели скрещивающихся прямых на окружающих предметах, например, в классной комнате.
4. Прямая, перпендикулярная к плоскости.
Рассматривая куб (черт. 287), заметим, что ребро FВ образует прямые углы с рёбрами ВС и АВ, лежащими на нижнем основании куба. Это же ребро FВ образует прямые углы с любой прямой, проведённой в плоскости основания куба через точку В. Ребро FВ является перпендикуляром к плоскости основания куба.
Перпендикуляром к плоскости называется прямая, которая пересекает плоскость в какой-нибудь точке и перпендикулярна к любой прямой, проведённой в этой плоскости через ту же точку.
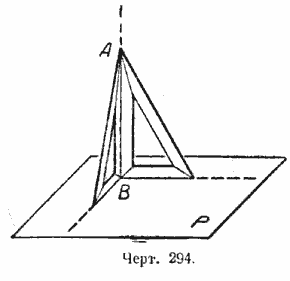
Чтобы провести перпендикуляр к плоскости, берут два чертёжных треугольника и ставят их так, чтобы два катета лежали на плоскости, как показано на чертеже 294, а другую пару катетов совмещают. Эти два катета и образуют перпендикуляр к данной плоскости.
На чертеже 294 прямая АВ перпендикулярна к плоскости Р.
Перпендикулярность прямой АВ к плоскости Р легко проверить: для этого надо взять ещё один чертёжный треугольник и несколько раз в различных положениях приложить его к двум первым треугольникам так, чтобы его катет всякий раз совмещался с катетом АВ. Тогда другой катет третьего треугольника всё время будет находиться в плоскости Р. Значит, можно считать проверенным, что прямая АВ образует прямые углы с любой прямой, проведённой на плоскости через её основание, т. е. является перпендикуляром к плоскости.
Таким образом, мы приходим к выводу: если прямая, пересекающая плоскость в какой-нибудь точке О, перпендикулярна к двум прямым, проведённым на плоскости через точку О, то эта прямая перпендикулярна к плоскости.
Этот вывод является признаком перпендикулярности прямой к плоскости.
Через любую произвольно взятую точку можно провести перпендикуляр к данной плоскости, но только один.
Длина перпендикуляра, опущенного из какой-нибудь точки на плоскость, называется расстоянием от этой точки до плоскости.
5. Площадь поверхности куба.
Чтобы вычислить площадь поверхности куба, достаточно вычислить площадь одной его грани и полученное число помножить на 6. Если ребро куба обозначить через а, то площадь поверхности одной его грани будет равна а 2 , а площадь всей поверхности куба (полная поверхность) составит 6а 2 .
S = 6а 2 , где S — площадь полной поверхности куба.
Площадь поверхности его оснований составит 2а 2 . Площадь поверхности боковых его граней составит 4а 2 .
1. Ребро куба равно 8 см (10 см, 12 см, 20 см). Вычислить площадь всей его поверхности; площадь оснований; площадь его боковой поверхности.
2. Площадь полной поверхности куба равна 150 кв. см (600 кв. см, 216 кв. см, 864 кв. см). Вычислить длину его ребра.
3. Площадь боковой поверхности куба равна 100 кв. см (64 кв. см, 324 кв. см, 576 кв. см). Вычислить площадь его полной поверхности.
4. Сделать из плотной бумаги модель куба, ребро которого равно 8 см.
Указание. Для того чтобы полученное геометрическое тело сохраняло свою форму, у развёртки куба необходимо сделать небольшие закраины (черт. 295). Если их подклеить, они составят каркас, который придаст необходимую жёсткость модели.
5. Сколько потребуется белил для окраски с обеих сторон бака (без крышки), имеющего форму куба с ребром в 80 см, если на окраску 1 кв.м требуется белил 0,25 кг?
Куб — свойства, виды и формулы
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
один центр и несколько осей симметрии.
Скрещивающиеся прямые

10 класс Презентация будет полезна учителям и учащимся.
Просмотр содержимого документа
«Скрещивающиеся прямые»
Определение. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
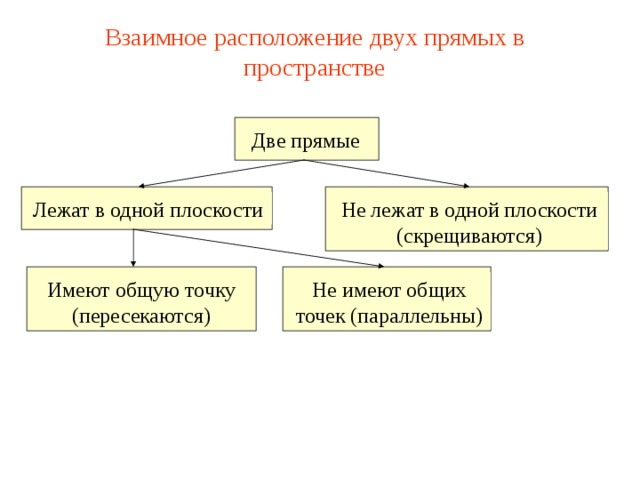
Взаимное расположение двух прямых в пространстве
Не лежат в одной плоскости (скрещиваются)
Имеют общую точку (пересекаются)
Не имеют общих точек (параллельны)
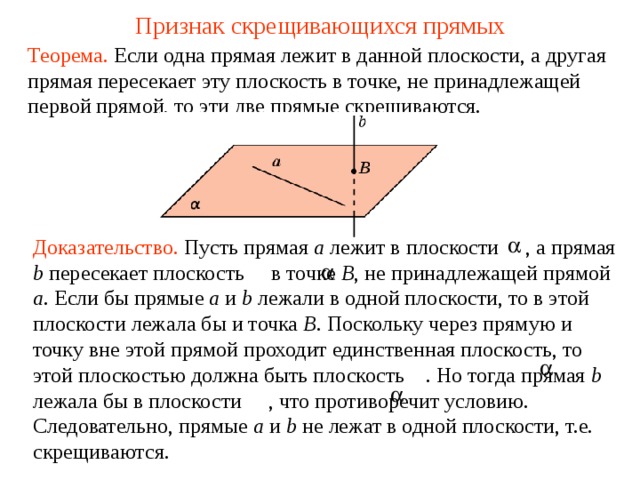
Признак скрещивающихся прямых
Теорема. Если одна прямая лежит в данной плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти две прямые скрещиваются.
Доказательство. Пусть прямая a лежит в плоскости , а прямая b пересекает плоскость в точке B , не принадлежащей прямой a . Если бы прямые a и b лежали в одной плоскости, то в этой плоскости лежала бы и точка B . Поскольку через прямую и точку вне этой прямой проходит единственная плоскость, то этой плоскостью должна быть плоскость . Но тогда прямая b лежала бы в плоскости , что противоречит условию. Следовательно, прямые a и b не лежат в одной плоскости, т.е. скрещиваются.
Всегда ли две не пересекающиеся прямые в пространстве скрещиваются?
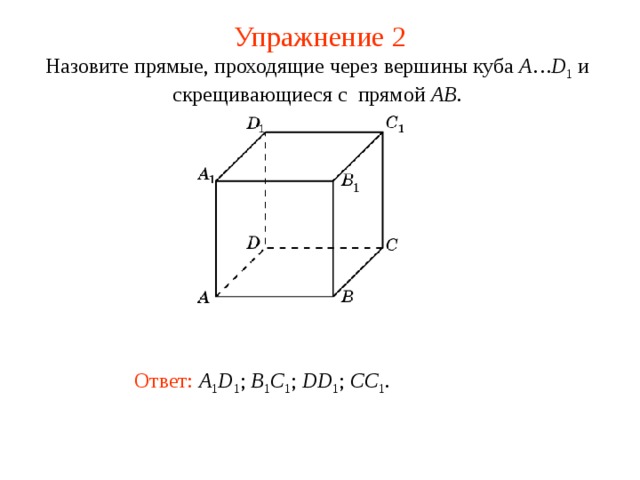
Назовите прямые, проходящие через вершины куба A…D 1 и скрещивающиеся с прямой AB .
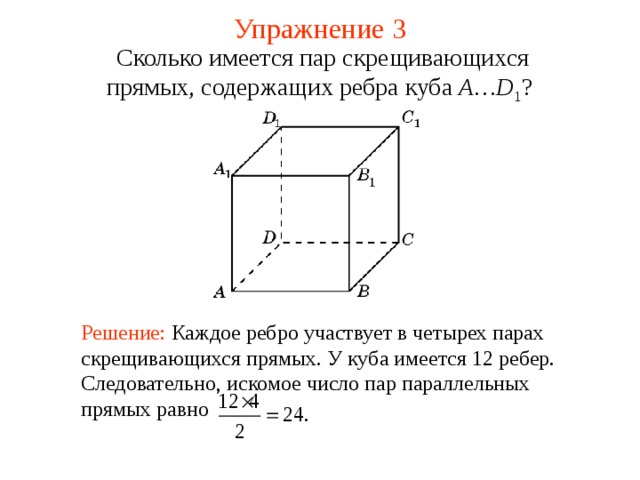
Сколько имеется пар скрещивающихся прямых, содержащих ребра куба A…D 1 ?
Решение: Каждое ребро участвует в четырех парах скрещивающихся прямых. У куба имеется 12 ребер. Следовательно, искомое число пар параллельных прямых равно
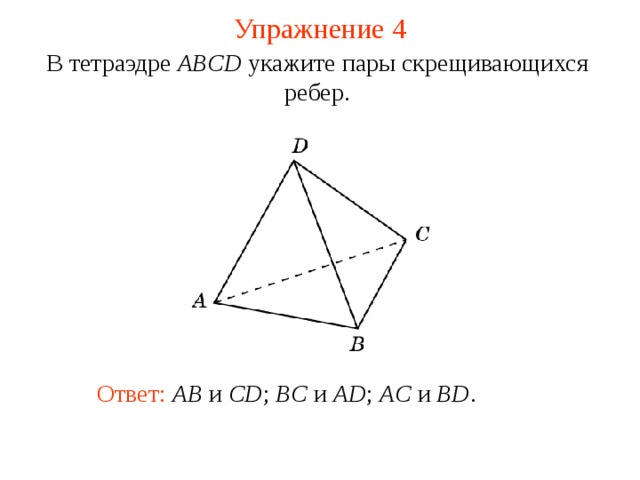
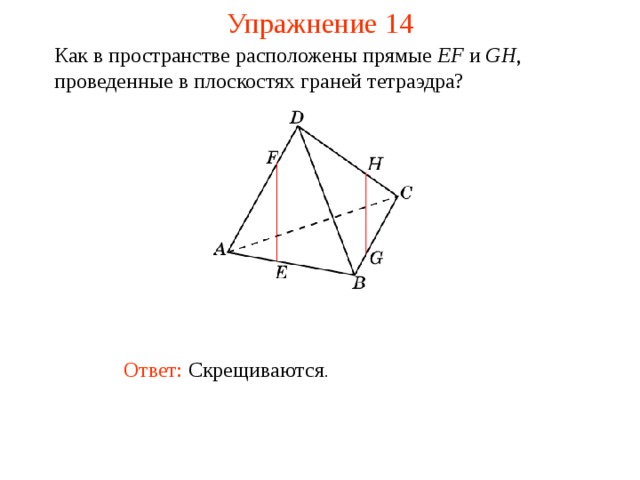
В тетраэдре ABCD укажите пары скрещивающихся ребер.
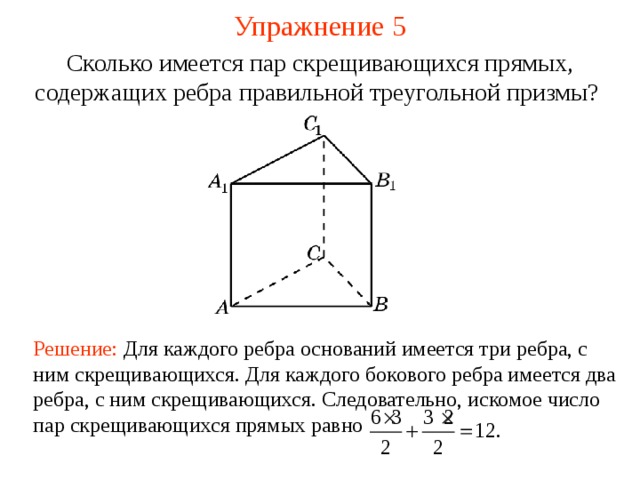
Сколько имеется пар скрещивающихся прямых, содержащих ребра правильной треугольной призмы?
Решение: Для каждого ребра оснований имеется три ребра, с ним скрещивающихся. Для каждого бокового ребра имеется два ребра, с ним скрещивающихся. Следовательно, искомое число пар скрещивающихся прямых равно
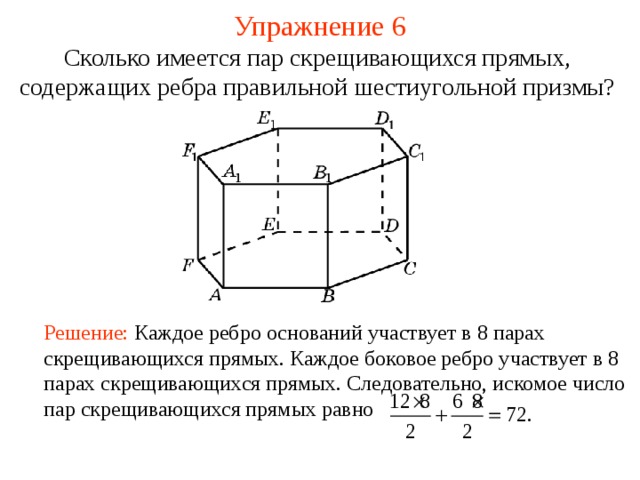
Сколько имеется пар скрещивающихся прямых, содержащих ребра правильной шестиугольной призмы?
Решение: Каждое ребро оснований участвует в 8 парах скрещивающихся прямых. Каждое боковое ребро участвует в 8 парах скрещивающихся прямых. Следовательно, искомое число пар скрещивающихся прямых равно
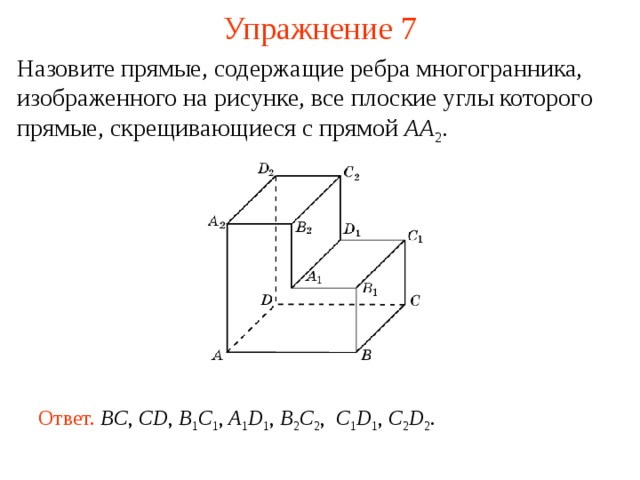
Назовите прямые, содержащие ребра многогранника, изображенного на рисунке, все плоские углы которого прямые, скрещивающиеся с прямой AA 2 .
В режиме слайдов ответ появляется после кликанья мышкой
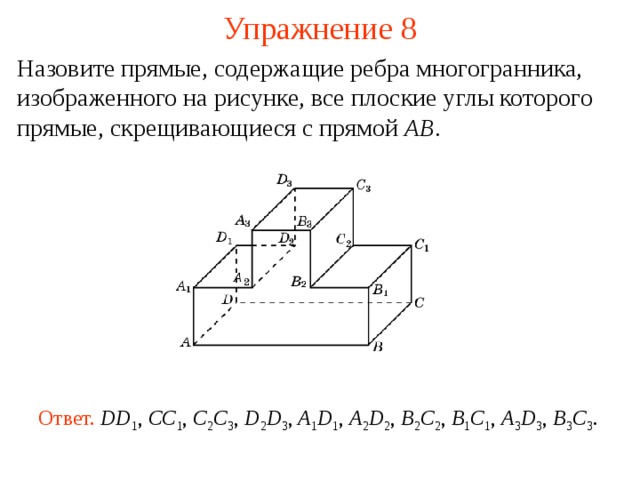
Назовите прямые, содержащие ребра многогранника, изображенного на рисунке, все плоские углы которого прямые, скрещивающиеся с прямой AB .
В режиме слайдов ответ появляется после кликанья мышкой
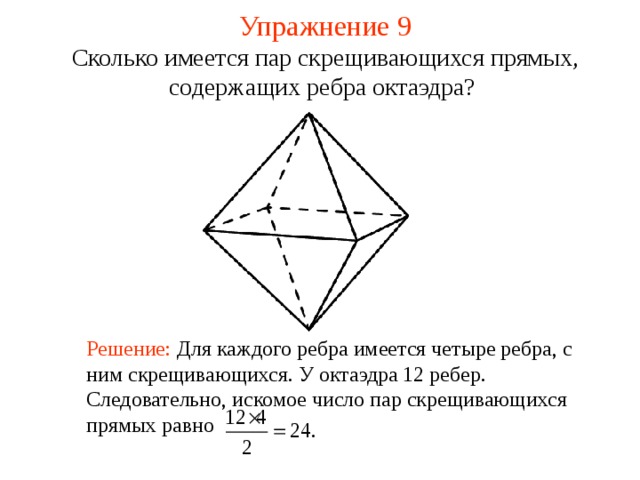
Сколько имеется пар скрещивающихся прямых, содержащих ребра октаэдра?
Решение: Для каждого ребра имеется четыре ребра, с ним скрещивающихся. У октаэдра 12 ребер. Следовательно, искомое число пар скрещивающихся прямых равно
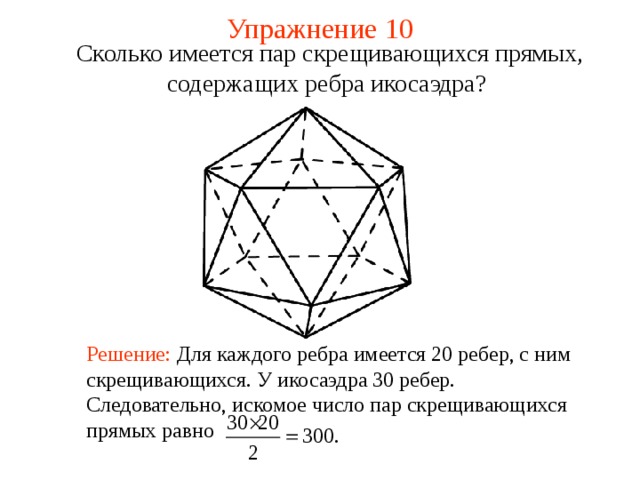
Сколько имеется пар скрещивающихся прямых, содержащих ребра икосаэдра?
Решение: Для каждого ребра имеется 20 ребер, с ним скрещивающихся. У икосаэдра 30 ребер. Следовательно, искомое число пар скрещивающихся прямых равно
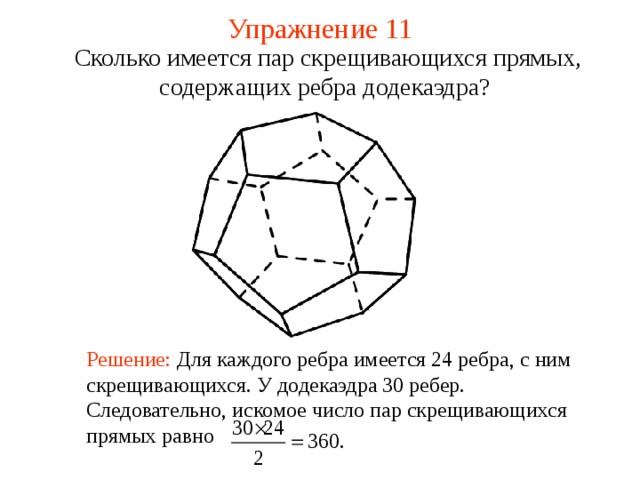
Сколько имеется пар скрещивающихся прямых, содержащих ребра додекаэдра?
Решение: Для каждого ребра имеется 24 ребра, с ним скрещивающихся. У додекаэдра 30 ребер. Следовательно, искомое число пар скрещивающихся прямых равно
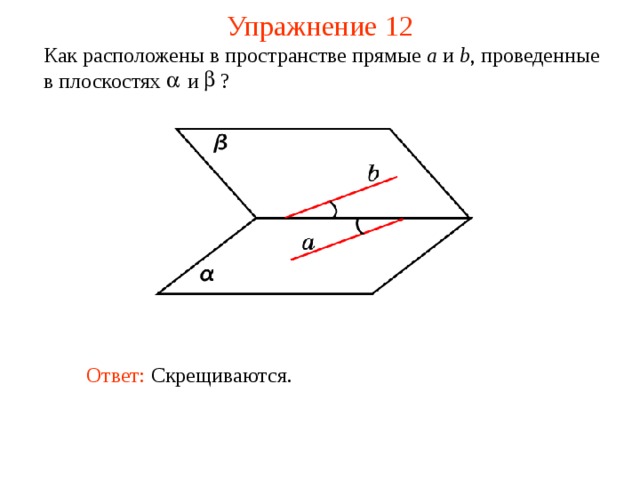
Как расположены в пространстве прямые a и b , проведенные в плоскостях и ?
Как в пространстве расположены прямые EF и GH , проведенные в плоскостях граней куба A … D 1 ?
Как в пространстве расположены прямые EF и GH , проведенные в плоскостях граней тетраэдра?
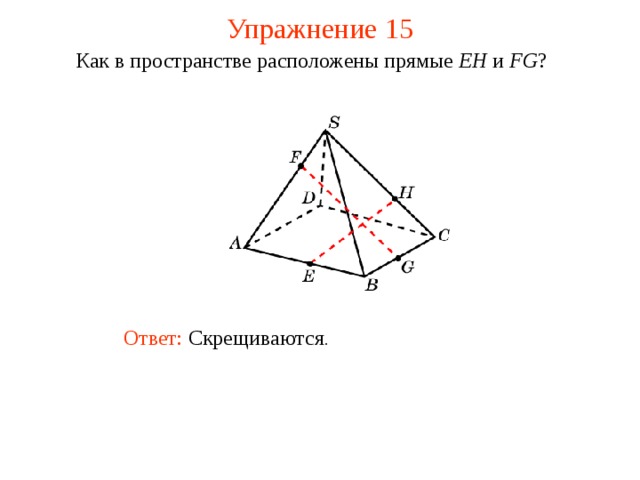
Как в пространстве расположены прямые EH и FG ?