- Формулы объема геометрических фигур
- Объем куба
- Объем призмы
- Объем параллелепипеда
- Объем прямоугольного параллелепипеда
- Объем пирамиды
- Объем правильного тетраэдра
- Объем цилиндра
- Объем конуса
- Объем шара
- Объемы фигур. Объем куба.
- Нахождение объема куба: формула и задачи
- Формула вычисления объема куба
- Примеры задач
- Таблица кубов и квадратов, как состовлять и найти
- Как появилось понятие куб числа?
- Степень с натуральным показателем
- Теория
- Возвести в куб онлайн
- Дополнительная информация
- Закон квадрата-куба
- Содержание
- Что чему пропорционально [ править ]
- Выводы [ править ]
- В биологии [ править ]
- В технике [ править ]
- Положительные стороны [ править ]
Формулы объема геометрических фигур
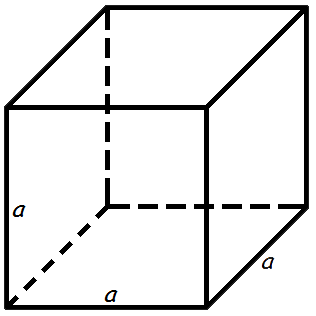
Объем куба
Объем куба равен кубу длины его грани.
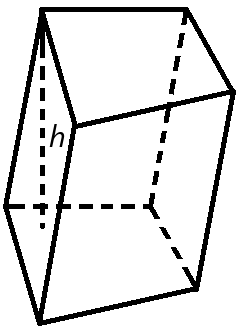
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
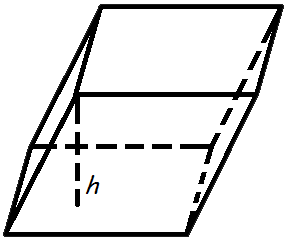
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
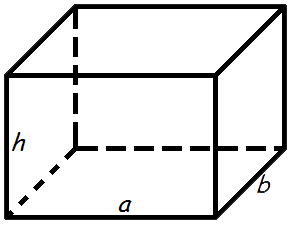
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
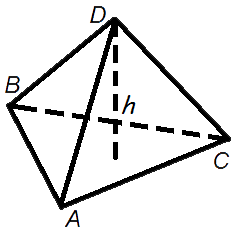
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
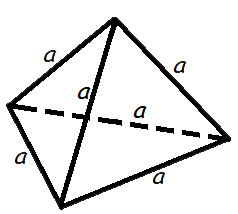
Объем правильного тетраэдра
Формула объема правильного тетраэдра:
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Объемы фигур. Объем куба.
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте).
У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны.
Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна
ширине и равна высоте, то объем куба равен s 3 ,
где s – длина одного (любого) ребра куба.

Воспользуйтесь онлайн калькулятором для расчета объема куба: объем куба, онлайн расчет.
Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.
Метод 1 из 3: Возведение в куб ребра куба
- Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы
вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.
Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.
Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза.
Если s — длина ребра куба, то
и, таким образом, вы вычислите объем куба.
Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на
ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть,
другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и
равна высоте, то это процесс можно заменить возведением ребра куба в третью степень.
В нашем примере объем куба равен:
- К ответу припишите единицы измерения объема. Так как объем – это количественная
характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические
В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических
сантиметрах (или в см 3 ). Итак, объем куба равен 125 см 3 .
Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих
Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м 3 .
Метод 2 из 3: Вычисление объема по площади поверхности
- В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых вы
можете найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите
ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем
возведите длину ребра куба в третью степень и вычислите объем куба.
Площадь поверхности куба равна 6s 2 ,
где s – длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так
как у куба 6 равных граней).
Рассмотрим пример. Площадь поверхности куба равна 50 см 2 . Найдите объем куба.
- Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь
одной грани куба). В свою очередь площадь одной грани куба равна s 2 , где s – длина ребра куба.
В нашем примере: 50/6 = 8,33 см 2 (не забывайте, что площадь измеряется в квадратных единицах — см 2 ,
- Так как площадь одной грани куба равна s 2 , то извлеките квадратный корень из значения площади
одной грани и получите длину ребра куба.
В нашем примере, √8,33 = 2,89 см.
- Возведите в куб полученное значение, чтобы найти объем куба.
В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см 3 . К ответу не забудьте приписать кубические
Метод 3 из 3: Вычисление объема по диагонали
- Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом,
если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив
Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба
равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см 3 .
где d — диагональ грани куба, s – ребро куба. Эта формула вытекает из теоремы Пифагора, согласно
которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен
сумме квадратов катетов (в нашем случае ребер), то есть:
- Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче
дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3.
Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный
(где D — диагональ куба, s – ребро куба).
Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае
диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет –
это ребро, а второй катет – это диагональ грани куба, равная 2s 2 ), то есть
Рассмотрим пример. Диагональ куба равна 10 м. Найдите объем куба.
Нахождение объема куба: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a 3
2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√ 2 .
Следовательно, вычислить объем куба можно так:
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .
Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
Таблица кубов и квадратов, как состовлять и найти
Как появилось понятие куб числа?
Древнегреческие математики оперировали так называемыми фигурными числами – числами, которые можно представить в виде фигуры. Выделялись, например:
Кубические числа выделялись в особый вид фигурных чисел, поскольку куб числа x равен объёму куба с длиной ребра, равной x .
Вообще, фигурные числа – интереснейшая тема . Ставьте лайки этому материалу, если хотите узнать о них больше!
Последовательность кубов натуральных чисел выглядит так
Полезно будет запомнить, хотя бы те, что меньше тысячи. Особенно мне нравится число 729. Посмотрите:
- 729 равно 9 в кубе;
- 729 равно 3 в шестой степени;
- 729 равно 27 в квадрате, что очень сильно нравилось пифагорейцам. Например, Платон считал, что количество ночей и дней в году равняется 729 (364, 5 на каждое время суток). Кроме того, он считал, что жизнь царя должна длиться 729 месяцев (около 67 лет).
Еще несколько интересных свойств кубов чисел:
- 1728 является количеством кубических дюймов в кубическом футе;
- 1728 – единственный композиториал , являющийся одновременно кубом числа. Композиториал – это факториал ( о нем я достаточно интересно уже писал ), деленный на праймориал – последовательность произведения простых чисел, меньше данного.
Вот так, к слову выглядит формула вычисления суммы первых кубов чисел:
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
Возвести число в куб — значит умножить его само на себя три раза.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Теория
Куб числа – это результат умножения числа само на себя три раза. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Данное выражение читается: «возвести в куб число 6» или «6 в кубе».
Возвести в куб онлайн
Как возвести число в куб онлайн!? Введите нужное число, которое требуется возвести в куб и нажмите возвести в куб. Справа от равно появится число, которое возвели в куб
Ну и далее пробежимся по нескольким поисковым запросам, которые так или иначе вы задаете в строке поиска!
Дополнительная информация
Квадратом числа называют произведение двух одинаковых множителей.
Мы уже пробовали находить квадраты первого десятка натуральных чисел.
Возводить двузначные числа, трехзначные и т.д. числа немного сложнее, главное хорошо знать и помнить таблицу умножения чисел.
Существует способ быстрого возведения в квадрат двухзначных чисел, которые оканчиваются на цифру 5.
1) Первую цифру числа, возводимого в квадрат, необходимо умножить на сумму этого числа и единицы.
2) Записать полученное число- это будут первые цифры ответа (с этих цифр начинается ответ).
3) Ответ всегда будет заканчиваться на 25 (т.е. в конце ответа всегда будет стоять число 25).
4) Приписываем к числу, полученному в п 2, число 25, получаем ответ.
Рассмотрим поясняющий пример.
Найдем квадрат 65.
65 2 = 65 ∙ 65
Первая цифра в числе 6 5– это цифра 6 , следовательно, нам необходимо найти произведение 6 и суммы 6 + 1.
6 ∙ (6 + 1) = 6 ∙ 7 = 42
Запишем число 42 и припишем к нему число 25.
Проверим: Так как квадрат числа- это произведение двух одинаковых множителей 65 2 = 65 ∙ 65, то
65 2 = 65 ∙ 65 = 4225
Получили все тот же ответ: 65 2 = 4225
Закон квадрата-куба
 | TV Tropes Для англоязычных и желающих ещё глубже ознакомиться с темой в проекте TV Tropes есть статья Square-Cube Law. Вы также можете помочь нашему проекту и перенести ценную информацию оттуда в эту статью. |
 | Вкратце Нельзя так просто взять и увеличить что-нибудь в 10 раз: площадь увеличится в 100 раз, объём в 1000 раз. |
| « | — Муравей может поднять вес, в 10 раз превышающий свой собственный. — Каждый может поднять вес в 10 раз больше муравья! | » |
| — ЧП и Зигзаг | ||
Закон квадрата-куба звучит так: если увеличить что-то в n раз, площадь поверхности увеличится в n² раз, объём — в n³ раз.
Одни параметры завязаны на объём (и увеличатся в n³ раз), другие — на площадь (и увеличатся всего лишь квадратично). Масса — n³, сила мышц — n², поэтому великан не сможет даже удержать себя. Так что простое увеличение или уменьшение знакомых вещей не работает, потребуется кардинальная переработка. И потому не бывает ОБЧР, гигантских насекомых, великанов и лилипутов, кайдзю, и т. д., и для этого по умолчанию необходимо вводить в сюжет магию, либо что-то ей подобное.
Содержание
Что чему пропорционально [ править ]
- Близка к константе (n 0 )
- Внезапно, скорость метания тел упругими конструкциями. И масса, и запасённая упругая энергия пропорциональна кубу размеров. С учетом ухода энергии во вращательное движение и некоторого снижения удельной прочности с увеличением размера — степень становится даже несколько отрицательной.
- Пропорционально корню линейного размера (n 0,5 )
- Скорость вытекания жидкости из сосуда.[1]
- Пропорционально линейному размеру (n)
- Давление на грунт, удельная нагрузка на конструкции.
- Толщина брони.
- Пропорционально площади (n²)
- Прочность конструкций, сила мускулов.
- Силы (в ньютонах! — не давление, которое в Н/м² = 1 Па ≈ 10 −5 атм) в тепловой, гидравлической или пневматической машине.
- Площадь опоры.
- Поверхность тела.
- Площадь и подъемная сила крыла.
- Сопротивление воздуха.
- Поверхность тепло- и газообмена.
- Пропускная способность труб.
- Вероятность попасть в объект хотя бы одним снарядом (если разброс больше, чем габариты объекта). Ну и за компанию — сколько шальных пуль и осколков примет на себя объект.
- Скорость обмена веществ организма (точнее, пропорциональна массе тела в степени 0,75).[2]
- Пропорционально объёму (n³)
- Масса и соответственно кинетическая энергия при той же скорости.
- Потребная мощность моторов.
- Сложность мозга и других информационных устройств.
- Пропорционально четвертой степени (n 4 )
- Момент инерционных сил, изламывающий момент.
- Пропорционально пятой степени (n 5 )
- Момент инерции — аналог массы для вращательного движения. В одиночестве не используется, но сильно мешает быстро раскручивать-тормозить вращение всякого большого хлама.
- Центробежные силы при постоянной частоте вращения — масса эксцентрика пропорциональна кубу, а ускорение — квадрату размера.
Выводы [ править ]
В биологии [ править ]
Насекомые очень малы (n малó), и у них отношение поверхности газообмена к массе (n²/n³ = 1/n) большое. Так что нечего природе и огород городить, насекомым достаточно дышать простой диффузией (т. н. трахеями). А нам приходится принудительно прокачивать воздух через дыхательные пути. И лапки у насекомых тонюсенькие относительно всего тела. Знаете такую шутку: «По законам аэродинамики шмель летать не может, но он этого не знает и летает»? По самолётным формулам для самолётных масштабов — да. А шмелю помогает закон квадрата-куба: размер крыльев и управляющих поверхностей нужен совсем небольшой. И с малыми размерами возможны совсем другие принципы полёта, разгаданные только в последние десятилетия.
Почему кузнечик прыгает на полметра, а слон не прыгает вообще? Потому что масса (и ударные нагрузки от прыжков) n³, а прочность костей и сила ног всего лишь n². А ещё насекомое может упасть практически с любой высоты: большой запас прочности и большое сопротивление воздуха (относительно массы, разумеется) не дадут разбиться.
Это же делает Человека-паука невозможным в мире с нашими законами физики.
Что, одни плюсы от малого размера? А минусы в том, что отношение поверхности теплообмена к массе — те же 1/n. Другими словами, маленький не может быть теплокровным. Замечали, как в августе колорадские жуки становятся квёлыми? А температура упала всего чуть-чуть. А сложность мозга уменьшается кубически — n³ — так что и разумным тоже не станешь. И кинетическая энергия n³ — препятствия, непроходимые для мелких существ, крупные с лёгкостью сносят.
Расчеты, сделанные но основании изучения системы дыхания акул, позволили сделать вывод, что максимально возможный предел в их размерах составляет около 15 метров. Поскольку при увеличении размеров тела поверхность жабер увеличивается непропорционально, это не позволяет доставить требуемое количество кислорода в организм. Указанная цифра примерно соотносится с размерами крупнейших достоверно измеренных китовых и гигантских акул, а также теоретическими прикидками относительно предельных размеров вымершего мегалодона.
В технике [ править ]
Почему для небоскрёбов потребовались прочные сорта стали? Потому что прочность всего лишь n², а масса n³. Так что при увеличении размера постройки в n раз удельная нагрузка на конструкции повысится в те же n раз.
Гигантские самолёты («Мрия», A380) непривычны для наших глаз именно из-за непропорциональных размеров крыльев и управляющих поверхностей: их приходится делать в √ n раз больше, чем нужно было бы при пропорциональном увеличении. А дирижабли можно делать гигантскими, и они сохранят те же пропорции: подъёмная сила их баллонов зависит от объёма, а не от площади, и растет в ногу с массой дирижабля.
- В некотором смысле большие дирижабли даже удобнее — в маленьких обшивка достаточной прочности будет слишком толста по сравнению с размерами дирижабля. Крошечные коптеры вполне существуют, а вот крошечных дирижаблей — нет. Но ветровое воздействие хуже переносится именно большими.
- что показывает только одно — масштабирование конструкции в любую сторону простым увеличением всех линейных размеров применимо крайне ограничено. При желании, большой цепеллин можно сделать хоть в форме клина или гигантского летающего крыла, хоть любой иной формы, если она будет лучше держать нагрузки.
Если увеличить мотор в n раз, давление в нём не изменится, площадь поршней увеличится в n² раз, масса деталей в n³ раз — другими словами, обороты мотора уменьшатся в n раз, а мощность — увеличится в n² раз. Замечали, как тихоходны огромные судовые двигатели? Кроме того, одни детали будут работать с увеличенными нагрузками, другие с уменьшенными — поэтому потребуется переработка всего, что есть в моторе. Тоньше картер, слабее поршни, это потребует более лёгких противовесов… А можно, наоборот, форсировать двигатель, уменьшив сами цилиндры, но увеличив их количество и усилив систему охлаждения (не забыли, её эффективность n²?) А ещё придётся переделать капот той машины, в которой этот мотор будет стоять.
- Вышесказанное справедливо для теплового двигателя, а как закон квадрата-куба отразится на электрическом двигателе или электрическом генераторе?
- Магнитное поле с размером не меняется, движущая сила — пропорционально плотности тока в обмотке на куб её размера, момент — плотности тока на четвёртую степень размеров. Мощность — четвертая степень размера на плотность тока и частоту вращения. Но момент инерции пропорционален пятой степени, так что разгоняться он будет медленнее. Проблемы с нагревом с увеличением размеров усиливаются, так что придётся снижать плотность тока, или городить более сложную и эффективную систему охлаждения, благо это становится проще.
- В 50х любили развлекаться с электростатическими генераторами, что повлекло за собой внимание к этому делу Ландау, который объяснил идиотам, что дабы получить промышленную мощность, скажем, для завода, генератор придется строить размером с гору. Публика сделала выводы.
- Усилия в подшипниках возрастают как куб/пятая (от центробежных сил) степень, а их прочность — как квадрат. Так что сильно размеры не поднять.
- Магнитное поле с размером не меняется, движущая сила — пропорционально плотности тока в обмотке на куб её размера, момент — плотности тока на четвёртую степень размеров. Мощность — четвертая степень размера на плотность тока и частоту вращения. Но момент инерции пропорционален пятой степени, так что разгоняться он будет медленнее. Проблемы с нагревом с увеличением размеров усиливаются, так что придётся снижать плотность тока, или городить более сложную и эффективную систему охлаждения, благо это становится проще.
В авиации есть изящный термин «уравнение существования». Это эмпирический закон, показывающий приблизительную составляющую долю в общей массе всех узлов, образующих самолет, чтобы он мог летать. Для более крупного самолета нужен более мощный двигатель. Этот двигатель будет чуть тяжелее, поэтому понадобится более крупное крыло. Это крыло тоже будет чуть тяжелее, поэтому эта «гонка весов» асимптотически стремится к… …новому самолету, в котором двигатели по прежнему будут занимать, скажем, 35 % веса, но общая масса самолета возрастет раза в два. Например И-16 при мощности двигателя около 1000 лошадиных сил имел взлётную массу 1800—1900 кг, а его прямой потомок И-185 с 2000-сильным двигателем тянул уже на 3800. В общем случае это тот же ракетный закон — считается что полезная нагрузка примерно равна 1 % массы ракеты (разумеется это сильное упрощение, однако «протон» при массе около 700 тонн на геопереходную орбиту вытаскивает около 7 тонн, так что для примера покатит, логичнее было бы говорить об отношении полезной нагрузки к сухой массе ракеты), важно не это, а то что принцип «топливо которое тащит топливо» порождает ту же проблему что и у самолётостроителей. Нельзя просто отмасштабировать, нужно делать новую ракету с нуля. Костыли в виде модульности, «летающего забора» и аспарагуса дело лишь усугубляют, ибо относятся к удешевлению и стандартизации, а не к увеличению эффективности конструкции.
- Энергия пули — (mv²)/2, импульс — mv. По закону сохранения импульса ружьё летит назад во столько раз медленнее, во сколько раз оно тяжелее пули. Но при этом кинетическая энергия, которая достанется плечу стрелка, во столько же раз меньше кинетической энергии пули, т. к. она пропорциональна квадрату скорости и всего лишь первой степени от массы. По мере увеличения калибра и приближения массы поражающего элемента к массе оружия ситуация всё больше напоминает одновременный выстрел в утку и себе в плечо, со всеми сопутствующими переломами ключиц.
Положительные стороны [ править ]
Объём топлива и перевозимого груза на корабле растёт пропорционально кубу, а сечение, которое надо пропихивать через воду — квадрату. Поэтому суда всё монструознее и монструознее.
- Если речь идёт о гребных судах, то увеличение судна в длину с добавлением дополнительных гребцов увеличивает только трение бортов о воду, которое составляет меньшую долю в общем сопротивлении воды, но оставляет неизменным вышеупомянутое сечение, пропихивание которого и создаёт основную проблему — мощность растёт линейно (точнее, медленнее, чем линейно, но быстрее, чем с показателем 1/2), затраты — значительно медленнее. А учитывая, что длинная лодка создаёт меньшую турбулентность в воде, чем короткая, получается именно так: чем длиннее лодка и больше на ней гребцов — тем эффективнее вся конструкция. Дальше всё упирается только в прочность, где закон квадрата-куба превращается просто в закон квадрата: при простом удлинении лодки нагрузка на корпус в средней части растёт квадратично (именно поэтому деревянные галеры, а позже — линкоры ломались пополам), а его прочность не изменяется вообще.
- Правда, остается ещё волновое сопротивление.
- особо борзые конструкторы решили положить на данный закон с прибором с помощью «смазки». Для подводных судов — кавитационный пузырь (это позволило гонять под водой как и не снилось, правда шума было много), для воздушных — плазменная (нормально сделать не смогли, потому как плазма сильно мешает ориентироваться в пространстве, плюс сейчас скорости явно не те). Что, в принципе, логично. Кстати авторам фантастики на заметку, что шайхулудам необходимо превращать землю в грязь дабы очень быстро в ней двигаться.
- Корабли вообще, и особенно военные в частности. Здоровенные подлодки проекта «Акула» добрые люди прозвали водовозами за то, что в норме, половину массы судна составляет балластная (!) вода. То ли резерва плавучести на случай повреждения, то ли просто не смогли придумать, что ЕЩЁ впихнуть в этот гигантский объем.
- Другой пример — линкоры. Если проследить их историю, то с увеличением водоизмещения вырастала и толщина брони. В итоге, знаменитый «Ямато» в самых толстых местах имел полметра брони. Если бы она ещё была нормального качества, а в составе эскадры оставались авианосцы для прикрытия этой туши. А так, только анекдот про три самые бесполезные на свете вещи — Египетские пирамиды, Великую Китайскую Стены, и сабж.
То же с дирижаблями: масса оболочки при равной толщине растёт по квадрату, рабочий объем — по кубу, да и аэродинамика улучшается, как у судов. А керосин всё дороже, и перспективы возрождения воздухоплавания всё заманчивее. Правда автор сего тезиса почему-то думает что дирижабли подобны воздушным шарам. Нихрена — тепловые дирижабли помимо топлива чтобы ворочать конструкцию, нуждаются ещё и в подогреве рабочего тела. А теперь мякотка: автор примечания как-то в споре с коллегами проводил примерный расчет дирижабля Циолковского, после чего всякое желание строить монструозную хренотень способную засунуть в трюм пару-тройку супертанкеров пропало напрочь: парусность сего такова, что никаких двигателей не хватит чтобы ей нормально управлять или хоть как-то двигать, а уж чтоб просто взлетела (это тепловой дирижабль) потребуются тысячи тонн топлива. Циолковский, правда, считал, что оно само взлетит (солнце нагреет газ), но похоже, нет. С двигательной установкой тоже всё печально — как и в случае с океанскими лайнерами (где на увеличение скорости в 1 узел приходилось удваивать мощность силовой установки, что привело к эпическим 500 000 л.с. у лайнера способного жать 35 узлов), дабы сдвинуть с места воздушное судно в несколько сот тысяч тонн, более-менее годится только реактивный двигатель, причем здоровенный, жрущий топливо как не в себя, в итоге дирижабль больше похож на ракету, прицепленную к воздушному шарику — тяга нивелируется драгой. То есть летает медленно, управляется плохо, топлива жрёт много, вывод — нерентабельно, если конечно вам не надо тащить что-то охрененно здоровое и нетранспортабельное туда куда иным способом это притащить нельзя. Однако проведение ОКР (опытно-конструкторских работ) в этой области способно обогатить инженерию решениями, которые могут позже пригодиться — для воздушных космодромов, удешевляющих запуски, или для баз в атмосфере Венеры, или ещё зачем-нибудь.