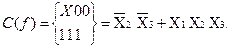Построение комплекса кубов и его минимального покрытия
Терм максимального ранга n- куба принято называть 0-кубом (точка вершины) и обозначают К 0 . Например, для f(x1,x2,x3)= (0,4,7) комплекс 0-кубов будет таким
Определение. Если два 0-куба из комплекса К 0 различаются только по одной координате, то два таких 0-куба образуют один 1-куб. Он представляется общими элементами 0-кубов, причем на месте координаты, по которой различаются 0-кубы, указывают символ Х, обозначающий независимую координату (переменную). Различие координат определяют последовательным сравнением первого куба с остальными, затем второго с остальными и так далее. Например, два 0-куба 000 и 100 различаются только по одной координате, и они образуют 1-куб (отрезок), которому соответствует ребро трехмерного куба. Заметим, что 0-куб 111 не склеивается, так как отличается больше чем по одной координате.
Все множество 1-кубов функции называется кубическим комплексом К- один и обозначается- К 1 .
Комплекс К 1 строится по комплексу К 0 путем их сравнения и определяет все множество ребер, на концах которых функция принимает единичные значения. Если два 1-куба из комплекса К 1 имеют общую независимую компоненту и различаются только по одной координате, то они образуют один 2-куб. Это грань для трехмерного куба. Все множество 2-кубов, построенного из комплекса К 1 , образует множество комплекса К 2 (множество граней). Комплекс К 3 = 0 — отсутствует в трехмерном кубе (часто r-куб называют интервалом (расстоянием) r- порядка). Перед построением очередного куба необходимо отметить те кубы, которые склеились хотя бы один раз. Например, звездочкой *. Это необходимо, так как могут быть неотмеченные (не склеившиеся) кубы о которых забывать нельзя. Они являются самостоятельными импликантами, которые так же включают в общее покрытие кубов С(f). Для нашего примера, общее покрытие будет выглядеть
По индукции можно определить, что два r-куба, содержащие r координат и различающиеся только по одной координате, могут объединяться в (r + 1)-куб, (r + 1)-я независимая координата которого соответствует координате, по которой различаются r-кубы.
Запись (r + 1)-куба состоит из общих компонент двух r-кубов, а компонента, принимающая в них различные значения, обозначается в (r + 1)-кубе как независимая компонента Х.
Число независимых координат Х в кубе определяет его размерность.
Например, куб 0Х1Х1ХХ имеет размерность r = 4.
Определение. Объединение кубов комплексов К 0 ,К 1 . К n функции f(x1, x2, …, хn) называется кубическим комплексом K(f) функции f.
K(f) = K(f) = К 0 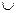
В отличие от аналитических форм записи булевых функций, кубическое представление позволяет задавать булевы функции в виде множества кубов, компонентами которых являются только три символа 0; 1; X. Ограниченное количество символов в записи функций алгебры логики позволяет автоматизировать процесс минимизации с применением компьютерных систем.
Задача минимизации булевых функций по критерию минимальности числа букв входящих в ДНФ или КНФ называется канонической задачей минимизации.
Схема, получаемая в результате ее решения не является абсолютно минимальной, т.к. абсолютный минимум оборудования в большинстве случаев так и не достигается.
Определение. Булева функция f(x1, x2, …, хn) представляется как множество С кубов, принадлежащих комплексу К(f), и таких, что каждая вершина комплекса К 0 включена по крайней мере в один куб множества С.
Полученное таким образом множество С называется покрытием комплекса K(f) и покрытием булевой функции. Каждому покрытию C(f) соответствует ДНФ функции.
f(х)= (3,4,5,6,7)= 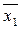
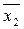
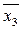
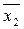
Построим комплекс кубов К 0 ,К 1 ,К 2 ,К 3 .



Из комплекса кубов K(f) определяется его покрытие C(f) куда входят не отмеченная импликанта Х11 из куба К 1 и покрытие 1ХХ из куба К 2 .
C(f) = 
Это покрытие включает в себя все 5 вершин комплекса К°. В самом деле, куб x11 может включать (покрывать) 011; 111. Куб 1xx может включать вершины 100, 101, 110, 111. Таким образом, множество C(f) является покрытием комплекса K(f). Отсюда можно написать минимизированное уравнение:
Метод Квайна-Мак-Класски
При минимизации по методу Квайна предполагается, что минимизируемая функция представленна в СДНФ.
Метод Квайна состоит из последовательного выполнения нескольких этапов.
1-й этап. Нахождение первичных импликант.
Все минтермы данной функции сравниваются попарно. Если минтермы отличаются одной координатой типа Fхi+F 
Другими словами, нахождение простых импликант сводится к построению комплекса кубов
K(f) = К 0 
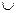
При построении последующих кубов, образующие предыдущие кубы отмечаются, чтобы выявить неотмеченные кубы.
Этап заканчивается, когда ни один (r+1)-куб не может быть построен. При этом, все неотмеченные кубы комплекса K(f) тоже являются простыми импликантами и входят в покрытие C(f) функции f.
Пример. Пусть задана функция
Для упрощения, 0-кубы упорядочивают по числу 1-ых координат (см. рисунок 6.3).
Простые и неотмеченные импликанты образуют покрытие С(f), которое может быть избыточным и требует последующих этапов минимизации, а именно — составления таблиц покрытия функции.
2-й этап. Составление таблиц покрытий.
Понятно, что для нахождения минимальной формы покрытия необходимо удалить из покрытия некоторые простые или неотмеченные импликанты. Для этого используют таблицу, строки которой составляют импликанты покрытия, а столбцы — 0-кубы (минтермы) исходной функции. Если импликанта отличается от 0-куба (кроме независимых координат), то на их пересечении не ставится метка + (см. таблицу 6.1).
Таблица 6.1-Таблица покрытий комплекса кубов
| Вершины 0-кубов | ||||||||||||||
| Импликанты | ||||||||||||||
| X00XX 00X0X X0X01 10XX1 1X111 | + + | + ++ | + | + | + | + | ++ | + ++ | + | ++ | + + | + + | ++ | + |
3-й этап. Определение существенных импликант.
Если в столбце таблицы покрытий имеется только одна метка, то первичная импликанта, стоящая в соответствующей строке, является существенной импликантой, и ее выписывают в новое минимальное покрытие C(f). Из таблицы покрытий исключаются строки, соответствующие существенным импликантам и столбцы минтермов, покрываемым этими существенными импликантами. Покрытие будет иметь вид :
C(f) = 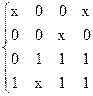

В результате упрощения, получим новую таблицу 6.2
4-й этап. Вычеркивание лишних столбцов.
Если в таблице существенных импликант есть два столбца имеющих метки в одинаковых строках, то один из столбцов вычеркивается.
5-й этап. Вычеркивание простых лишних импликант.
Если после вычеркивания столбцов в таблице появляются строки без меток, то импликанты этих строк вычеркиваются.
6-й этап. Выбор минимального покрытия.
В таблице, полученной после выделения существенных импликант, выбирается совокупность простых импликант, обеспечивающая покрытие всех столбцов с минимальной ценой С A .
В нашем примере выбирается импликанта Х0Х01 ( или 10ХХ1, т.к. цены С A одинаковы).
Таким образом, покрытие функции имеет вид:
С(f) = 
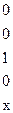

и определяет минимальную ДНФ
f = 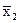
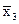

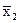




При использовании метода Квайна для СКНФ необходимо рассматривать значения функций f=0 и макстермы, соответствующие этим значениям. В результате получим
Далее необходимо воспользоваться соотношением де — Моргана с тем, чтобы привести функцию к СДНФ. Все дальнейшие действия аналогичны.
Покрытия булевых функций .
Между кубами различной размерности, входящих в кубический комплекс K(f), существует отношение включения или покрытия. Принято говорить, что куб А меньшей размерности покрывается кубом Б большей размерности, если куб А включается в куб Б. Это означает, что при образовании куба Б хотя бы в одном склеивании учавствует куб А.
Отношение включения (покрытия) между кубами принято обозначать АÌБ. В теории множеств отношение включения связывает между собой некоторое множество и его подмножества.
Для рассмотренного примера отношения включения имеют место между 001Ì0х1; 011Ìx11Ìx1x. любой 1-куб покрывает 2 0-куба, 2-куб — 4 0-куба и 2 1-куба, 3-куб покрывает 8 0-кубов, 12 1-кубов и 6 2-кубов.
Покрытием булевой функции f называется такое подмножество кубов из кубического комплекса K(f), которое покрывает все существенные вершины функции.
В связи с тем, что любому кубу комплекса K(f) можно поставить в соответствие конъюнктивный терм, для любого покрытия можно представить некоторую ДНФ булевой функции.
Частным случаем покрытия булевой функции является кубический комплекс K 0 (f), покрытие c 0 (f)=K 0 (f). Этому покрытию соответствует КДНФ.
Для примера покрытием является также
этому покрытию соответствует ДНФ вида
В качестве минимальной еще одного покрытия можно использовать множество максимальных кубов
Действительно, куб 0х1 покрывает существенные вершины 0х1É(001, 011), а куб x1xÉ(010, 011, 110, 111).
Множество максимальных кубов булевой функции всегда является ее покрытием.
Покрытие c 2 (f) соответствует ДНФ вида х1х3vx2. Эта ДНФ является минимальной. Покрытие булевой функции, которое соответствует минимальной ДНФ называется минимальным покрытием.
Минимальное покрытие должно состоять только из максимальных кубов.
В частном случае все множество максимальных кубов является минимальным покрытием. Это справедливо для нашего примера. В общем случае множество максимальных кубов является избыточным и для получения минимального покрытия достаточно взять некоторое его подмножество.
Для данного примера множество максимальных кубов совпадает с комплексом K 1 (f). Z(f)=K 1 (f)
Минимальными покрытиями являются
Из анализа покрытия существенных вершин максимальными кубами из комплекса K 1 (f) следует :
1) Куб 00х должен обязательно включаться в покрытие, так как только он покрывает существенную вершину 001, аналогично 11х покрывает 111.
Множество максимальных кубов без которых не может быть образовано покрытие булевой функции называется ядром покрытия T(f)=|00x
2) Так как ядром покрытия кроме существенных вершин 001 и 111 покрываются также существенные вершины 000 и 110, то не покрытой ядром остается только существенная вершина 100. Для ее покрытия достаточно взять 1 из оставшихся максимальных кубов (х00 или 1х0).
Задача получения минимальной ДНФ сводится к задаче получения минимального покрытия.
Получение минимального покрытия реализуется в таком порядке : а) Находится множество максимальных кубов б) Выделяется ядро покрытия в) Из максимальных кубов, не вошедших в ядро, выбирается такое минимальное подмножество, которое покрывает существенные вершины, не покрытые ядром.
Цена покрытия .
Цена r-куба представляет собой количество несвязанных координат. Sr=n*r
Для оценки качества покрытия используют два вида цены покрытия :
1) S a =åSrNr, где Nr — количество r-кубов, входящих в по-
крытие, m — максимальная размерность куба. Цена S a представляет собой сумму цен кубов, входящих в покрытие.
2) S b =S a +k, где k — количество кубов, входящих в покрытие
Под минимальным покрытием понимают покрытие, обладающее минимальной ценой S a по сравнению с любым другим покрытием этой функции.
Можно показать, что покрытие, обладающее минимальной ценой S a обладает также и минимальной ценой S b .
C 0 (f)=K 0 (f) ; S a =5*3=15 ; S b =S a +5=20
C 1 (f)=K 1 (f) ; S a =4*2=8 ; S b =S a +4=12
Цена покрытия S a представляет собой количество букв, входящих в ДНФ, которая соответствует данному покрытию.
Цена S b представляет для ДНФ сумму количества букв и количества термов.
Цена покрытия хорошо согласуется с ценой схемы по Квайну, которая строится по нормальной форме, соответствующей этому покрытию.
Для приведенной схемы цена по Квайну SQ=9=S b (9-число входов).
В принципе, между SQ и ценами S a и S b существует соотношение S a £ SQ £ S b Это неравенство имеет место при следующих допущениях по комбинационной схеме :
1) Схема строится по нормальной форме (ДНФ или КНФ).
2) Схема строится на элементах булевого базиса (И, ИЛИ).
3) На входы схемы можно подавать как прямые, так и инверсные значения входных переменных, представляющие собой значения аргументов булевой функции (схема с парафазными входами). Элементы НЕ (инвертора в схеме отсутствуют.