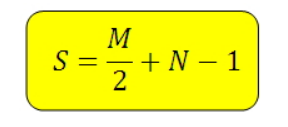Является ли частным случаем цилиндра куб прямоугольный параллелепипед

Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.

Источник

№ 496. ГДЗ Математика 5 класс Никольский. Помогите ответить про куб.

а) Что называют кубом?
б) Является ли любой прямоугольный параллелепипед кубом?

а) Прямоугольный параллелепипед, у которого все ребра равны.
б) Любой куб является прямоугольным параллелепипедом, обратное
неверно.

370.
На прямой даны три точки Л, Я и С, причём АВ= 13см, АС = 4 см. Найдите длину отрезка ВС. (Задача имеет два решения.)

Перевозки между населёнными пунктами А, В, С, D, Е осуществляют три компании, представившие стоимость свои услуг в табличной форме. ( Подробнее. )

В приведённых ниже предложениях из прочитанного текста пронумерованы все запятые. Выпишите цифры, обозначающие запятые при вводной ( Подробнее. )

Источник

Многогранники: призма, параллелепипед, куб

Определение

Многогранником будем называть замкнутую поверхность, составленную из многоугольников и ограничивающую некоторую часть пространства.

Отрезки, являющиеся сторонами этих многоугольников, называются ребрами многогранника, а сами многоугольники – гранями. Вершины многоугольников называются вершинами многогранника.

Будем рассматривать только выпуклые многогранники (это такой многогранник, который находится по одну сторону от каждой плоскости, содержащей его грань).

Многоугольники, из которых составлен многогранник, образуют его поверхность. Часть пространства, которую ограничивает данный многогранник, называется его внутренностью.

Определение: призма

Рассмотрим два равных многоугольника \(A_1A_2A_3. A_n\) и \(B_1B_2B_3. B_n\) , находящихся в параллельных плоскостях так, что отрезки \(A_1B_1, \ A_2B_2, . A_nB_n\) параллельны. Многогранник, образованный многоугольниками \(A_1A_2A_3. A_n\) и \(B_1B_2B_3. B_n\) , а также параллелограммами \(A_1B_1B_2A_2, \ A_2B_2B_3A_3, . \) , называется ( \(n\) -угольной) призмой.

Многоугольники \(A_1A_2A_3. A_n\) и \(B_1B_2B_3. B_n\) называются основаниями призмы, параллелограммы \(A_1B_1B_2A_2, \ A_2B_2B_3A_3, . \) – боковыми гранями, отрезки \(A_1B_1, \ A_2B_2, \ . A_nB_n\) – боковыми ребрами.
Таким образом, боковые ребра призмы параллельны и равны между собой.

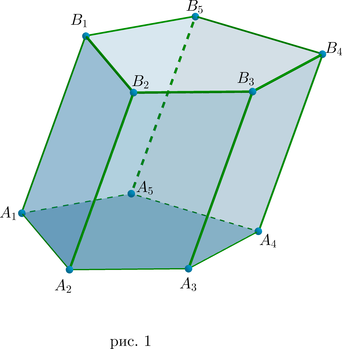
Рассмотрим пример — призма \(A_1A_2A_3A_4A_5B_1B_2B_3B_4B_5\) , в основании которой лежит выпуклый пятиугольник.

Высота призмы – это перпендикуляр, опущенный из любой точки одного основания к плоскости другого основания.

Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (рис. 1), в противном случае – прямой. У прямой призмы боковые ребра являются высотами, а боковые грани – равными прямоугольниками.

Если в основании прямой призмы лежит правильный многоугольник, то призма называется правильной.

Определение: понятие объема

Единица измерения объема – единичный куб (куб размерами \(1\times1\times1\) ед \(^3\) , где ед — некоторая единица измерения).

Можно сказать, что объем многогранника – это величина пространства, которую ограничивает этот многогранник. Иначе: это величина, числовое значение которой показывает, сколько раз единичный куб и его части вмещаются в данный многогранник.

Объем имеет те же свойства, что и площадь:

1. Объемы равных фигур равны.

2. Если многогранник составлен из нескольких непересекающихся многогранников, то его объем равен сумме объемов этих многогранников.

3. Объем – величина неотрицательная.

4. Объем измеряется в см \(^3\) (кубические сантиметры), м \(^3\) (кубические метры) и т.д.

1. Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.
Площадь боковой поверхности — сумма площадей боковых граней призмы.

2. Объем призмы равен произведению площади основания на высоту призмы: \[V_<\text<призмы>>=S_<\text<осн>>\cdot h\]

Определение: параллелепипед

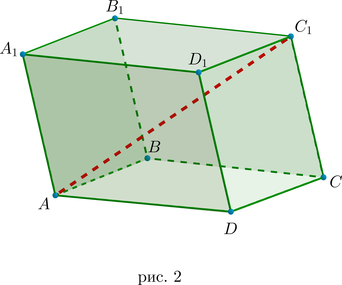
Параллелепипед – это призма, в основании которой лежит параллелограмм.

Все грани параллелепипеда (их \(6\) : \(4\) боковые грани и \(2\) основания) представляют собой параллелограммы, причем противоположные грани (параллельные друг другу) представляют собой равные параллелограммы (рис. 2).

Диагональ параллелепипеда – это отрезок, соединяющий две вершины параллелепипеда, не лежащие в одной грани (их \(8\) : \(AC_1, \ A_1C, \ BD_1, \ B_1D\) и т.д.).

Прямоугольный параллелепипед — это прямой параллелепипед, в основании которого лежит прямоугольник.
Т.к. это прямой параллелепипед, то боковые грани представляют собой прямоугольники. Значит, вообще все грани прямоугольного параллелепипеда – прямоугольники.

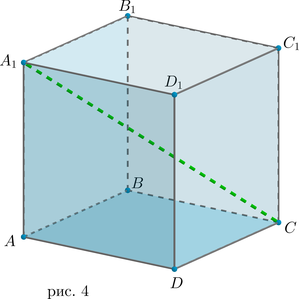
Все диагонали прямоугольного параллелепипеда равны (это следует из равенства треугольников \(\triangle ACC_1=\triangle AA_1C=\triangle BDD_1=\triangle BB_1D\) и т.д.).

Таким образом, параллелепипед обладает всеми свойствами призмы.

Площадь боковой поверхности прямоугольного параллелепипеда равна \[S_<\text<боков.пов-ти прямоуг. пар-да>>=2(a+b)c\]

Площадь полной поверхности прямоугольного параллелепипеда равна \[S_<\text<полн.пов-ти прямоуг. пар-да>>=2(ab+ac+bc)\]

Объем прямоугольного параллелепипеда равен произведению трех его ребер, выходящих из одной вершины (три измерения прямоугольного параллелепипеда): \[V_<\text<прямоуг.пар-да>>=abc\]

Доказательство

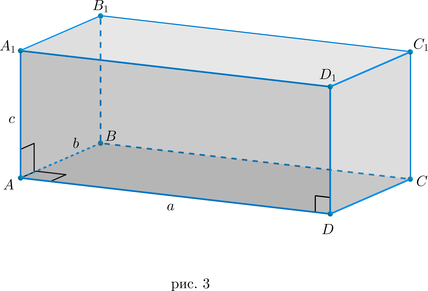
Т.к. у прямоугольного параллелепипеда боковые ребра перпендикулярны основанию, то они являются и его высотами, то есть \(h=AA_1=c\) Т.к. в основании лежит прямоугольник, то \(S_<\text<осн>>=AB\cdot AD=ab\) . Отсюда и следует данная формула.

Диагональ \(d\) прямоугольного параллелепипеда ищется по формуле (где \(a,b,c\) — измерения параллелепипеда) \[d^2=a^2+b^2+c^2\]

Доказательство

Рассмотрим рис. 3. Т.к. в основании лежит прямоугольник, то \(\triangle ABD\) – прямоугольный, следовательно, по теореме Пифагора \(BD^2=AB^2+AD^2=a^2+b^2\) .

Т.к. все боковые ребра перпендикулярны основаниям, то \(BB_1\perp (ABC) \Rightarrow BB_1\) перпендикулярно любой прямой в этой плоскости, т.е. \(BB_1\perp BD\) . Значит, \(\triangle BB_1D\) – прямоугольный. Тогда по теореме Пифагора \(B_1D=BB_1^2+BD^2=a^2+b^2+c^2\) , чтд.

Определение: куб

Куб — это прямоугольный параллелепипед, все грани которого – равные квадраты.

Таким образом, три измерения равны между собой: \(a=b=c\) . Значит, верны следующие

1. Объем куба с ребром \(a\) равен \(V_<\text<куба>>=a^3\) .

2. Диагональ куба ищется по формуле \(d=a\sqrt3\) .

3. Площадь полной поверхности куба \(S_<\text<полн.пов-ти куба>>=6a^2\) .

Источник

Является ли куб прямоугольным параллелепипедом?

Конечно да! Потому что у прямоугольного параллелепипеда все грани прямоугольники, а грань куба — прямоугольник, т.е. квадрат, правда не все кубы могут быть прямоугольными)

Да, является, как частный случай прямоугольного параллелепипеда в равными ребрами.

Куб, разумеется, является прямоугольным параллелепипедом. Это связано с тем, что квадрат, который является основанием данной геометрической фигуры, есть частный случай прямоугольника и параллелограмма.

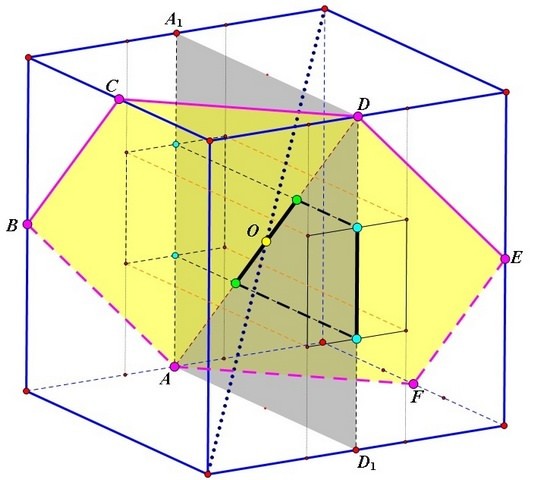
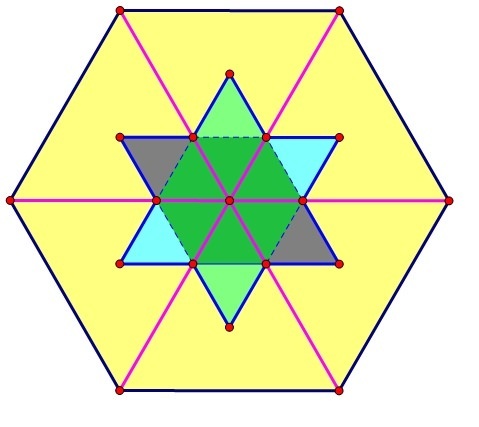
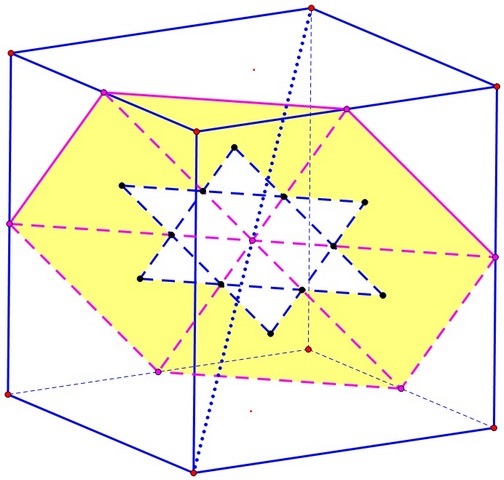
Проходя через куб плоскость сечения образует шестиугольник.

Отдельно взятое сквозное отверстие вырезает в плоскости данного сечения ромб, стороны которого параллельны диагоналям полученного шестиугольника.

Ромбы от трех сквозных отверстий, налаживаясь друг на друга, образуют собой звезду Давида.

В объёме это будет выглядеть так:

Правильный ответ: Г)

Сперва давайте вспомним, что же такое двугранный угол. Это просто угол между двумя плоскостями, или быть совсем точной, между двумя полуплоскостями. Плоскости в случае параллелепипеда — это его грани и они пересекаются по ребрам параллелепипеда. Измеряют двугранный угол проведением перпендикуляров к прямой пересечения плоскостей, то есть в нашем случае — к ребрам. Поскольку перпендикуляр можно провести к любой точке лежащей на ребре, то по сути все ребро — это место расположения вершин углов образованных этими перпендикулярами, иначе говоря — двугранный угол. Посчитаем сколько ребер имеет параллелепипед — это и будет число двугранных углов. Их в параллелепипеде 12.

В четырехугольнике может быть три тупых угла. Начертите квадрат АВСD. Представьте, что вершины это четыре иголки, воткнутые в пластину, а стороны сделаны из резины. Теперь приподнимите Вершину (иголку) D, и оттяните ей резинку подальше от центра. Если увести ее бесконечно далеко, то угол D будет стремиться к нулю, а углы С и А к 135 градусам. А теперь, чуть-чуть отведите подальше от центра квадрата вершины А и С. Тогда угол В станет чуть больше 90 градусов, т.е. он тупой. Углы А и С будут чуть меньше 135 градусов, т.е тоже тупые, а угол D будет очень малым. Итак три тупых угла.

Или так. Возьмите обыкновенную шестигранную гайку, положите ее плашмя на лист бумаги, и обведите контуры трех последовательных граней. У Вас получится три угла по 120 градусов и две параллельные прямые. Если их свободные концы чуть свести, чтобы они перестали быть параллельными, и продолжить до пересечения, то получим четырехугольник, один угол которого 120 градусов, еще два чуть меньше 120 градусов, и один очень острый, чуть больше 0.

Конечно можно начертить и множество промежуточных вариантов, необязательно симметричных. Просто приведенные примеры наиболее наглядны.

Из предложенного списка из 4-х фигур правильный ответ:треугольник.А прямоугольный треугольник-это уже частный случай.И так как теорема косинусов для произвольного треугольника :c^2=a^2+b^2-2b*a*cos 0 0

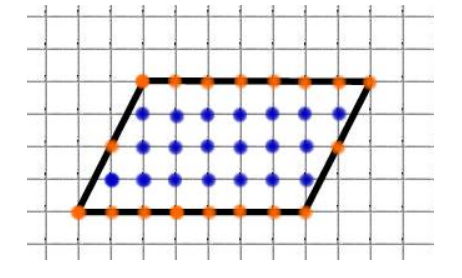
Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см).

Формула, о которой идет речь, называется формула Пика.

И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N — количество внутренних узлов.

Приведем пример, возьмем геометрическую фигуру параллелограмм:

Внутренние узлы — синие — N — их у нас 20.

Внешние узлы — красные — М — их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов.

Складываем 9 + 20 и вычитаем единицу: 20 + 9 — 1 = 28 см².

Источник