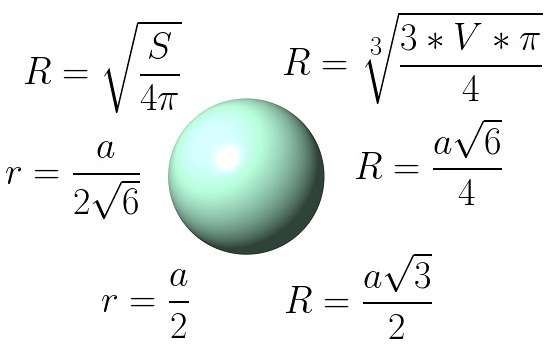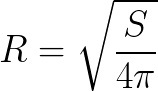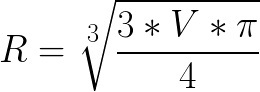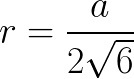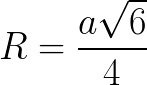Вычислить радиус сферы описанной вокруг куба с ребром длины a

Радиус вписанной сферы куба

Свойства

Радиус вписанной сферы куба представляет собой половину ребра куба, так как диаметр такой сферы точно совпадает с самим ребром. Поэтому чтобы найти ребро куба через радиус вписанной сферы, нужно умножить последний на два. (рис.2.2) a=2r

Найти площадь стороны куба можно как площадь квадрата, стороной которого является ребро куба. Тогда, вместо того чтобы возводить во вторую степень ребро, нужно возвести удвоенный радиус вписанной в куб сферы. Площадь боковой поверхности куба и площадь полной поверхности куба будут равны четырем и шести таким площадям соответственно, так как они представлены эти количеством граней куба. S=a^2=4r^2 S_(б.п.)=4S=16r^2 S_(п.п.)=6S=24r^2

Чтобы вычислить объем, необходимо возвести в куб ребро a или удвоенный радиус вписанной сферы. Таким образом, мы получим, что объем куба через радиус сферы, вписанной в него, равен кубу этого радиуса, умноженному на 8. V=a^3=8r^3

Периметр куба, как сумма длин всех ребер по одной стороне, равен произведению длины одного ребра и двенадцать. Периметр, выраженный через радиус вписанной окружности, равен 24 таким радиусам. P=12a=24r

Диагональ стороны куба, то есть диагональ квадрата, вычисляется как произведение ребра куба на корень из двух, в данном случае она будет выглядеть как произведение радиуса вписанной сферы на 2 корня из двух. d=a√2=2√2 r

Чтобы найти диагональ куба через радиус вписанной сферы, воспользуемся готовой формулой для диагонали куба через ребро и подставим вместо него удвоенный радиус. (рис.2.1.) D=a√3=2√3 r

Радиус окружности, описанной вокруг куба, равен половине диагонали, как видно из рисунка. Так как диагональ куба равна удвоенному произведению радиуса и корня из трех, то разделив это выражение на два, коэффициенты сократятся, и останется только радиус, умноженный на корень из трех. (рис.2.3.) R=D/2=(2√3 r)/2=√3 r

Источник

Радиус описанной сферы куба

Свойства

Если описать вокруг куба сферу, то ее диаметр будет соединять противоположные вершины куба, образуя диагональ куба. Таким образом, радиус описанной сферы куба равен половине диагонали, следовательно, сама диагональ куба равна удвоенному радиусу описанной сферы. (рис.2.3) D=2R

Так как эта же диагональ связывает теоремой Пифагора в прямоугольном треугольнике диагональ стороны куба и ребро куба, то становится возможным вычислить и их через радиус описанной сферы куба, используя формулы диагонали. D=a√3 a=D/√3=2R/√3 a^2+d^2=D^2 (2R/√3)^2+d^2=(2R)^2 d^2=(8R^2)/3 d=√(8/3) R

Чтобы вычислить площадь грани куба, нужно рассмотреть ее в плоскости. Стороной куба является квадрат, поэтому его площадь равна стороне квадрата, то есть ребру куба, во второй степени. Площадь боковой поверхности куба состоит из четырех боковых граней-квадратов, а площадь полной поверхности – из шести граней, поэтому для их вычисления нужно умножить площадь одной грани на их количество. Чтобы найти площади куба через радиус сферы, описанной вокруг него, нужно подставить вместо ребра куба удвоенный радиус, деленный на корень из трех. S=a^2=(2R/√3)^2=(4R^2)/3 S_(б.п.)=4S=(16R^2)/3 S_(п.п.)=6S=(24R^2)/3

Объем куба, зная радиус описанной вокруг него сферы, вычисляется возведением в третью степень выражения для ребра куба. V=a^3=(2R/√3)^3=(8R^3)/(3√3)

Периметр куба, как умноженное на 12 ребро куба, представлено через радиус описанной вокруг сферы окружности в виде отношения радиуса, умноженного на 24, к корню из трех. P=12a=24R/√3

Чтобы вычислить радиус сферы, вписанной в куб, через радиус сферы, описанной около него, нужно разделить ребро куба на два, то есть разделить радиус описанной сферы на корень из трех. r=a/2=2R/(2√3)=R/√3

Источник

Как найти радиус сферы

Перед тем, как смело броситься на амбразуру решения задачи по нахождению радиуса сферы, нужно узнать, что вообще такое сфера и шар. Стереометрия говорит нам, что сфера – это поверхность, состоящая из массы точек пространства, которые находятся на одном расстоянии от центра. Эта точка – центр сферы, а радиус сферы (R) – это расстояние, на которое каждая точка удалена от центра сферы. Шар – это тело, которое ограничено поверхностью сферы.

Безусловно, способ определения того самого радиуса сферы будет зависеть от данных, которые у нас есть.

Способ 1. Определение радиуса сферы при помощи площади ее поверхности

Допустим, нам дана сфера вместе с площадью её поверхности. В таком случае мы будем использовать формулу площади её поверхности для того, чтобы вычислить радиус.

где S – это площадь поверхности сферы, число Пи = 3,14.

Способ 2. Определение радиуса сферы при помощи объема шара

Если нам дан объём шара, ограниченного сферой, то радиус находится так:

где V — это объём шара, число Пи = 3,14.

Способ 3. Альтернативные формулы определения радиуса сферы

В случае, если наша сфера вписана в правильный многогранник или описана вокруг него, можно воспользоваться следующим рядом формул.

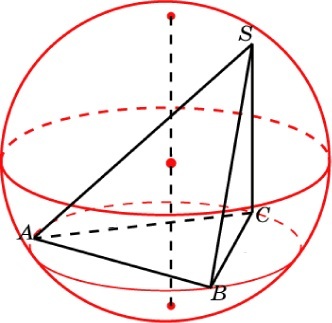
Формула 1. Сфера вписана в правильный тетраэдр

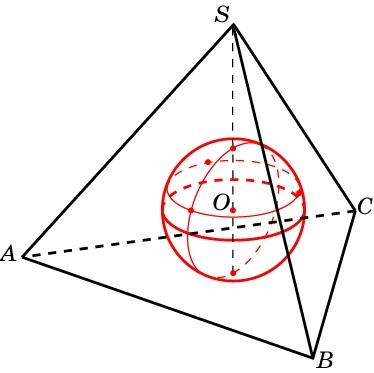
Для сферы, которая вписана в правильный тетраэдр:

где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).

Формула 2. Сфера описана около правильного тетраэдра

Для сферы, которая описана около правильного тетраэдра:

где a – длина ребра тетраэдра (AS = SB = AB = BC = SC = AC = a).

Источник

Нахождение радиуса описанной вокруг куба сферы (шара)

В данной публикации мы рассмотрим, чему равняется радиус сферы (шара), описанной около куба, а также как его можно вычислить, если известна длина ребра куба.

Примечание: Напомним, что вокруг любого куба можно описать шар.

Для начала начертим рисунок.

• все 8 вершин куба касаются шара – это их общие точки;
• центр шара – точка O, которая также является точкой пересечения диагоналей куба.

Радиус шара (R), описанного вокруг куба, равняется половине его диагонали, т.е.:

Примечание: все диагонали куба равны.

Чтобы было понятнее, выполним диагональное сечение, т.е. отсечем часть шара вместе со вписанным в него кубом по диагонали куба (линия отреза проходит через точку O).

Таким образом, мы получим прямоугольник с описанной вокруг окружностью, радиус которой равняется половине диагонали прямоугольника.

Примечание: Диагонали прямоугольника равны между собой и одновременно являются диагоналями куба.

Формула расчета радиуса описанного шара через ребро куба

Если известна длина ребра куба (примем ее за “a”), радиус описанного вокруг него шара (R) вычисляется следующим образом:

Источник

Нахождение радиуса вписанного в куб шара

В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.

Примечание: Напомним, что в любой куб можно вписать шар.

Для начала выполним чертеж.

• шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
• центр шара – точка O, которая также является центром куба.

Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:

R = a/2, где “a” – ребро куба (является стороной его грани).

Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.

Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.

Радиус вписанного шара через диагональ куба

Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:

Источник

Радиус вписанной сферы куба

Свойства

Радиус вписанной сферы куба представляет собой половину ребра куба, так как диаметр такой сферы точно совпадает с самим ребром. Поэтому чтобы найти ребро куба через радиус вписанной сферы, нужно умножить последний на два. (рис.2.2) a=2r

Найти площадь стороны куба можно как площадь квадрата, стороной которого является ребро куба. Тогда, вместо того чтобы возводить во вторую степень ребро, нужно возвести удвоенный радиус вписанной в куб сферы. Площадь боковой поверхности куба и площадь полной поверхности куба будут равны четырем и шести таким площадям соответственно, так как они представлены эти количеством граней куба. S=a^2=4r^2 S_(б.п.)=4S=16r^2 S_(п.п.)=6S=24r^2

Чтобы вычислить объем, необходимо возвести в куб ребро a или удвоенный радиус вписанной сферы. Таким образом, мы получим, что объем куба через радиус сферы, вписанной в него, равен кубу этого радиуса, умноженному на 8. V=a^3=8r^3

Периметр куба, как сумма длин всех ребер по одной стороне, равен произведению длины одного ребра и двенадцать. Периметр, выраженный через радиус вписанной окружности, равен 24 таким радиусам. P=12a=24r

Диагональ стороны куба, то есть диагональ квадрата, вычисляется как произведение ребра куба на корень из двух, в данном случае она будет выглядеть как произведение радиуса вписанной сферы на 2 корня из двух. d=a√2=2√2 r

Чтобы найти диагональ куба через радиус вписанной сферы, воспользуемся готовой формулой для диагонали куба через ребро и подставим вместо него удвоенный радиус. (рис.2.1.) D=a√3=2√3 r

Радиус окружности, описанной вокруг куба, равен половине диагонали, как видно из рисунка. Так как диагональ куба равна удвоенному произведению радиуса и корня из трех, то разделив это выражение на два, коэффициенты сократятся, и останется только радиус, умноженный на корень из трех. (рис.2.3.) R=D/2=(2√3 r)/2=√3 r

Источник

Вычислить радиус сферы описанной вокруг куба с ребром длины a

Объём куба, описанного около сферы, равен 1331. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 1000. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 1728. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Площадь поверхности куба, описанного около сферы, равна 96. Найдите радиус сферы.

Площадь поверхности куба равна суммарной площади площади шести квадратов, составляющих его грани. Следовательно, длина ребра куба равна

Радиус сферы равен половине длины ребра куба.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 343. Найдите радиус сферы.

Это задание ещё не решено, приводим решение прототипа.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 15625. Найдите радиус сферы.

Это задание ещё не решено, приводим решение прототипа.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 4096. Найдите радиус сферы.

Это задание ещё не решено, приводим решение прототипа.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 2197. Найдите радиус сферы.

Это задание ещё не решено, приводим решение прототипа.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 9261. Найдите радиус сферы.

Это задание ещё не решено, приводим решение прототипа.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 8. Найдите радиус сферы.

Это задание ещё не решено, приводим решение прототипа.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 125. Найдите радиус сферы.

Это задание ещё не решено, приводим решение прототипа.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 1. Найдите радиус сферы.

Это задание ещё не решено, приводим решение прототипа.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Объём куба, описанного около сферы, равен 13824. Найдите радиус сферы.

Это задание ещё не решено, приводим решение прототипа.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра

Радиус сферы равен половине длины ребра

Источник