В кубе ad1 найти угол между плоскостями

Задача 34765 7. В кубе А. D1, найдите угол между.

Условие

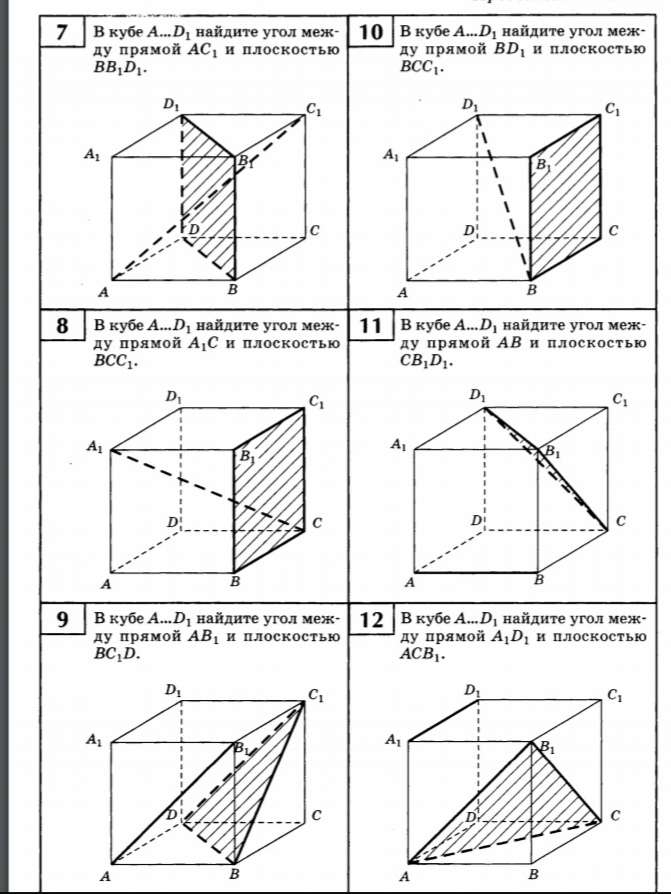
7. В кубе А. D1, найдите угол между прямой АС1, и плоскостью BB1D1

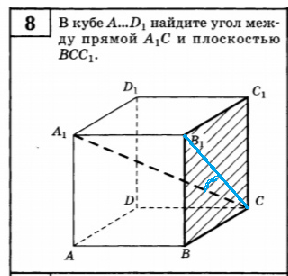
8. В кубе A. D1, найдите угол между прямой А1С и плоскостью BCC1.

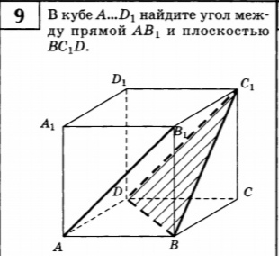
9. В кубе А. D1, найдите угол между прямой АВ1, и плоскостью BC1D

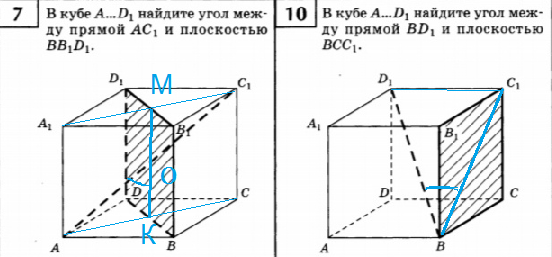
10. В кубе А. D1, найдите угол между прямой BD1 и плоскостью ВСС1.

11. В кубе А. D1, найдите угол между прямой АВ и плоскостью СВ1D1.

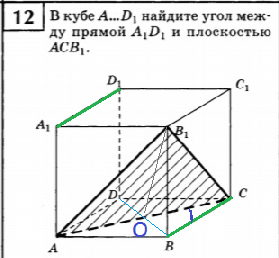
12. В кубе А. D1, найдите угол между прямой А1D1 и плоскостью АСВ1.

Решение

7.
Угол между прямой и плоскостью — угол между прямой и ее проекцией на плоскость.
Проводим A_(1)C_(1) ⊥ B_(1)D_(1)
и АС ⊥ BD

Проекцией АС_(1) является MK
Угол АОК — искомый, находим из треугольника AOK
[b]tg ∠ AOK[/b]=AK/OK=sqrt(2)/2/1/2= [b]sqrt(2)[/b]

О т в е т. ∠ AOK= arctg(sqrt(2))

10.
Угол между прямой и плоскостью — угол между прямой и ее проекцией на плоскость.
Проекцией BD_(1) является BС_(1).

Угол C_(1)BD_(1) — искомый, находим из треугольника C_(1)BD_(1)

tg ∠ C_(1)BD_(1)=C_(1)D_(1)/BC_(1)=1/sqrt(2)=sqrt(2)/2
∠ C_(1)BD_(1)=arctg (sqrt(2)/2)

О т в е т. ∠ C_(1)BD_(1)=arctg (sqrt(2)/2)

8.
Угол между прямой и плоскостью — угол между прямой и ее проекцией на плоскость.
Проекцией A_(1)C является B_(1)C.

Угол A_(1)BC_(1) — искомый, находим из треугольника A_(1)BC_(1)

tg ∠ A_(1)BC_(1)=A_(1)B_(1)/B_(1)C=1/sqrt(2)=sqrt(2)/2
∠∠ A_(1)BC_(1)=arctg (sqrt(2)/2)

О т в е т. ∠ A_(1)BC_(1)=arctg (sqrt(2)/2)

AC⊥ BO
B_(1)O — медиана равнобедренного треугольника АВ_(1)С
Значит, B_(1)O⊥ AC

АС ⊥ пл. В_(1)ОВ, так как перпендикулярна двум пересекающимся прямым этой плоскости BO и B_(1)O.

⇒ ОС- проекция ВС,
угол между ОС и ВС — это угол АСВ он равен 45 градусов

Значит угол между A_(1)D_(1) и пл. АВ_(1)С равен 45 градусов

11.
Как в 12.
∠ А_(1)В_(1)О= 45 градусов.

AB_(1) || пл. DС_(1)B
Значит угол между ними 0 градусов.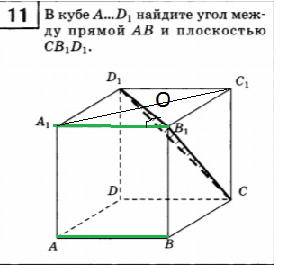

Источник

В кубе A…D1 найдите угол между плоскостями ABC и CDD1

В кубе A…D1 найдите угол между плоскостями ABC и CDD1. Задача 1: Ответ: 90o.

Слайд 8 из презентации «Двугранный угол»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Двугранный угол.pptx» можно в zip-архиве размером 306 КБ.

Углы в пространстве

«Величина двугранного угла» — Найти величину двугранного угла. Линейный угол РDСВ. Что называется углом на плоскости. Задачи на построение линейного угла. Дан ромб АВСD. Угол между плоскостями АСН и СНD – это двугранный угол АСНD. Расстояние от точки до плоскости. Алгоритм построения линейного угла. Фигура, образованная двумя полуплоскостями.

«Угол между прямыми в пространстве» — В кубе A…D1 найдите угол между прямыми: AB1 и BD1. Угол между прямыми в пространстве. В кубе A…D1 найдите угол между прямыми: AA1 и BC1. В кубе A…D1 найдите угол между прямыми: A1C1 и B1D1. В кубе A…D1 найдите угол между прямыми: AB1 и BC1. В кубе A…D1 найдите угол между прямыми: AA1 и BC. В кубе A…D1 найдите угол между прямыми: AA1 и BD1.

«Трёхгранный угол» — Следствие. Формула трех косинусов. Урок 6. В правильной треугольной пирамиде плоский угол при вершине меньше 120?. . Дан трехгранный угол Оabc. Признаки равенства трехгранных углов. Определение. Заменим: Следствия. 1) Для вычисления угла между прямой и плоскостью применима формула: Трехгранный угол.

Источник

Презентация по математике «Угол между плоскостями»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

ДВУГРАННЫЙ УГОЛ. УГОЛ МЕЖДУ ПЛОСКОСТЯМИ Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой. Линейным углом двугранного угла называется угол, образованный лучами с вершиной на граничной прямой, стороны которого лежат на гранях двугранного угла и перпендикулярны граничной прямой. Величиной двугранного угла называется величина его линейного угла. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.

В кубе A…D1 найдите угол между плоскостями ABC и CDD1. Ответ: 90o.

В кубе A…D1 найдите угол между плоскостями ABC и CDA1. Ответ: 45o.

В кубе A…D1 найдите угол между плоскостями ABC и BDD1. Ответ: 90o.

В кубе A…D1 найдите угол между плоскостями ABC и BC1D.

В кубе A…D1 найдите угол между плоскостями ABC и BC1D. Решение: Обозначим O середину BD. Искомым линейным углом будет угол COC1. В прямоугольном треугольнике COC1 имеем CC1 = 1; CO = Следовательно,

В кубе A…D1 найдите угол между плоскостями ABC и AB1D1.

В кубе A…D1 найдите угол между плоскостями ACC1 и BDD1. Ответ: 90o.

В кубе A…D1 найдите угол между плоскостями ABC1 и BB1D1.

В кубе A…D1 найдите угол между плоскостями ABC1 и BB1D1. Решение: Заметим, что плоскость равностороннего треугольника ACB1 перпендикулярна диагонали BD1, которая проходит через центр O этого треугольника. Искомым линейным углом будет угол B1OE, который равен 60o. Ответ: 60o.

В кубе A…D1 найдите угол между плоскостями BC1D1 и BA1D. Ответ: 90o. Решение: Заметим, что плоскость равностороннего треугольника BDA1 перпендикулярна диагонали AC1, которая проходит через центр этого треугольника. Следовательно, данные плоскости перпендикулярны. Искомый угол равен 90o.

В кубе A…D1 найдите угол между плоскостями BC1D и BA1D.

В кубе A…D1 найдите угол между плоскостями BC1D и BA1D. Решение: Пусть O – середина BD. Искомый угол равен углу A1OC1. Имеем Используя теорему косинусов, получим Ответ:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 595 788 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Добавить в избранное

• 28.09.2016 16056
• PPTX 247 кбайт
• 79 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Покотилова Александра Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

РДШ организовало сбор гуманитарной помощи для детей из ДНР

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Нахождение угла между плоскостями (двугранный угол)

\(\blacktriangleright\) Двугранный угол – угол, образованный двумя полуплоскостями и прямой \(a\) , которая является их общей границей.

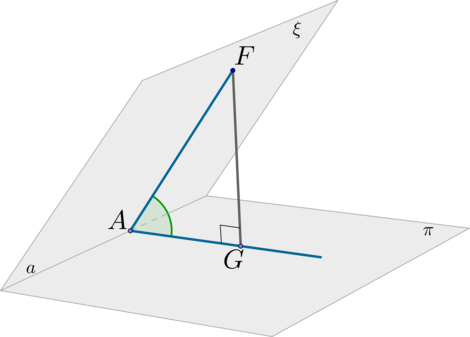
\(\blacktriangleright\) Чтобы найти угол между плоскостями \(\xi\) и \(\pi\) , нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями \(\xi\) и \(\pi\) :

Шаг 1: пусть \(\xi\cap\pi=a\) (линия пересечения плоскостей). В плоскости \(\xi\) отметим произвольную точку \(F\) и проведем \(FA\perp a\) ;

Шаг 3: по ТТП ( \(FG\) – перпендикуляр, \(FA\) –наклонная, \(AG\) – проекция) имеем: \(AG\perp a\) ;

Шаг 4: угол \(\angle FAG\) называется линейным углом двугранного угла, образованного плоскостями \(\xi\) и \(\pi\) .

Заметим, что треугольник \(AG\) – прямоугольный.
Заметим также, что плоскость \(AFG\) , построенная таким образом, перпендикулярна обеим плоскостям \(\xi\) и \(\pi\) . Следовательно, можно сказать по-другому: угол между плоскостями \(\xi\) и \(\pi\) — это угол между двумя пересекающимися прямыми \(c\in \xi\) и \(b\in\pi\) , образующими плоскость, перпендикулярную и \(\xi\) , и \(\pi\) .

Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите \(6\cos \alpha\) , где \(\alpha\) – угол между ее смежными боковыми гранями.

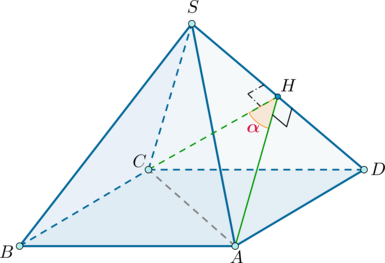
Пусть \(SABCD\) – данная пирамида ( \(S\) – вершина), ребра которой равны \(a\) . Следовательно, все боковые грани представляют собой равные равносторонние треугольники. Найдем угол между гранями \(SAD\) и \(SCD\) .

Проведем \(CH\perp SD\) . Так как \(\triangle SAD=\triangle SCD\) , то \(AH\) также будет высотой в \(\triangle SAD\) . Следовательно, по определению \(\angle AHC=\alpha\) – линейный угол двугранного угла между гранями \(SAD\) и \(SCD\) .
Так как в основании лежит квадрат, то \(AC=a\sqrt2\) . Заметим также, что \(CH=AH\) – высота равностороннего треугольника со стороной \(a\) , следовательно, \(CH=AH=\frac<\sqrt3>2a\) .
Тогда по теореме косинусов из \(\triangle AHC\) : \[\cos \alpha=\dfrac<2CH\cdot AH>=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

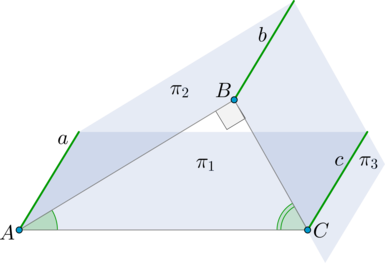
Плоскости \(\pi_1\) и \(\pi_2\) пересекаются под углом, косинус которого равен \(0,2\) . Плоскости \(\pi_2\) и \(\pi_3\) пересекаются под прямым углом, причем линия пересечения плоскостей \(\pi_1\) и \(\pi_2\) параллельна линии пересечения плоскостей \(\pi_2\) и \(\pi_3\) . Найдите синус угла между плоскостями \(\pi_1\) и \(\pi_3\) .

Пусть линия пересечения \(\pi_1\) и \(\pi_2\) – прямая \(a\) , линия пересечения \(\pi_2\) и \(\pi_3\) – прямая \(b\) , а линия пересечения \(\pi_3\) и \(\pi_1\) – прямая \(c\) . Так как \(a\parallel b\) , то \(c\parallel a\parallel b\) (по теореме из раздела теоретической справки “Геометрия в пространстве” \(\rightarrow\) “Введение в стереометрию, параллельность”).

Отметим точки \(A\in a, B\in b\) так, чтобы \(AB\perp a, AB\perp b\) (это возможно, так как \(a\parallel b\) ). Отметим \(C\in c\) так, чтобы \(BC\perp c\) , следовательно, \(BC\perp b\) . Тогда \(AC\perp c\) и \(AC\perp a\) .
Действительно, так как \(AB\perp b, BC\perp b\) , то \(b\) перпендикулярна плоскости \(ABC\) . Так как \(c\parallel a\parallel b\) , то прямые \(a\) и \(c\) тоже перпендикулярны плоскости \(ABC\) , а значит и любой прямой из этой плоскости, в частности, прямой \(AC\) .

Отсюда следует, что \(\angle BAC=\angle (\pi_1, \pi_2)\) , \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\) , \(\angle BCA=\angle (\pi_3, \pi_1)\) . Получается, что \(\triangle ABC\) прямоугольный, а значит \[\sin \angle BCA=\cos \angle BAC=0,2.\]

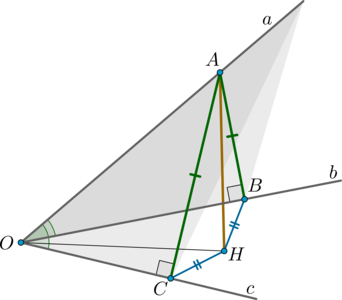
Даны прямые \(a, b, c\) , пересекающиеся в одной точке, причем угол между любыми двумя из них равен \(60^\circ\) . Найдите \(\cos^<-1>\alpha\) , где \(\alpha\) – угол между плоскостью, образованной прямыми \(a\) и \(c\) , и плоскостью, образованной прямыми \(b\) и \(c\) . Ответ дайте в градусах.

Пусть прямые пересекаются в точке \(O\) . Так как угол между любыми двумя их них равен \(60^\circ\) , то все три прямые не могут лежать в одной плоскости. Отметим на прямой \(a\) точку \(A\) и проведем \(AB\perp b\) и \(AC\perp c\) . Тогда \(\triangle AOB=\triangle AOC\) как прямоугольные по гипотенузе и острому углу. Следовательно, \(OB=OC\) и \(AB=AC\) .
Проведем \(AH\perp (BOC)\) . Тогда по теореме о трех перпендикулярах \(HC\perp c\) , \(HB\perp b\) . Так как \(AB=AC\) , то \(\triangle AHB=\triangle AHC\) как прямоугольные по гипотенузе и катету. Следовательно, \(HB=HC\) . Значит, \(OH\) – биссектриса угла \(BOC\) (так как точка \(H\) равноудалена от сторон угла).

Заметим, что таким образом мы к тому же построили линейный угол двугранного угла, образованного плоскостью, образованной прямыми \(a\) и \(c\) , и плоскостью, образованной прямыми \(b\) и \(c\) . Это угол \(ACH\) .

Найдем этот угол. Так как точку \(A\) мы выбирали произвольно, то пусть мы выбрали ее так, что \(OA=2\) . Тогда в прямоугольном \(\triangle AOC\) : \[\sin 60^\circ=\dfrac \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt=1.\] Так как \(OH\) – биссектриса, то \(\angle HOC=30^\circ\) , следовательно, в прямоугольном \(\triangle HOC\) : \[\mathrm\,30^\circ=\dfrac\quad\Rightarrow\quad HC=\dfrac1<\sqrt3>.\] Тогда из прямоугольного \(\triangle ACH\) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac=\dfrac13 \quad\Rightarrow\quad \cos^<-1>\alpha=3.\]

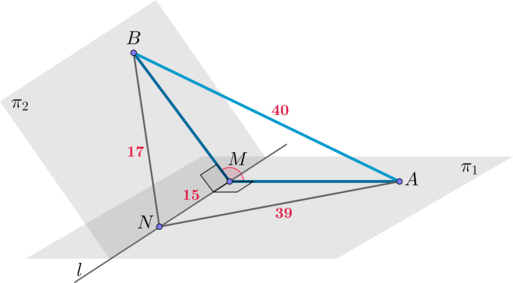
Плоскости \(\pi_1\) и \(\pi_2\) пересекаются по прямой \(l\) , на которой лежат точки \(M\) и \(N\) . Отрезки \(MA\) и \(MB\) перпендикулярны прямой \(l\) и лежат в плоскостях \(\pi_1\) и \(\pi_2\) соответственно, причем \(MN = 15\) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Найдите \(3\cos\alpha\) , где \(\alpha\) – угол между плоскостями \(\pi_1\) и \(\pi_2\) .

Треугольник \(AMN\) прямоугольный, \(AN^2 = AM^2 + MN^2\) , откуда \[AM^2 = 39^2 — 15^2 = 36^2.\] Треугольник \(BMN\) прямоугольный, \(BN^2 = BM^2 + MN^2\) , откуда \[BM^2 = 17^2 — 15^2 = 8^2.\] Запишем для треугольника \(AMB\) теорему косинусов: \[AB^2 = AM^2 + MB^2 — 2\cdot AM\cdot MB\cdot\cos\angle AMB.\] Тогда \[40^2 = 36^2 + 8^2 — 2\cdot 36\cdot 8\cdot\cos\angle AMB\qquad\Leftrightarrow\qquad \cos\angle AMB = -\dfrac<5><12>\] Так как угол \(\alpha\) между плоскостями – это острый угол, а \(\angle AMB\) получился тупым, то \(\cos\alpha=\dfrac5<12>\) . Тогда \[3\cos\alpha = \dfrac54=1,25.\]

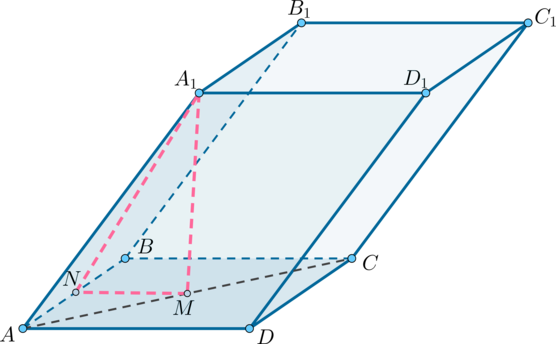
\(ABCDA_1B_1C_1D_1\) – параллелепипед, \(ABCD\) – квадрат со стороной \(a\) , точка \(M\) – основание перпендикуляра, опущенного из точки \(A_1\) на плоскость \((ABCD)\) , кроме того \(M\) – точка пересечения диагоналей квадрата \(ABCD\) . Известно, что \(A_1M = \dfrac<\sqrt<3>><2>a\) . Найдите угол между плоскостями \((ABCD)\) и \((AA_1B_1B)\) . Ответ дайте в градусах.

Построим \(MN\) перпендикулярно \(AB\) как показано на рисунке.

Так как \(ABCD\) – квадрат со стороной \(a\) и \(MN\perp AB\) и \(BC\perp AB\) , то \(MN\parallel BC\) . Так как \(M\) – точка пересечения диагоналей квадрата, то \(M\) – середина \(AC\) , следовательно, \(MN\) – средняя линия и \(MN =\frac12BC= \frac<1><2>a\) .
\(MN\) – проекция \(A_1N\) на плоскость \((ABCD)\) , причем \(MN\) перпендикулярен \(AB\) , тогда по теореме о трех перпендикулярах \(A_1N\) перпендикулярен \(AB\) и угол между плоскостями \((ABCD)\) и \((AA_1B_1B)\) есть \(\angle A_1NM\) .
\[\mathrm\, \angle A_1NM = \dfrac = \dfrac<\frac<\sqrt<3>><2>a><\frac<1><2>a> = \sqrt<3>\qquad\Rightarrow\qquad\angle A_1NM = 60^<\circ>\]

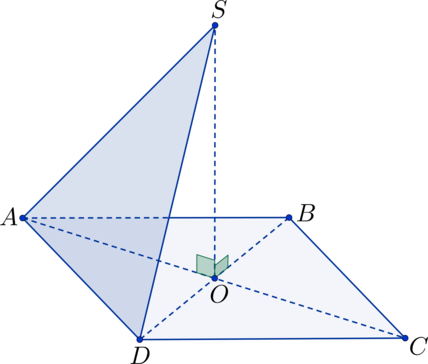
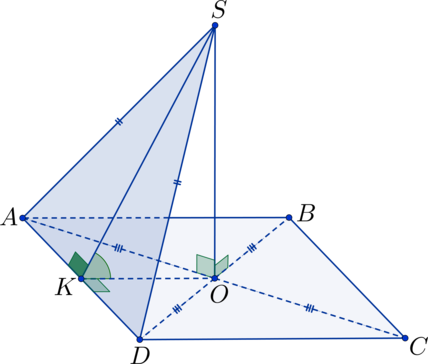
В квадрате \(ABCD\) : \(O\) – точка пересечения диагоналей; \(S\) – не лежит в плоскости квадрата, \(SO \perp ABC\) . Найдите угол между плоскостями \(ASD\) и \(ABC\) , если \(SO = 5\) , а \(AB = 10\) .

Прямоугольные треугольники \(\triangle SAO\) и \(\triangle SDO\) равны по двум сторонам и углу между ними ( \(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\) ; \(AO = DO\) , т.к. \(O\) – точка пересечения диагоналей квадрата, \(SO\) – общая сторона) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\triangle ASD\) – равнобедренный. Точка \(K\) – середина \(AD\) , тогда \(SK\) – высота в треугольнике \(\triangle ASD\) , а \(OK\) – высота в треугольнике \(AOD\) \(\Rightarrow\) плоскость \(SOK\) перпендикулярна плоскостям \(ASD\) и \(ABC\) \(\Rightarrow\) \(\angle SKO\) – линейный угол, равный искомому двугранному углу.

В \(\triangle SKO\) : \(OK = \frac<1><2>\cdot AB = \frac<1><2>\cdot 10 = 5 = SO\) \(\Rightarrow\) \(\triangle SOK\) – равнобедренный прямоугольный треугольник \(\Rightarrow\) \(\angle SKO = 45^\circ\) .

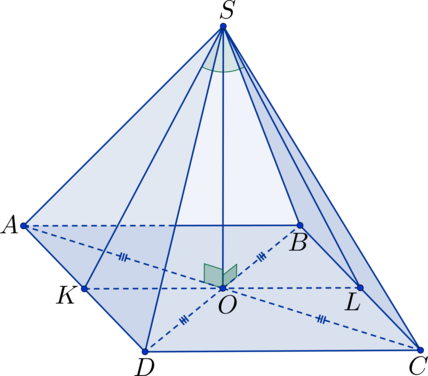
В квадрате \(ABCD\) : \(O\) – точка пересечения диагоналей; \(S\) – не лежит в плоскости квадрата, \(SO \perp ABC\) . Найдите угол между плоскостями \(ASD\) и \(BSC\) , если \(SO = 5\) , а \(AB = 10\) .

Прямоугольные треугольники \(\triangle SAO\) , \(\triangle SDO\) , \(\triangle SOB\) и \(\triangle SOC\) равны по двум сторонам и углу между ними ( \(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\) ; \(AO = OD = OB = OC\) , т.к. \(O\) – точка пересечения диагоналей квадрата, \(SO\) – общая сторона) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \(\triangle ASD\) и \(\triangle BSC\) – равнобедренные. Точка \(K\) – середина \(AD\) , тогда \(SK\) – высота в треугольнике \(\triangle ASD\) , а \(OK\) – высота в треугольнике \(AOD\) \(\Rightarrow\) плоскость \(SOK\) перпендикулярна плоскости \(ASD\) . Точка \(L\) – середина \(BC\) , тогда \(SL\) – высота в треугольнике \(\triangle BSC\) , а \(OL\) – высота в треугольнике \(BOC\) \(\Rightarrow\) плоскость \(SOL\) (она же плоскость \(SOK\) ) перпендикулярна плоскости \(BSC\) . Таким образом получаем, что \(\angle KSL\) – линейный угол, равный искомому двугранному углу.

\(KL = KO + OL = 2\cdot OL = AB = 10\) \(\Rightarrow\) \(OL = 5\) ; \(SK = SL\) – высоты в равных равнобедренных треугольниках, которые можно найти по теореме Пифагора: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\) . Можно заметить, что \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\) \(\Rightarrow\) для треугольника \(\triangle KSL\) выполняется обратная теорема Пифагора \(\Rightarrow\) \(\triangle KSL\) – прямоугольный треугольник \(\Rightarrow\) \(\angle KSL = 90^\circ\) .

Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями. Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала. Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.

Основные нюансы

Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ.

Вначале необходимо определить прямую, по которой пересекаются плоскости.

Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра.

Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол.

Ответом будет значение угла или его тригонометрической функции.

Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха

В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями. Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо. А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.

Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.

Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».

Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на нахождение угла между прямой и плоскостью, представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.

Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.

Источник