В кубе abcda1b1c1d1 сторона основания равна 5 постройте линейный

Презентация «Решение заданий ЕГЭ профильного уровня по стереометрии». Часть 3.

Часть 3. Решение заданий ЕГЭ по стереометрии профильного уровня

Решение заданий ЕГЭ по стереометрии профильного уровня.

В правильной треугольной призме

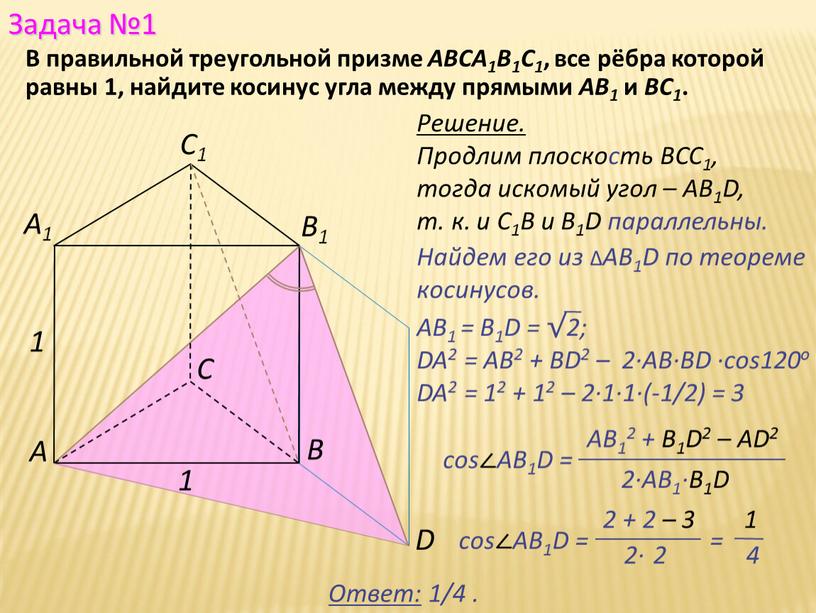
В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 1, найдите косинус угла между прямыми АВ1 и ВС1.

Решение.
Продлим плоскость ВСС1, тогда искомый угол – AВ1D, т. к. и C1В и B1D параллельны.

Найдем его из ∆AB1D по теореме косинусов.

В правильной шестиугольной призме

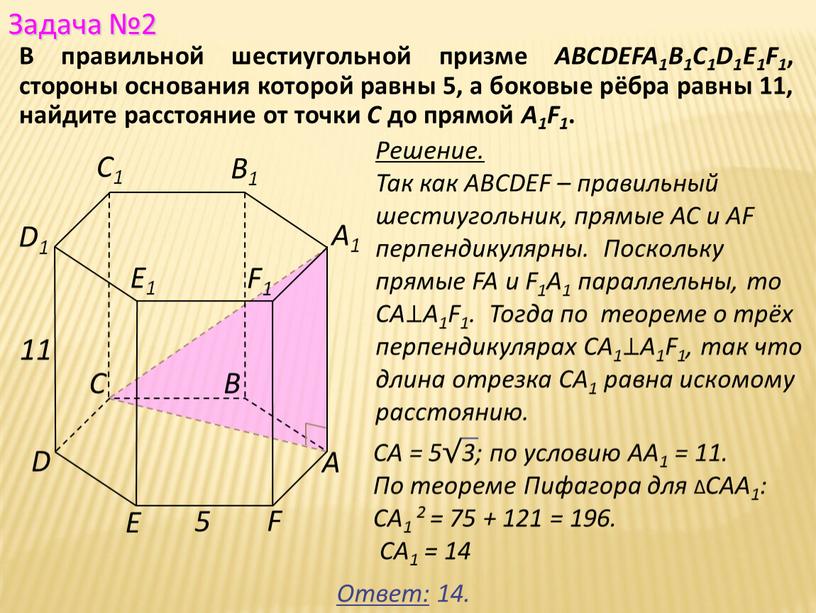
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки С до прямой A1F1.

Решение.
Так как ABCDEF – правильный шестиугольник, прямые AC и AF перпендикулярны. Поскольку прямые FA и F1A1 параллельны, то
CA⊥A1F1. Тогда по теореме о трёх перпендикулярах CA1⊥A1F1, так что длина отрезка CA1 равна искомому расстоянию.

Решение. Так как ABCD – квадрат, то прямые

Решение.
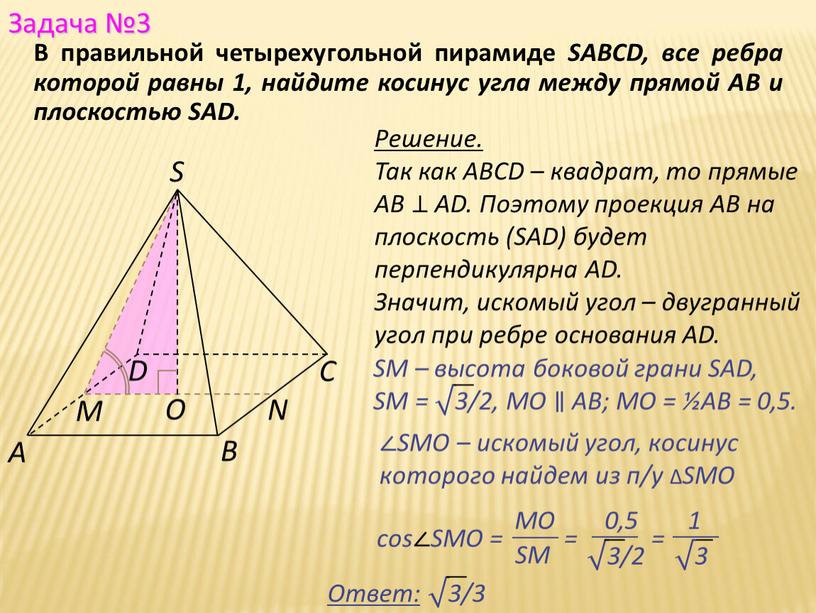
Так как ABCD – квадрат, то прямые АВ ⊥ AD. Поэтому проекция AB на плоскость (SAD) будет перпендикулярна AD.
Значит, искомый угол – двугранный угол при ребре основания AD.

В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите косинус угла между прямой AB и плоскостью SAD.

∠SMO – искомый угол, косинус которого найдем из п/у ∆SMO

В кубе ABCDA1B1C1D1 найдите угол между прямой

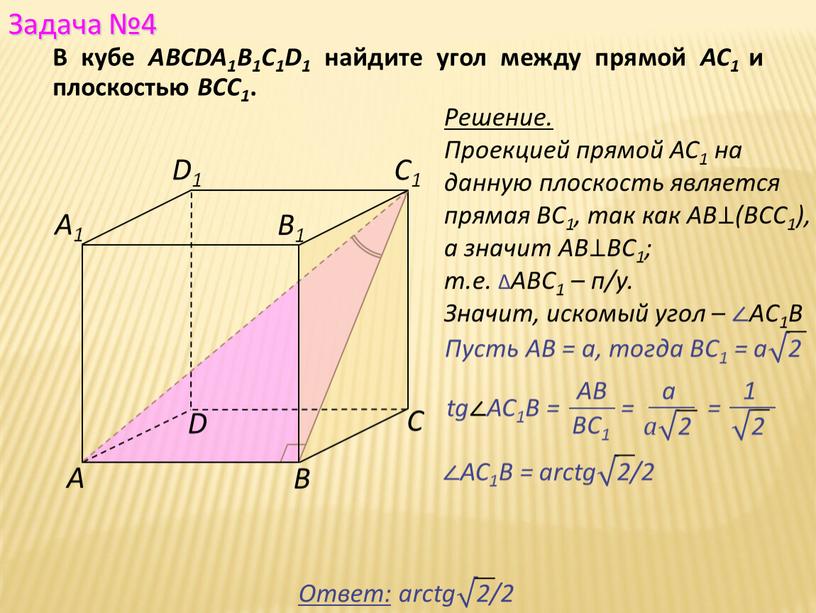
В кубе ABCDA1B1C1D1 найдите угол между прямой AC1 и плоскостью ВСC1.

Решение.
Проекцией прямой АС1 на данную плоскость является прямая ВС1, так как AB⊥(ВCС1), а значит AB⊥ВС1;
т.е. ∆АВC1 – п/у.
Значит, искомый угол – ∠AС1В

В правильной четырехугольной призме

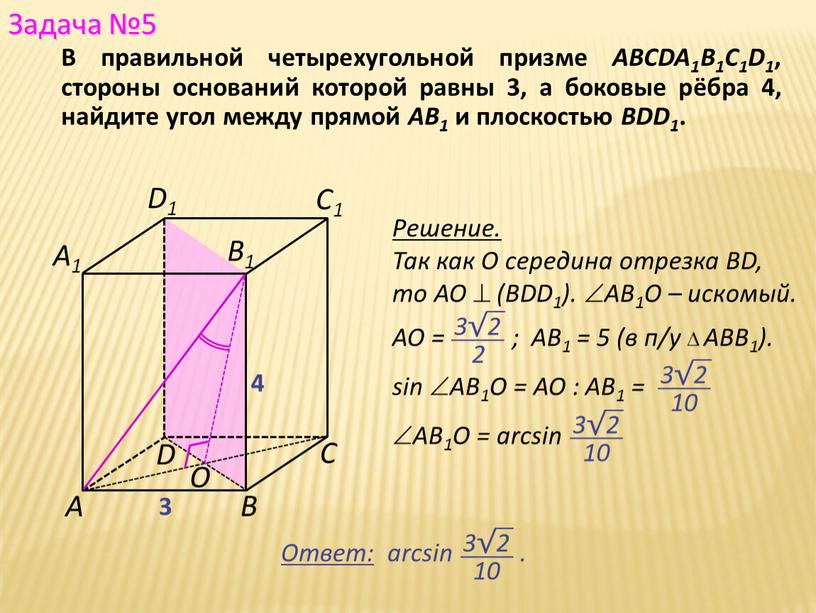
В правильной четырехугольной призме ABCDA1B1C1D1, стороны оснований которой равны 3, а боковые рёбра 4, найдите угол между прямой АВ1 и плоскостью BDD1.

Решение. Прямая AN является проекцией прямой

Решение.
Прямая AN является проекцией прямой AS на плоскость основания.
Поэтому проекция точки М – точка Н лежит на отрезке AN. Значит угол MNH – искомый.
МН – средняя линия SAO,
тогда NH = АО = R = = = 24.

В правильной четырехугольной призме

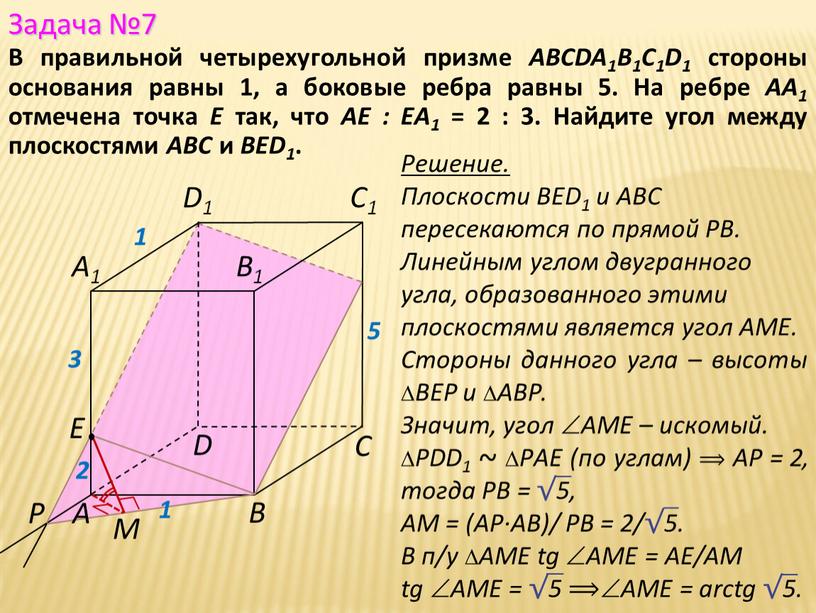
В правильной четырехугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые ребра равны 5. На ребре АА1 отмечена точка Е так, что АЕ : ЕА1 = 2 : 3. Найдите угол между плоскостями АВС и BED1.

Решение.
Плоскости BED1 и АВС пересекаются по прямой PB.
Линейным углом двугранного угла, образованного этими плоскостями является угол АМЕ.
Стороны данного угла – высоты ВЕР и AВР.
Значит, угол АMЕ – искомый.
РDD1

Дан куб ABCDA1B1C1D1 . Найдите угол между плоскостями

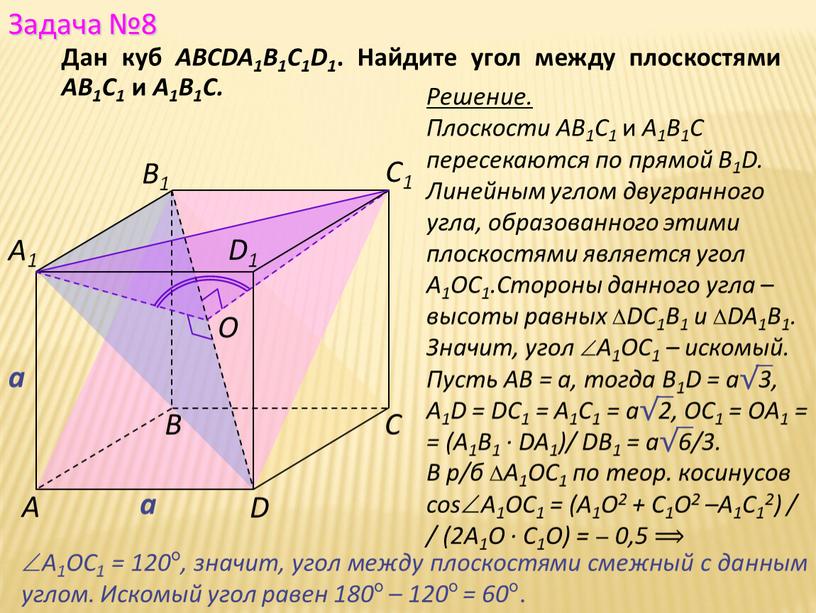
Дан куб ABCDA1B1C1D1. Найдите угол между плоскостями АВ1С1 и А1В1С.

Решение.
Плоскости АВ1С1 и А1В1С пересекаются по прямой B1D.
Линейным углом двугранного угла, образованного этими плоскостями является угол А1ОС1.Стороны данного угла – высоты равных DС1B1 и DA1В1.
Значит, угол A1OС1 – искомый.
Пусть АВ = а, тогда B1D = a√3,
А1D = DC1 = A1C1 = a√2, OC1 = OA1 =
= (А1B1 · DA1)/ DВ1 = a√6/3.
В р/б A1OC1 по теор. косинусов
cosA1OC1 = (A1О2 + C1О2 –А1C12) /
/ (2А1О · C1О) = − 0,5 ⟹

A1OC1 = 120º, значит, угол между плоскостями смежный с данным углом. Искомый угол равен 180º – 120º = 60º.

Основанием прямой треугольной призмы

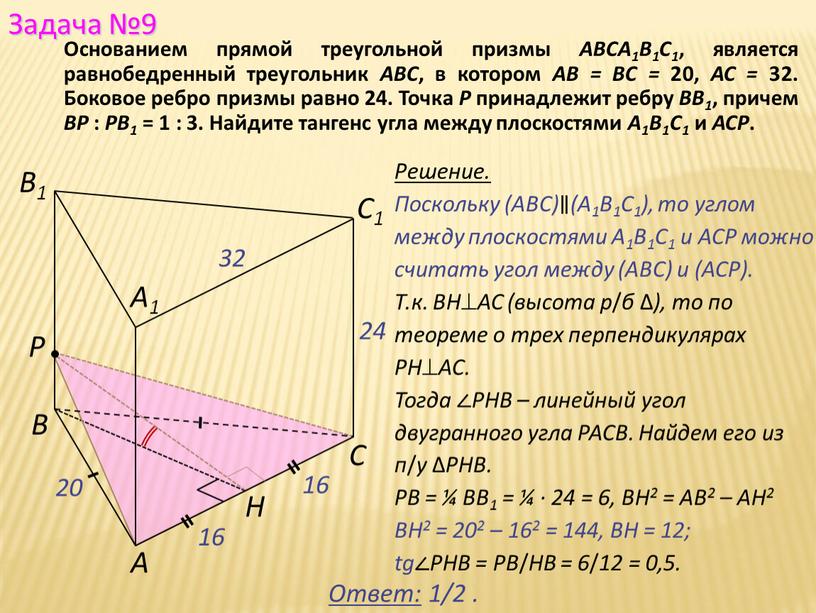
Основанием прямой треугольной призмы ABCA1B1C1, является равнобедренный треугольник АВС, в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка Р принадлежит ребру ВВ1, причем ВР : РВ1 = 1 : 3. Найдите тангенс угла между плоскостями А1В1С1 и АСР.

Решение.
Поскольку (АВС)∥(А1В1С1), то углом между плоскостями А1В1С1 и АСР можно считать угол между (АВС) и (АСР).
Т.к. ВНАС (высота р/б ∆), то по теореме о трех перпендикулярах РНАС.
Тогда ∠РНВ – линейный угол двугранного угла РАСВ. Найдем его из п/у ∆РНВ.
РВ = ¼ ВВ1 = ¼ · 24 = 6, ВН2 = АВ2 – АН2
ВН2 = 202 – 162 = 144, ВН = 12;
tg∠РНВ = PB/HB = 6/12 = 0,5.

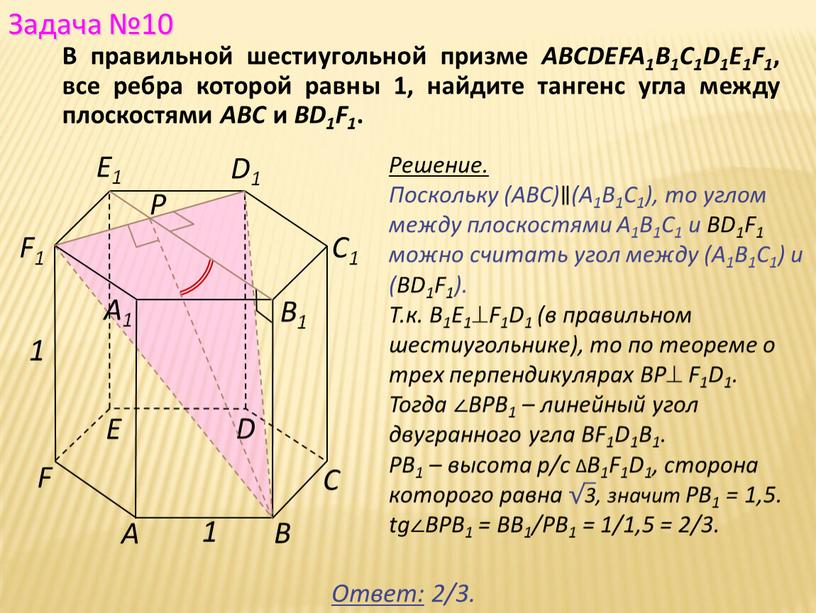
Решение. Поскольку (АВС) ∥ (А1В1С1), то углом между плоскостями

Решение.
Поскольку (АВС)∥(А1В1С1), то углом между плоскостями А1В1С1 и BD1F1 можно считать угол между (А1В1С1) и (BD1F1).
Т.к. В1E1F1D1 (в правильном шестиугольнике), то по теореме о трех перпендикулярах ВР F1D1.
Тогда ∠BРВ1 – линейный угол двугранного угла BF1D1В1.
PB1 – высота р/с ∆В1F1D1, сторона которого равна √3, значит PB1 = 1,5.
tg∠BРВ1 = BB1/PB1 = 1/1,5 = 2/3.

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите тангенс угла между плоскостями АВС и BD1F1.

Решение. (1 способ) Искомое расстояние равно высоте

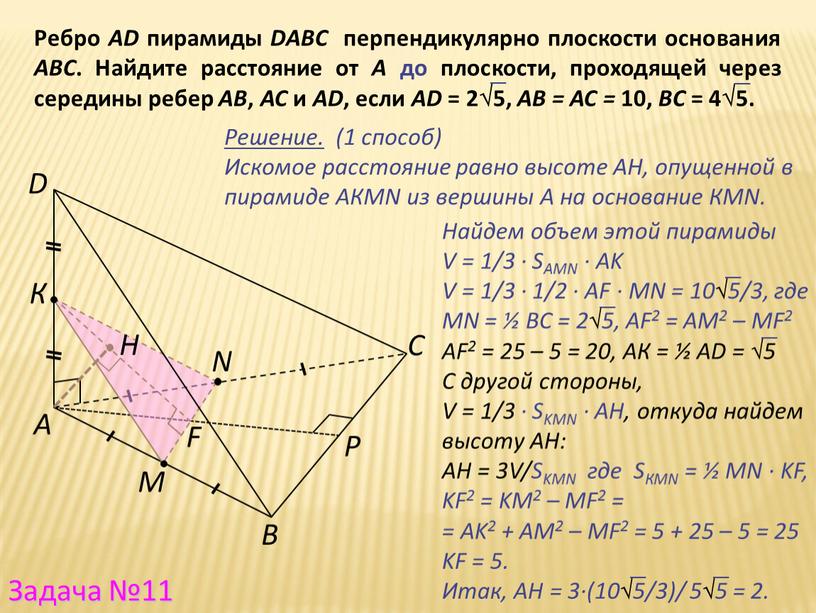
Решение. (1 способ)
Искомое расстояние равно высоте АН, опущенной в пирамиде АКМN из вершины А на основание КМN.

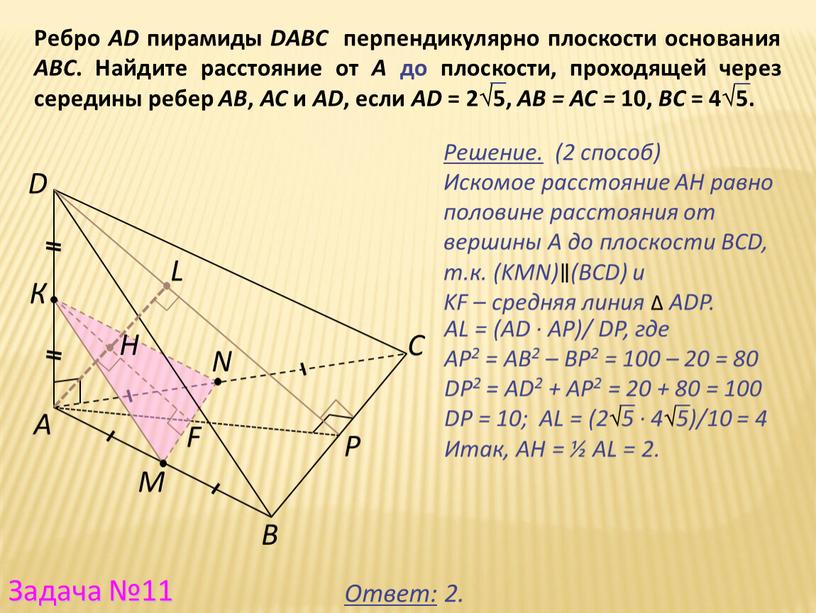
Ребро AD пирамиды DABC перпендикулярно плоскости основания

Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через середины ребер АВ, АС и АD, если АD = 25, АВ = АС = 10, ВС = 45.

Решение. (2 способ)
Искомое расстояние AH равно половине расстояния от вершины А до плоскости BCD, т.к. (KMN)∥(BCD) и
KF – средняя линия ∆ ADP.

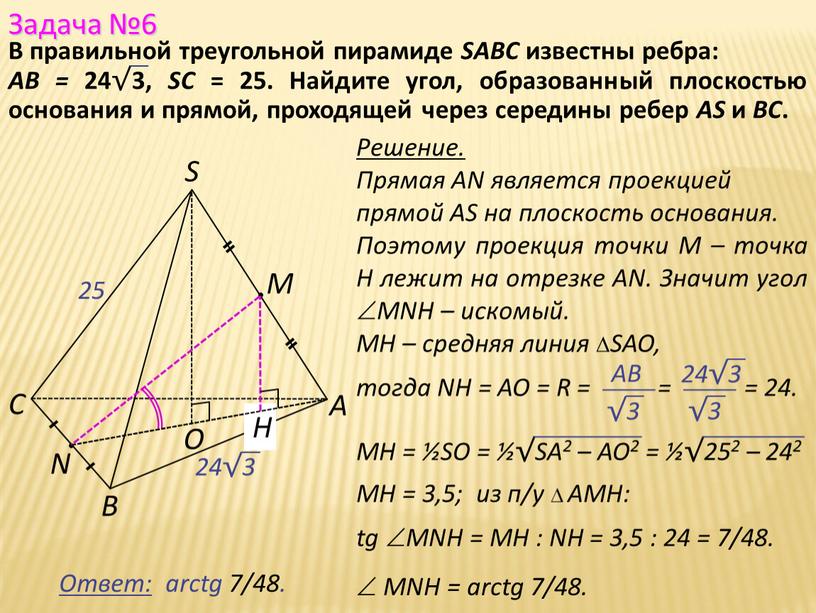
А С В D M N 10 6 В пирамиде DABC известны длины ребер:

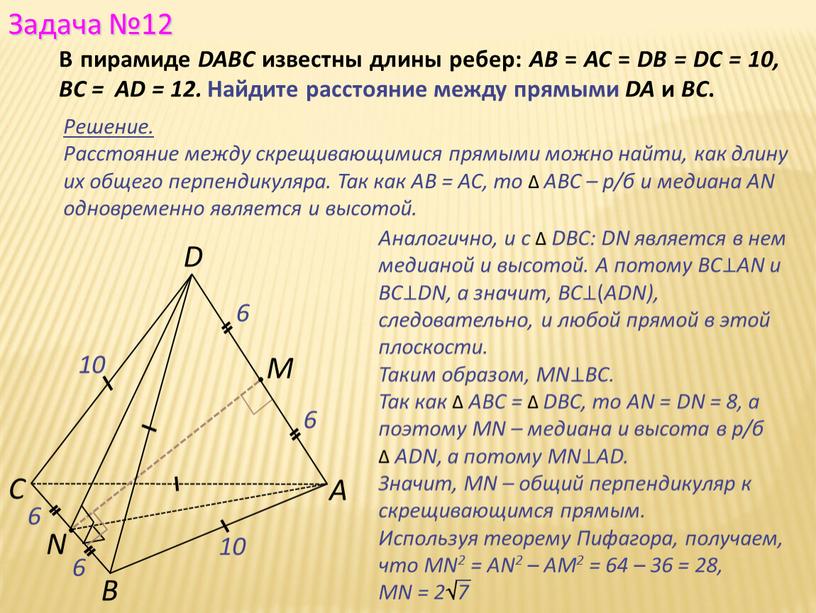
В пирамиде DABC известны длины ребер: АВ = АС = DВ = DС = 10, BC = АD = 12. Найдите расстояние между прямыми DA и ВС.

Аналогично, и с ∆ DBC: DN является в нем медианой и высотой. А потому ВС⊥АN и ВС⊥DN, а значит, ВС⊥(ADN), следовательно, и любой прямой в этой плоскости.
Таким образом, MN⊥ВС. Так как ∆ АВС = ∆ DBC, то АN = DN = 8, а поэтому MN – медиана и высота в р/б
∆ АDN, а потому MN⊥AD.
Значит, MN – общий перпендикуляр к скрещивающимся прямым.
Используя теорему Пифагора, получаем, что MN2 = AN2 – AM2 = 64 – 36 = 28,
MN = 27

Решение.
Расстояние между скрещивающимися прямыми можно найти, как длину их общего перпендикуляра. Так как АВ = АС, то ∆ АВС – р/б и медиана АN одновременно является и высотой.

В основании четырехугольной пирамиды

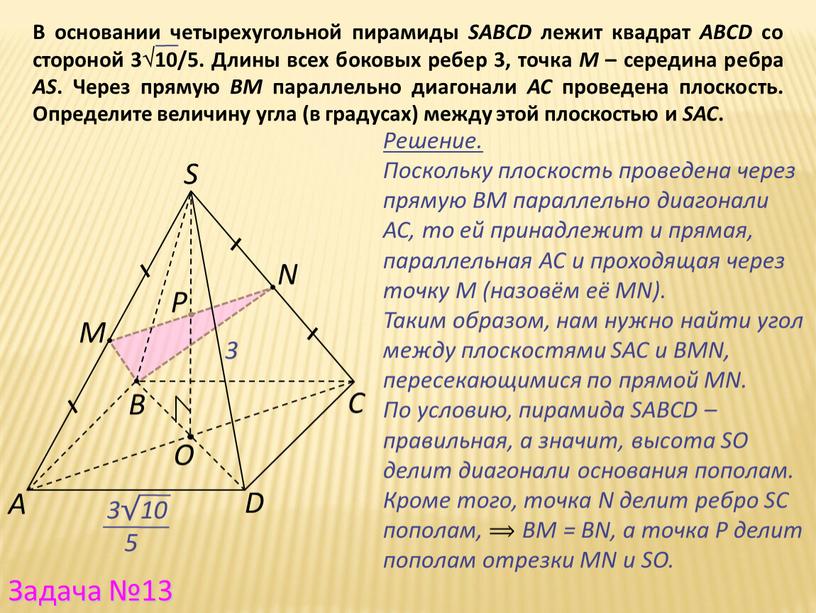
В основании четырехугольной пирамиды SАВСD лежит квадрат АВСD со стороной 310/5. Длины всех боковых ребер 3, точка М – середина ребра AS. Через прямую ВМ параллельно диагонали АС проведена плоскость. Определите величину угла (в градусах) между этой плоскостью и SAC.

Решение.
Поскольку плоскость проведена через прямую ВМ параллельно диагонали АС, то ей принадлежит и прямая, параллельная AC и проходящая через точку M (назовём её MN).
Таким образом, нам нужно найти угол между плоскостями SAC и BMN, пересекающимися по прямой MN.
По условию, пирамида SABCD – правильная, а значит, высота SO делит диагонали основания пополам.
Кроме того, точка N делит ребро SC пополам, ⟹ BM = BN, а точка P делит пополам отрезки MN и SO.

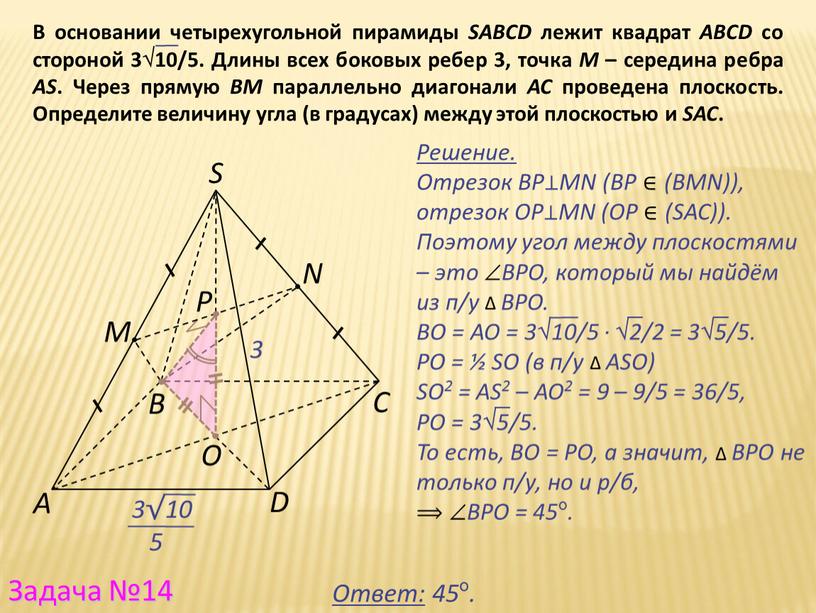
P Решение. Отрезок BP ⊥ MN (BP ∈ (BMN)), отрезок

Решение.
Отрезок BP⊥MN (BP ∈ (BMN)),
отрезок OP⊥MN (OP ∈ (SAC)).
Поэтому угол между плоскостями – это BPO, который мы найдём из п/у ∆ BPO.
BO = AO = 310/5 · 2/2 = 35/5. PO = ½ SO (в п/у ∆ ASO)
SO2 = AS2 – AO2 = 9 – 9/5 = 36/5,
PO = 35/5. То есть, BO = PO, а значит, ∆ BPO не только п/у, но и р/б,
⟹ BPO = 45º.

В основании четырехугольной пирамиды SАВСD лежит квадрат АВСD со стороной 310/5. Длины всех боковых ребер 3, точка М – середина ребра AS. Через прямую ВМ параллельно диагонали АС проведена плоскость. Определите величину угла (в градусах) между этой плоскостью и SAC.

Источник

В кубе abcda1b1c1d1 сторона основания равна 5 постройте линейный

В кубе ABCDA₁B₁C₁D₁ все рёбра равны 7. На его ребре BB₁ отмечена точка K так. что KB = 4. Через точки K и C₁ проведена плоскость α, параллельная прямой BD₁.

б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

а) Проведём через точку K прямую, параллельную BD₁. Пусть эта прямая пересекает плоскость грани A₁B₁C₁D₁ в точке L. Прямая KL лежит в плоскости BB₁D₁, значит, точка L лежит на диагонали B₁D₁. Более того,

Прямая C₁L пересекает ребро A₁B₁ в точке P, принадлежащей плоскости α.

Значит,

б) Объём куба ABCDA₁B₁C₁D₁ равен 343. Объём тетраэдра PKC₁B₁ равен одной шестой произведения его измерений:

Значит, объём оставшейся части равен

Ответ: б)

Источник

В кубе abcda1b1c1d1 сторона основания равна 5 постройте линейный

В правильной четырехугольной призме ABCDA₁B₁C₁D₁ стороны основания равны 4, боковые ребра равны 6. Точка M — середина ребра CC₁, на ребре BB₁ отмечена точка N, такая, что BN : NB₁ = 1 : 2.

а) Докажите, что плоскость AMN делит ребро DD₁ в отношении 1 : 5, считая от точки D.

б) Найдите угол между плоскостями ABC и AMN.

а) Пусть K — точка пересечения плоскости AMN с ребром DD₁. Заметим, что прямые AK и MN параллельны, прямые KM и AN параллельны. Проведём прямую NN₁ параллельно прямым BC и AD. Тогда углы KAD и MNN₁ равны, и треугольники AKD и NMN₁ равны. Далее имеем:

б) Продлим прямую MN до пересечения с прямой BC. Пусть E — точка их пересечения. Так как E лежит на обеих этих прямых, она лежит на прямой пересечения плоскостей ABC и AMN, следовательно, эти плоскости пересекаются по прямой AE. Из точки N на прямую AE опустим перпендикуляр BH. По теореме о трёх перпендикулярах его проекция BH также перпендикулярна AE. Таким образом, угол NHB — линейный угол двугранного угла между плоскостями ABC и AMN.

Имеем: тогда

Далее, EB = 8, тогда

Ответ: б)

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Источник Оцените статью Вам также может понравиться datchik-naruzhnoj-temperaturi-pezho-bokser-gde-naxodi-zpsn3use ����JFIF«��C (1#%(:3=Mqypdx\egc��C//cB8Bcccccccccccccccccccccccccccccccccccccccccccccccccc����» 0196 Датчик дроссельной заслонки 06681 для каких автомобилей 06681 датчик дроссельной заслонки для какого авто Датчик 0211 Где находится датчик заднего хода на ВАЗ 2112 с 16 клапанами? Ваз 2112 датчик заднего хода где находится 16 клапанов 0224 Где находится датчик давления топлива на двигателе 1jz fse: подробная инструкция Где находится датчик давления топлива 1jz fse Двигатель 0196 Расположение датчика положения коленвала в автомобиле Ford Mondeo Где находится датчик положения коленвала форд мондео 0230 Где находится датчик холостого хода на Приоре 16 клапанов с электропедалью? Где находится датчик холостого хода приора 16 клапанов 0262 Где расположены датчики подушек безопасности на Nissan Tiida? Где находятся датчики подушки безопасности ниссан тиида 0215 Датчик SAS в Volvo XC90: что это и как он работает Датчик sas volvo xc90 что это такое Система безопасности 0142 Adblock detector