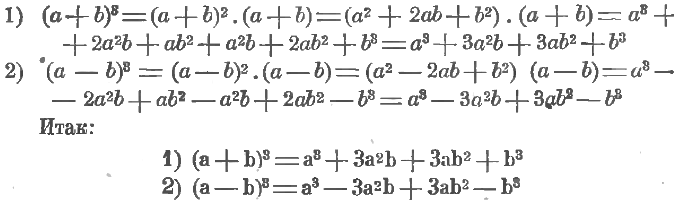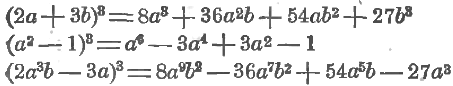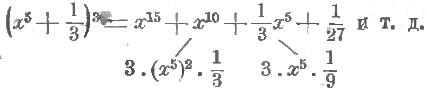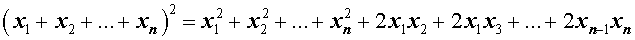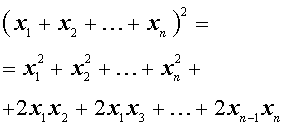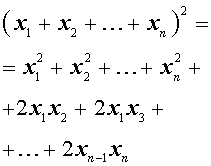Математика
Станем опять сначала на точку зрения арифметики и рассмотрим возведение в куб суммы и разности двух чисел. Получим:
Словами эти равенства читаются так:
1) Куб суммы двух чисел равняется кубу первого числа, плюс произведение тройки на квадрат первого числа и на второе число, плюс произведение тройки на первое число и на квадрат второго числа, плюс куб второго числа.
2) Куб разности двух числе равен кубу первого числа, минус произведение тройки на квадрат первого числа и на второе, плюс произведение тройки на первое число и на квадрат второго, минус куб второго числа.
Теперь мы можем сразу написать, что, например,
Здесь сначала написан куб первого числа, т. е. (2a 3 b) 3 , а это = 8a 9 b 3 , затем «минус произведение 2 на квадрат первого числа и на второе», т. е. –3 ∙ (2a³b)² ∙ (3a)= –3 ∙ 4a 6 b 2 ∙ 3a = – 36a 7 b 2 , затем «плюс произведение тройки на первое число и на квадрат второго», т. е. +3 ∙ (2a³b) ∙ (3a)² = +3 ∙ 2a3b ∙ 9a 2 = 54a 5 b, наконец, «минус куб второго числа», т. е. –(3a) 3 = –27a 3 .
Мы можем наши равенства переписать в виде:
Куб двучлена равен кубу первого члена, плюс произведение числа (+3) на квадрат первого члена и на второй, плюс произведение числа (+3) на первый член и на квадрат второго, плюс куб второго члена.
Например: (–3a 4 – ab) 3 = (–3a 4 ) 3 + (+3) (–3a 4 ) 2 (–ab) + (–3a 4 ) (–ab) 2 + (–ab) 3 = –27a 12 – 27a 9 b – 3a 5 b 2 – a 3 b 3 и т. п.
Если потребуется возвести в куб трехчлен, то можно или сводить дело к умножению
[Например: (x² – 2x – 1)³ = (x² – 2x – 1)(x² – 2x – 1)(x² – 2x – 1) = …]
или, приняв временно два члена (лучше первые два) за одно число, свести дело к возведению в куб двучлена:
Формулы сокращенного умножения:
сумма степеней и разность степеней
Формулы сокращенного умножения включают в себя следующие группы формул:
 | Степень суммы |
 | Степень разности |
 | Квадрат многочлена |
 | Куб трехчлена |
 | Сумма нечетных степеней |
 | Разность нечетных степеней |
 | Разность четных степеней |
Сумма нечетных степеней
Группа формул «Сумма нечетных степеней» приведена в Таблице 3.
Таблица 3. – Сумма нечетных степеней
| Название формулы | Формула |
| Сумма кубов | x 3 + y 3 = (x + y) (x 2 – xy + y 2 ) |
| Сумма пятых степеней | x 5 + y 5 = (x + y) (x 4 – x 3 y + x 2 y 2 – xy 3 + y 4 ) |
| Сумма седьмых степеней | x 7 + y 7 = (x + y) (x 6 – x 5 y + x 4 y 2 – x 3 y 3 + x 2 y 4 – xy 5 + y 6 ) |
| . | . |
| Сумма степеней порядка 2n + 1 | x 2n + 1 + y 2n + 1 = (x + y) (x 2n – x 2n – 1 y + x 2n – 2 y 2 – . – xy 2n – 1 + y 2n ) |
Сумма степеней порядка 2n + 1
| x 2n + 1 + y 2n + 1 = = (x + y) (x 2n – – x 2n – 1 y + + x 2n – 2 y 2 – – . – xy 2n – 1 + y 2n ) |
Разность нечетных степеней
Если в формулах из Таблицы 3 заменить y на – y , то мы получим группу формул «Разность нечетных степеней» (Таблица 4.):
Таблица 4. – Разность нечетных степеней
| Название формулы | Формула |
| Разность кубов | x 3 – y 3 = (x – y) (x 2 + xy + y 2 ) |
| Разность пятых степеней | x 5 – y 5 = (x – y) (x 4 + x 3 y + x 2 y 2 + xy 3 + y 4 ) |
| x 7 – y 7 = (x – y) (x 6 + x 5 y + x 4 y 2 + x 3 y 3 + x 2 y 4 + xy 5 + y 6 ) | |
| . | . |
| Разность степеней порядка 2n + 1 | x 2n + 1 – y 2n + 1 = (x – y) (x 2n + x 2n – 1 y + x 2n – 2 y 2 + . + xy 2n – 1 + y 2n ) |
Разность седьмых
степеней
Разность степеней порядка 2n + 1
| x 2n + 1 – y 2n + 1 = = (x – y) (x 2n + + x 2n – 1 y + + x 2n – 2 y 2 + + . + xy 2n – 1 + y 2n ) |
Разность четных степеней
Группа формул «Разность четных степеней» приведена в Таблице 5.
Таблица 5. – Разность четных степеней
| Название формулы | Формула | |
| Разность квадратов | x 2 – y 2 = (x + y) (x – y) | |
| Разность четвертых степеней |
| |
| Разность шестых степеней |
| |
| Разность восьмых степеней |
| |
| . | . | |
| Разность степеней порядка 2n | x 2n – y 2n = (x + y) (x 2n – 1 – x 2n – 2 y + x 2n – 3 y 2 – . + xy 2n – 2 – y 2n – 1 ) , x 2n – y 2n = (x – y) (x 2n – 1 + x 2n – 2 y + x 2n – 3 y 2 + . + xy 2n – 2 + y 2n – 1 ) |
Разность четвертых степеней
| x 4 – y 4 = = (x + y) (x 3 – x 2 y + + xy 2 – y 3 ) = = (x + y) (x – y) (x 2 + + y 2 ) |
| x 6 – y 6 = = (x + y) (x 5 – x 4 y + + x 3 y 2 – – x 2 y 3 + + xy 4 – y 5 ) = = (x + y) (x – y) (x 2 – – xy + y 2 ) (x 2 + + xy + y 2 ) |
Разность восьмых степеней
| x 8 – y 8 = = (x + y) (x 7 – x 6 y + + x 5 y 2 – x 4 y 3 + + x 3 y 4 – – x 2 y 5 + xy 6 – y 7 ) = = (x + y) (x – y) (x 2 + + y 2 ) (x 4 + y 4 ) |
Разность степеней порядка 2n
| x 2n – y 2n = = (x + y) (x 2n – 1 – – x 2n – 2 y + + x 2n – 3 y 2 – – . + xy 2n – 2 – – y 2n – 1 ) |
| x 2n – y 2n = = (x – y) (x 2n – 1 + + x 2n – 2 y + + x 2n – 3 y 2 + + . + xy 2n – 2 + + y 2n – 1 ) |
Замечание . Оба разложения на множители двучлена:
приведенные в последней строке Таблицы 5, можно продолжить и далее, по аналогии с тем, как это сделано в других строках таблицы.
Другие формулы сокращенного умножения можно посмотреть в разделе «Формулы сокращенного умножения: степень суммы, степень разности» нашего справочника.
Формулы сокращенного умножения:
степень суммы и степень разности
Формулы сокращенного умножения включают в себя следующие группы формул:
 | Степень суммы |
 | Степень разности |
 | Квадрат многочлена |
 | Куб трехчлена |
 | Сумма нечетных степеней |
 | Разность нечетных степеней |
 | Разность четных степеней |
Степень суммы
Группа формул «Степень суммы» составляет Таблицу 1. Эти формулы можно получить, выполняя вычисления в следующем порядке:
| (x + y) 2 = (x + y)(x + y) , (x + y) 3 = (x + y) 2 (x + y) , (x + y) 4 = (x + y) 3 (x + y) |
Группу формул «Степень суммы» можно получить также с помощью треугольника Паскаля и с помощью бинома Ньютона, которым посвящены специальные разделы нашего справочника.
| Название формулы | Формула |
| Квадрат (вторая степень) суммы | (x + y) 2 = x 2 + 2xy + y 2 |
| Куб (третья степень) суммы | (x + y) 3 = x 3 + 3x 2 y + 3xy 2 + y 3 |
| Четвертая степень суммы | (x + y) 4 = x 4 + 4x 3 y + 6x 2 y 2 + 4xy 3 + y 4 |
| Пятая степень суммы | (x + y) 5 = x 5 + 5x 4 y + 10x 3 y 2 + 10x 2 y 3 + 5xy 4 + y 5 |
| Шестая степень суммы | (x + y) 6 = x 6 + 6x 5 y + 15x 4 y 2 + 20x 3 y 3 + 15x 2 y 4 + 6xy 5 + y 6 |
| … | … |
Квадрат (вторая степень) суммы
Общая формула для вычисления суммы
с произвольным натуральным значением n рассматривается в разделе «Бином Ньютона» нашего справочника.
Степень разности
Если в формулах из Таблицы 1 заменить y на – y , то мы получим группу формул «Степень разности» (Таблица 2.):
Таблица 2. – Степень разности
| Название формулы | Формула |
| Квадрат (вторая степень) разности | (x – y) 2 = x 2 – 2xy + y 2 |
| Куб (третья степень) разности | (x – y) 3 = x 3 – 3x 2 y + 3xy 2 – y 3 |
| Четвертая степень разности | (x – y) 4 = x 4 – 4x 3 y + 6x 2 y 2 – 4xy 3 + y 4 |
| Пятая степень разности | (x – y) 5 = x 5 – 5x 4 y + 10x 3 y 2 – 10x 2 y 3 + 5xy 4 – y 5 |
| Шестая степень разности | (x – y) 6 = x 6 – 6x 5 y + 15x 4 y 2 – 20x 3 y 3 + 15x 2 y 4 – 6xy 5 + y 6 |
| … | … |
Квадрат (вторая степень) разности
Куб (третья степень) разности
Четвертая степень разности
Квадрат многочлена
Следующая формула применяется достаточно часто и называется «Квадрат многочлена» :
Словами эту формулу можно выразить так: — «Квадрат многочлена равен сумме квадратов всех его членов плюс сумма всевозможных удвоенных произведений его членов».
Куб трехчлена
Следующая формула называется «Куб трехчлена» :
Другие формулы сокращенного умножения приведены в разделе «Формулы сокращенного умножения: сумма степеней, разность степеней» нашего справочника.