Диагональное сечение куба: как найти его площадь, примеры, решение
Содержание:
Куб (правильный гексаэдр) – геометрическое тело, состоящее из шести попарно параллельных поверхностей и 12 одинаковых граней. Ещё ним называют правильный многогранник, основание коего – квадрат. Рассмотрим, как найти площадь диагонального сечения куба. После ознакомления с формулой решим пару несложных задач.
Диагональное сечение куба
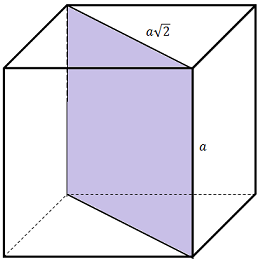
Секущая площадь куба имеет форму прямоугольника, где одна пара сторон представлена рёбрами кубика, вторая – диагоналями граней. Для вычисления её площади нужна только длина ребра правильного прямоугольника, ведь одна из них выполняет роль высоты. Длина диагонали для треугольников, где высота – это гипотенуза, а рёбра – катеты, определяется по формуле a*√2. Занимаемая диагональным сечением куба площадь равняется:
Задачи
Решение. Мы знаем, как вычислить площадь прямоугольника, который лежит в основании сечения, и двух боковых поверхностей тела.
Для боковой поверхности используем формулу: SБП = 2a2 – умножаем длину стороны саму на себя, затем – на два – количество сторон усечённого кубика.
Для прямоугольника SОСН = a * a√2 = a 2 *√2.
SПОЛН = SОСН + SБП = a 2 *√2 + 2a 2 = 202*√2 + 2 * 202 = 400*√2 + 800 = 1365,7 см 2 .
Вычислить поверхность куба, если его диагональное сечение равно 8 * √2 см 2 .
Необходимо вычислить размер грани правильного гексаэдра, затем – возвести в квадрат – для нахождения S одной поверхности, далее – умножить на их количество – шесть штук.
Возьмём длину ребра, равную a; величины его поверхности – a 2 ; полная поверхность – 6a 2 .
Форма сечения гексаэдра с равными гранями – прямоугольник, где пара сторон – ребра квадрата, вторая – диагонали оснований. Из формулы они равны a√2. Подставим значения:
S = a 2 *√2. Длина грани рассматриваемого куба: a = √8, площадь одной грани – √8 2 = 8, а полная равна её произведению на количество сторон: SП = 6 * 8 = 48 см 2 .
Для проведения более сложных расчётов часто придётся задействовать теорему Пифагора.
Две задачи на построение сечений
Здесь рассмотрено подробное решение двух наиболее сложных, на мой взгляд, задач из представленных в группе Задачи на построение сечений многогранников на этом сайте. Если Вы еще не выполняли подобных заданий, вернитесь на указанную страницу и попробуйте поработать самостоятельно.
Задача 6.
Замечание: куб на чертеже может быть повёрнут к нам любой гранью, но трудно предугадать, какой удобнее для построения. Поэтому, если совсем не получается решение какой-либо задачи по стереометрии, то я рекомендую начинать заново, перерисовав исходный чертёж. А зачастую бывает достаточно просто переставить символы, обозначающие вершины основания многоугольника (естественно, не произвольно, а согласовав между собой и с условием задачи).
Для начала вспомним признак перпендикулярности прямой и плоскости.
Теорема. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения, то она перпендикулярна плоскости.
Аксиома. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Поэтому для реализации нашей цели нужно найти две различные плоскости, содержащие прямую B1D, и построить в них нужные перпендикуляры. В качестве таковых в кубе можно взять, например, плоскости B1BDD1 и B1ADC1
Построим сечение B1BDD1. Две противоположные стороны этого четырёхугольника являются рёбрами куба, а две другие — диагоналями его граней. По свойствам куба можем сделать вывод, что B1BDD1 – прямоугольник длина которого в √2 _ раз больше ширины. Делим диагональ на 4 части и ставим точку К, удовлетворяющую условию B1K : B1D = 1 : 4. Проводим через эту точку перпендикуляр к B1D. Отрезок MN лежит на одной из искомых прямых.
При необходимости легко уточнить положение точек M и N на поверхности куба. Если задана длина ребра (или можно обозначить её, например, символом a), то длины отрезков B1M и B1N легко вычисляются из подобия прямоугольных треугольников, которое хорошо просматривается на плоском чертеже.
Получили четыре точки, принадлежащие искомой плоскости сечения и поверхности куба. Соединяем прямой линией точки M и F на грани BСС1B1. Соединяем точки F и N на грани A1B1С1D1 и продолжаем прямую до пересечения с ребром A1B1 в точке R. Соединяем точки R и E на грани A1B1BA и продолжаем прямую до пересечения с ребром B1B в точке. M ? Но где гарантия, что именно в точке M, а не выше или ниже по ребру?
Если были проведены вычисления отрезков B1F = B1M и B1N = B1E в процессе анализа плоских прямоугольников, то ответ становится очевидным: так как прямоугольные треугольники B1RF, B1RM и B1FM равнобедренные и равные.
Если же при построении положение точек M и F не вычислялось, а контролировался только факт их положения на рёбрах куба, то придётся произвести ряд вычислений на этапе доказательства верности построения.
Замечание I.
Возможен альтернативный подход к этой задаче. Так как куб является правильным многогранником и имеет центр симметрии, расположенный в точке пересечения диагоналей, а значит на линии B1D, с которой мы работаем, то можно предположить, что сечение также будет симметричным и будет иметь форму равностороннего треугольника. Поэтому после анализа (жёлтого) прямоугольника на первом чертеже и получения точки М, можно сразу отложить от вершины B1 на рёбрах куба равные отрезки B1R = B1F = B1M, а затем доказать, что плоскость RMF перпендикулярна прямой B1D. Для этого лучше всего воспользоваться теоремой о трёх перпендикулярах.
Теорема. Прямая, проведенная на плоскости через основание наклонной перпендикулярно её проекции, перпендикулярна и самой наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Замечание II.
Вид сечения сильно зависит от положения точки K на диагонали куба. Попробуйте сместить точку K ближе к середине отрезка B1D и построить MN ⊥ B1D в прямоугольнике B1BDD1. На каких гранях и рёбрах куба теперь окажутся точки искомого сечения?
Ниже вы можете посмотреть маленькое видео о том, как изменяется сечение куба плоскостью, перпендикулярной его диагонали, в зависимости от положения их точки пересечения.
Задача 16.
При решении задачи предполагаем, что все операции на плоскости, в частности, построение параллельных и перпендикулярных прямых, нам известны из планиметрии и в подробном описании не нуждаются.
Чтобы построить плоскость, параллельную заданной плоскости, нужно вспомнить признак параллельности двух плоскостей.
Теорема. Две плоскости параллельны, если одна из них параллельна двум пересекающимся прямым, лежащим в другой плоскости.
Теорема. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Кроме того, нам нужно, чтобы плоскость сечения проходила через заданную точку А2. Значит, хорошо бы сразу найти две такие пересекающиеся прямые, параллельные каким-либо прямым в плоскости PQR, чтобы хотя бы одна из них содержала точку А2. В этом и будет состоять первый этап решения задачи.
Через точки R и Р проводим РN || CC1 и RM || CC1 . Соединяем точки M и N прямой линией. По свойствам призмы получим MN || RР и MN = RР .
Терерь рассмотрим диагональное сечение призмы, проведенное через параллельные прямые AA1 и СС1. Плоскость AA1C1C содержит заданные точкии A2 и Q и пересекает заданную плоскость PQR по линии QE. (Буквой Е обозначена общая точка линии пересечения плоскостей и прямой RP.) В этой плоскости (голубой на чертеже) через точку А2 проводим прямую, параллельную QE до пересечения с верхним основанием призмы в точке F. А2F || QE по построению.
На верхней грани призмы через точку F проводим прямую, параллельную линии MN, которая в нашем случае пересекает рёбра призмы A1D1 и B1C1 в точках H и G соответственно. HG || MN .
В зависимости от положения точки А2 на ребре АА1 положение точек H и G на рёбрах призмы может изменяться. Например, если бы точка А2 располагалась ближе к вершине А1, то точка G могла бы оказаться на ребре А1В1, а если бы она находилась близко к вершине А, то точка Н могла бы оказаться на ребре D1С1. От этого зависит окончательная форма искомого сечения призмы. Т.е. поскольку в условии задачи положение точек на рёбрах не фиксировано, то ваши ответы могут отличаться от приведенного мной не только формой на чертеже, но и количеством сторон получившегося многоугольника.
Обе прямые HG и RР параллельны прямой MN по построению, следовательно HG || RР . Для прямых в плоскости это вам уже известно давно. Для прямых в пространстве это тоже доказано.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
Таким образом, прямые А2F и HG и есть те самые прямые, которые мы искали. А2F параллельна QE, следовательно параллельна плоскости PQR. HG параллельна RР, следовательно параллельна плоскости PQR. А2F и HG пересекаются в точке F. Эти прямые определят секущую плоскость, параллельную заданной PQR.
Аксиома. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Продолжим прямую HG до пересечения с ребром A1B1 в точке L. Точка L принадлежит верхней и фронтальной (на нашем чертеже) граням призмы, поскольку она принадлежит их общему ребру. Кроме того, точка L принадлежит плоскости сечения, поскольку находится на прямой HG. Следовательно, эта точка должна принадлежать и линии пересечения фронтальной грани с плоскостью сечения. Соединяем точку L с точкой А2. Эта прямая будет принадлежать плоскости грани АА1В1В на основании следующей теоремы.
Теорема. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Пользуясь этим же утверждением, соединяем и остальные две пары точек, принадлежащих одной грани призмы.
То, что оно удовлетворяет условию проходить через точку А2 очевидно по построению. То, что плоскость A2HGK параллельна плоскости RQP мы доказали, ссылаясь на соответствующие положения теории на каждом шаге построения.
Замечание.
Конечно, во время экзамена вы не будете делать несколько чертежей и так подробно описывать построение. Итоговый чертёж будет выглядеть примерно так.
Однако, не забывайте, что основное требование к заданиям второй части ЕГЭ профильного уровня это обоснованность решения. Поэтому, если вы просто выполнили все построения и представили на проверку итоговый чертёж, то к нему необходимо написать доказательство, которое содержит ссылки на теорию. При этом не обязательно цитировать теоремы полностью, можно упомянуть их названия.
Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.
Понравились материалы сайта?
Узнайте, как поддержать сайт и помочь его развитию.
Есть вопросы? пожелания? замечания? Обращайтесь — mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.