- Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников
- Расстояние от точки до плоскости (ЕГЭ 2022)
- Расстояние от точки до плоскости — коротко о главном
- Расстояние от точки до плоскости
- Способы нахождения расстояния от точки до плоскости
- Геометрический способ
- Нахождение расстояния от точки до плоскости. 11-й класс
- Презентация к уроку
Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников
Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов
14(C2). Найти расстояние от середины ребра куба до плоскости сечения куба (вар. 55)
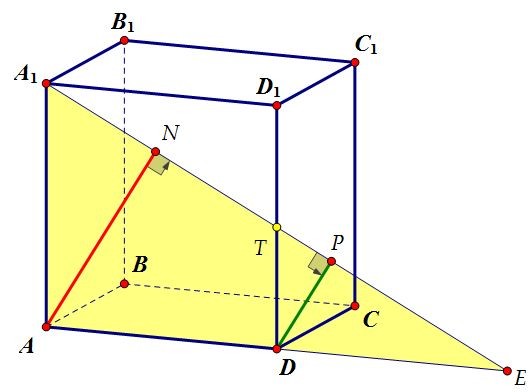
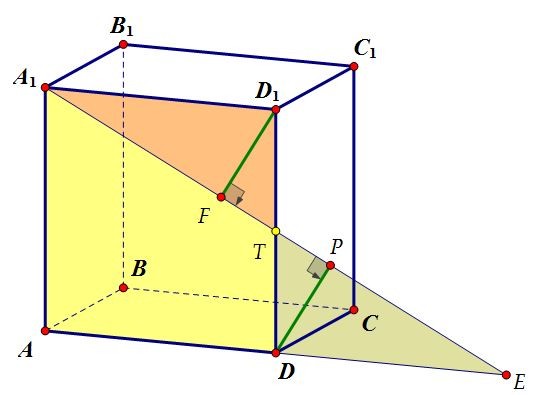
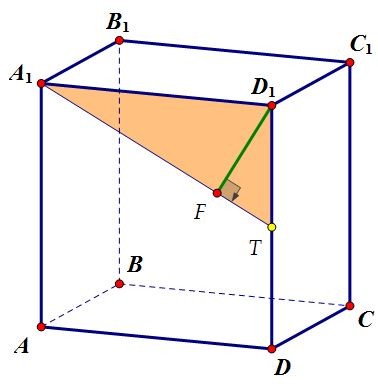
В кубе ABCDA1B1C1D1 плоскость проходит через прямую A1B1 и середину ребра DD1. Найти расстояние от середины ребра CD до плоскости, если ребро куба равно 4.
Построить плоскость сечения просто. Достаточно через точку Т — середину ребра DD1 провести в плоскости DD1C1C прямую ТК параллельно A1B1 (точка К — середина СС1). Сечение обязательно пересечёт параллельные грани по параллельным прямым.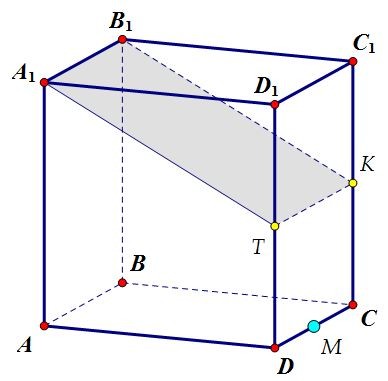 
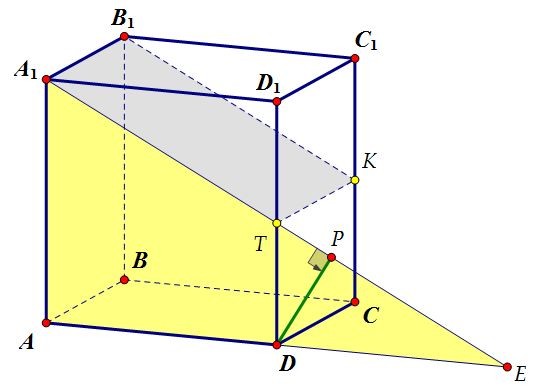
CD параллельна плоскости сечения по признаку параллельности прямой и плоскости. Расстояния от всех точек прямой CD (в том числе и от точки М — середины отрезка CD) до плоскости сечения одинаковы. Удобнее искать расстояние до сечения от точки D. 
Т.к. точка D лежит в плоскости AA1D1D, перпендикулярной сечению, значит, расстояние от точки D до плоскости сечения — это расстояние от точки D до прямой А1Т, по которой пересекаются перпендикулярные плоскости, т.е. отрезок DP, перпендикулярный А1Е. (докажите, что DP ⊥ А1В1КТ по признаку перпендикулярности прямой и плоскости). Длину DP можно искать из подобия треугольников DPЕ и А1АЕ. Но можно ещё проще: 
Треугольники DТЕ и D1ТА1 равны. Значит, равны и их соответствующие высоты. Будем искать высоту D1F треугольника D1ТА1, опущенную на гипотенузу А1Т. 
D1А1 = 4, D1Т = 2, А1Т = √ 4 2 + 2 2 = √ 20 = 2√ 5 Площадь прямоугольного треугольника можно искать двумя разными способами. SD1ТА1 = 0,5 · D1А1 · D1Т = 0,5 · А1T · D1F SD1ТА1 = 0,5 · 4 · 2 = 0,5 · 2√ 5 · D1F Можно искать высоту и в жёлтом треугольнике АА1Е, а затем разделить её на два. 
Автор: Ольга Себедаш Просмотров: 13172
Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов
Комментарии к этой задаче:
Комментарий добавил(а): Татьяна
Дата: 2014-01-06
Эту задачу можно решить методом координат,найдя уравнение плоскости (В1А1Т)и используя формулу расстояния от точки до плоскости.
Расстояние от точки до плоскости (ЕГЭ 2022)
Стереометрия выглядит жутко… Вернее, сама-то стереометрия красивая!
Знаю, что, когда на уроках скучно, все мы любим порисовать на полях кубы и объемные рисунки 🙂
А вот задачи по стереометрии жутковатые. Однако, если в них хорошо разобраться, все будет легко!
Давай начнем с базы – с расстояния от точки до плоскости.
Расстояние от точки до плоскости — коротко о главном
Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость.
Существует два способа найти расстояние от точки до плоскости:
Плюсы и минусы обоих способов:
| + | — | |
| АЛГ | Не нужно думать, можно просто применить несколько формул и стандартную процедуру. | Формулы громоздкие, их сложно запомнить, легко допустить ошибку. Особенно если система координат введена неудачно. |
| ГЕО | Не нужно запоминать длинных формул, вычисления обычно не длинные, арифметической ошибке трудно вкрасться. | Нужно уметь применять стереометрические теоремы и понимать, что такое доказательство. |
При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно:
- Ввести систему координат;
- Найти координаты точки и уравнение плоскости;
- Применить формулу расстояния от точки до плоскости (Формулу Герона).
\( \displaystyle \rho =\frac<|<_<<
\( \displaystyle \rho \)— искомое расстояние
\( \displaystyle \left( <
При геометрическом способе нужно:
- Построить перпендикуляр от точки до плоскости;
- Найти точку пересечения перпендикуляра с плоскостью;
- Выполнить необходимое дополнительное построение;
- Определяется расстояние от точки до точки, используя необходимые геометрические теоремы (по ситуации).
Расстояние от точки до плоскости
Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость.
Способы нахождения расстояния от точки до плоскости
Существует, по крайней мере, два способа найти расстояние от точки до плоскости: геометрический и алгебраический.
При геометрическом способе нужно сначала понять, как расположен перпендикуляр из точки на плоскость: может он лежит в какой –то удобной плоскости, является высотой в какой-нибудь удобном (или не очень) треугольнике, а может этот перпендикуляр вообще является высотой в какой-нибудь пирамиде.
После этого первого и самого сложного этапа задача распадается на несколько конкретных планиметрических задач (быть может, в разных плоскостях).
При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно ввести систему координат, найти координаты точки и уравнение плоскости, и после этого применить формулу расстояния от точки до плоскости.
Кажется с первого взгляда, что алгебраический способ легче, но это… далеко не всегда так. Проблемы обычно возникают как раз с нахождением координат точки и управления плоскости, особенно если система координат была введена не самым удобным способом. Для удобства приведём плюсы и минусы обоих способов в табличке:
| + | — | |
| АЛГ | Не нужно думать, можно просто применить несколько формул и стандартную процедуру. | Формулы громоздкие, их сложно запомнить, легко допустить ошибку. Особенно если система координат введена неудачно. |
| ГЕО | Не нужно запоминать длинных формул, вычисления обычно не длинные, арифметической ошибке трудно вкрасться. | Нужно уметь применять стереометрические теоремы и понимать, что такое доказательство |
Сейчас мы разберём один достаточно хитрый пример, двумя способами.
Задача: в кубе \( \text
Геометрический способ
Куда же опускается перпендикуляр из точки \( \displaystyle C\) на плоскость \( \displaystyle A<_<1>>M\)?
Смотрим на \( \displaystyle \Delta A<_<1>>M\) – оказывается, он равнобедренный – \( \displaystyle <_<1>>M=AM\)!
Проведём \( \displaystyle CA\) и \( \displaystyle C<_<1>>\). Зачем? А они тоже равны \( \displaystyle CA\) и \( \displaystyle C<_<1>>\).
Отметим точку \( \displaystyle K\) — середину \( \displaystyle A<_<1>>\) — и проведём \( \displaystyle MK\) и \( \displaystyle CK\). Треугольники \( \displaystyle A<_<1>>M\) и \( \displaystyle A<_<1>>C\) — равнобедренные, поэтому \( \displaystyle MK\bot A<_<1>>\) и \( \displaystyle CK\bot A<_<1>>\).
И вот теперь! Стереометрическая теорема идёт в ход: признак перпендикулярности прямой и плоскости.
Остался один шаг: проведём \( \displaystyle CH\bot MK\) (в плоскости \( \displaystyle CMK\), естественно).
Что же можно сказать о \( \displaystyle CH\)?
\( \displaystyle CH\bot MK\) по построению
\( \displaystyle CH\bot A<_<1>>\) – так как \( \displaystyle A<_<1>>\bot CMK\) и значит, \( \displaystyle A<_<1>>\) перпендикулярна всякой прямой в плоскости \( \displaystyle CMK\), в частности и \( \displaystyle CH\).
\( \displaystyle \left\< \begin
Искомый перпендикуляр из точки \( \displaystyle C\) на плоскость \( \displaystyle A<_<1>>M\) — это высота в \( \displaystyle \Delta CMK\). Осталось найти эту высоту.
Теперь площадь \( \displaystyle \Delta KCM\) по формуле Герона:
Нахождение расстояния от точки до плоскости. 11-й класс
Презентация к уроку
Цели:
- обобщение и систематизация знаний и умений учащихся;
- развитие умений анализировать, сравнивать, делать выводы.
Оборудование:
- мультимедийный проектор;
- компьютер;
- листы с текстами задач
I. Организационный момент
II. Этап актуализации знаний (слайд 2)
Повторяем как определяется расстояние от точки до плоскости
III. Лекция (cлайды 3-15)
На занятии мы рассмотрим различные способы нахождения расстояния от точки до плоскости.
Первый метод: поэтапно-вычислительный
Расстояние от точки М до плоскости α:
– равно расстоянию до плоскости α от произвольной точки Р, лежащей на прямой a, которая проходит через точку М и параллельна плоскости α;
– равно расстоянию до плоскости α от произвольной точки Р, лежащей на плоскости β, которая проходит через точку М и параллельна плоскости α.
№1. В кубе А…D1 найти расстояние от точки С1 до плоскости АВ1С.
Осталось вычислить значение длины отрезка О1Н.
№2. В правильной шестиугольной призме А…F1, все ребра которой равны 1, найдите расстояние от точки А до плоскости DEA1.
Следующий метод: метод объемов.
Если объем пирамиды АВСМ равен V, то расстояние от точки М до плоскости α, содержащей ∆АВС вычисляется по формуле ρ(М; α) = ρ(М; АВС) = 
При решении задач мы используем равенство объемов одной фигуры, выраженные двумя различными способами.
№3. Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через середины ребер АВ, АС и АD, если .
При решении задач координатным методом расстояние от точки М до плоскости α можно вычислить по формуле ρ(М; α) = 
, где М(х0; у0; z0), а плоскость задана уравнением ax + by + cz + d = 0
№4. В единичном кубе A…D1 найдите расстояние от точки А1 до плоскости ВDC1.
Введем систему координат с началом в точке А , ось у пройдет по ребру АВ, ось х – по ребру АD, ось z – по ребру АА1. Тогда координаты точек В (0; 1; 0) D (1; 0; 0;) C1(1; 1; 1)
Составим уравнение плоскости, проходящей через точки В, D, C1.
Тогда – dx – dy + dz + d = 0 x + y – z – 1= 0. Следовательно, ρ = 
Следующий метод, который можно использовать при решении задач данного типа – метод опорных задач.
Применение данного метода состоит в применении известных опорных задач, которые формулируются как теоремы.
№5. В единичном кубе А…D1 найдите расстояние от точки D1 до плоскости АВ1С.
Рассмотрим применение векторного метода.
№6. В единичном кубе А…D1 найдите расстояние от точки А1 до плоскости ВDС1.
Итак, мы рассмотрели различные способы, которые можно использовать при решении данного типа задач. Выбор того или иного метода зависит от конкретной задачи и ваших предпочтений.
IV. Работа в группах
Попробуйте решить задачу разными способами.
№1. Ребро куба А…D1 равно 
. Найдите расстояние от вершины С до плоскости BDC1.
№2. В правильном тетраэдре АВСD с ребром 
найдите расстояние от точки А до плоскости BDC
№3. В правильной треугольной призме АВСА1В1С1 все ребра которой равны 1, найдите расстояние от А до плоскости ВСА1.
№4. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от А до плоскости SCD.
V. Итог урока, домашнее задание, рефлексия