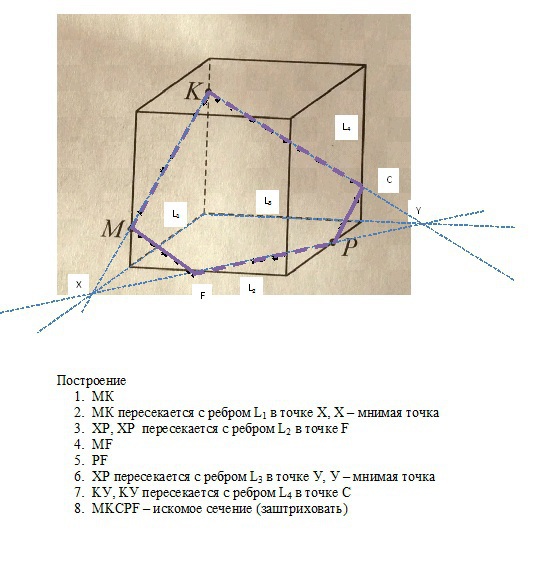
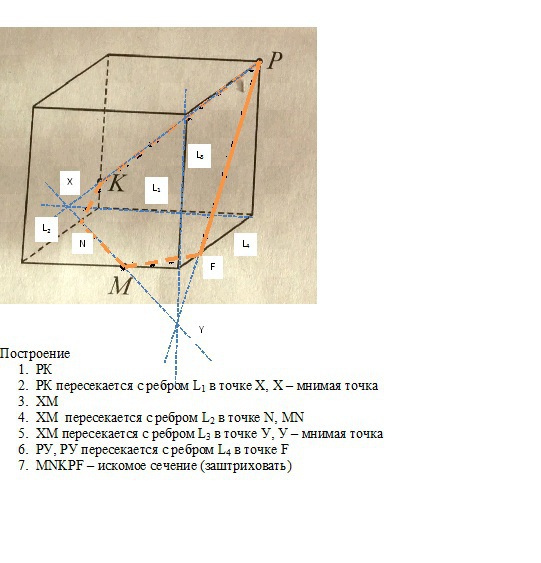
- Постройте сечение куба плоскостью мпр методом следа
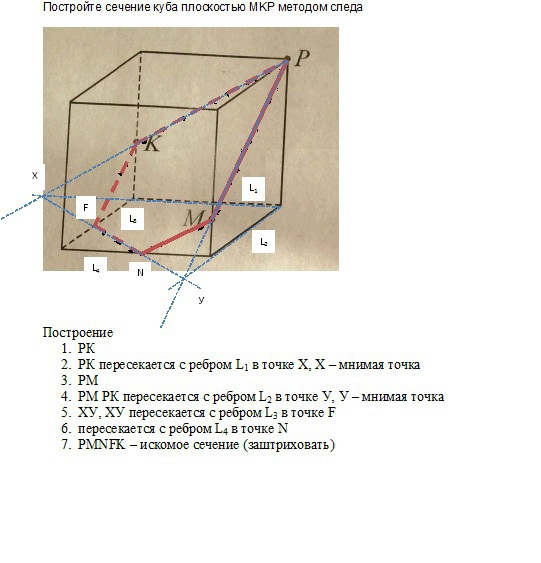
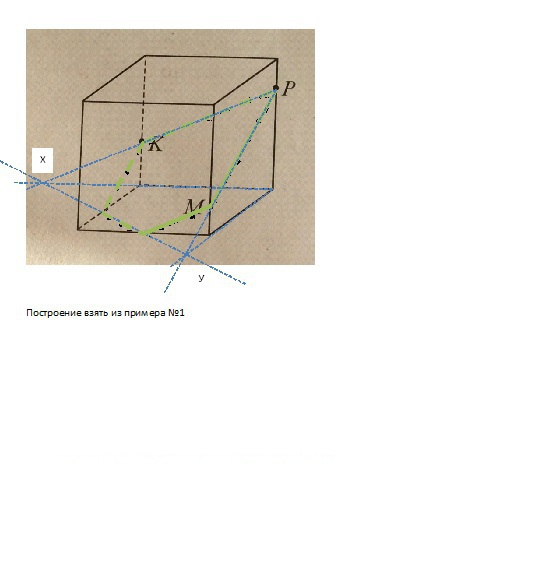
- Постройте сечение куба плоскостью MKP методом следа?
- Постройте сечение многогранника плоскостью?
- Отметьте точки M, K, P на рёбрах A1B1, BC, DD1 параллелепипеда ABCDA1B1C1D1?
- Постройте сечение куба плоскостью, проходящей через середину его ребра перпендикулярно к этому ребру?
- ПОМОГИТЕ пожалуйста решить?
- Постройте сечение куба abcda1b1c1d1 плоскостью проходящей через середины ребер ab bb1 b1c1?
- Дано изображение куба ABCDA1B1C1D1 а) постройте отрезок, который является пересечением грани DD1CC1 и плоскости α б) постройте сечение куба плоскостью α в) вычислите периметр построенного сечения, есл?
- Ребро куба АВСDA1B1C1D1 равно 24 см?
- Точка K — середина ребра A1D1 куба ABCDA1B1C1D1?
- Постройте сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки A, B и D₁?
- Точка м — середина ребра ав куба авсда1в1с1д1 ?
- Постройте сечение куба плоскостью мпр методом следа
- Как написать хороший ответ?
- Презентация «Метод следов»
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
Постройте сечение куба плоскостью мпр методом следа
Следом называют прямую пересечения плоскости сечения и плоскости какой-либо грани многогранника. Чтобы построить след, достаточно знать две его точки, т. е. точки, лежащие одновременно в секущей плоскости и плоскости рассматриваемой грани.
Основные правила построения сечений методом следа:
- Если даны (или уже построены) две точки плоскости сечения на одной грани многогранника, то след сечения этой плоскости – прямая, проходящая через эти три точки.
- Если дана (или уже построена) прямая пересечения плоскости сечения с основанием многогранника (след на основании) и есть точка, принадлежащая определенной боковой грани, то нужно определить точку пересечения данного следа с этой боковой гранью ( точка пересечения данного следа с общей прямой основания и данной боковой грани)
- Точку пересечения плоскости сечения с основанием можно определить как точку пересечения какой-либо прямой в плоскости сечения с ее проекцией на плоскость основания.
То есть, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры.
Для тех, кто знаком с гомологией, удобно ее применять при нахождении образов точек нижнего основания фигуры F – изображения фигуры. Последовательно соединяя образы этих точек, получим изображение искомого сечения.
В дальнейшем будем допускать вольность речи и говорить «строим сечение» вместо «строим изображение сечения».
M ϵ BB 1 , N ϵ CC 1 D 1 D , K ϵ AA 1 E . В данном случае очевидно, что М1 = В1 .
3. XY =s – след секущей плоскости
AMCDE — искомое сечение
Пример 2
Постройте сечение куба плоскостью MKP методом следа?
Постройте сечение куба плоскостью MKP методом следа.
Постройте сечение многогранника плоскостью?
Постройте сечение многогранника плоскостью.
Отметьте точки M, K, P на рёбрах A1B1, BC, DD1 параллелепипеда ABCDA1B1C1D1?
Отметьте точки M, K, P на рёбрах A1B1, BC, DD1 параллелепипеда ABCDA1B1C1D1.
Постройте сечение плоскостью MKP /
Заранее спасибо(рисунок обязательно).
Постройте сечение куба плоскостью, проходящей через середину его ребра перпендикулярно к этому ребру?
Постройте сечение куба плоскостью, проходящей через середину его ребра перпендикулярно к этому ребру.
ПОМОГИТЕ пожалуйста решить?
ПОМОГИТЕ пожалуйста решить!
1. Постройте сечение тетраэдра ABCD плоскостью проходящей через точки A, E, F, если точки E, F принадлежат рёбрам DB BC соответственно.
2. Постройте сечение куба ABCDA1B1C1D1 плоскость, проходящей через ребра AB и C1D1.
Какая фигура получилась в сечении?
3. В кубе ABCDA1B1C1D1 проведите сечение плоскостью через ребро CC1 и прямую, проходящую через точку пересечения диагоналей грани AA1DD1.
4. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью ABC1.
Постройте сечение куба abcda1b1c1d1 плоскостью проходящей через середины ребер ab bb1 b1c1?
Постройте сечение куба abcda1b1c1d1 плоскостью проходящей через середины ребер ab bb1 b1c1.
Дано изображение куба ABCDA1B1C1D1 а) постройте отрезок, который является пересечением грани DD1CC1 и плоскости α б) постройте сечение куба плоскостью α в) вычислите периметр построенного сечения, есл?
Дано изображение куба ABCDA1B1C1D1 а) постройте отрезок, который является пересечением грани DD1CC1 и плоскости α б) постройте сечение куба плоскостью α в) вычислите периметр построенного сечения, если известно, что ребро куба равно 6 см и то, что в плоскости α лежат прямая BB1 и точка M — середина D1C1.
Ребро куба АВСDA1B1C1D1 равно 24 см?
Ребро куба АВСDA1B1C1D1 равно 24 см.
Точка К — середина ребра ВВ1.
Через К проведена плоскость альфа, параллельная плоскости ВС1А1.
1)Постройте отрезок, который лежит в плоскости альфа и в грани АВВ1А1 ; 2)Постройте сечение куба плоскостью альфа.
; 3)Вычислите площадь сечения.
Точка K — середина ребра A1D1 куба ABCDA1B1C1D1?
Точка K — середина ребра A1D1 куба ABCDA1B1C1D1.
Постройте сечение куба плоскостью, проходящей через точку K и параллельно плоскости (AA1B1).
Вычислите площадь этого сечения, если длина ребра куба равна 3см.
Постройте сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки A, B и D₁?
Постройте сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки A, B и D₁.
Точка м — середина ребра ав куба авсда1в1с1д1 ?
Точка м — середина ребра ав куба авсда1в1с1д1 .
Постройте сечение куба плоскостью проходящей через точку м и параллельной плоскости вв1с1 .
ВЫЧИСЛИТЕ ПЛОЩАДЬ ЭТОГО СЕЧЕНИЯ ЕСЛИ АВ = 2см.
Если вам необходимо получить ответ на вопрос Постройте сечение куба плоскостью MKP методом следа?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.
Дано : ABCD — параллелограмм, AC и BD — диагонали, AC = BD. Доказать : ABCD — прямоугольник. Доказательство : 1. Рассмотрим треугольники ABD и DCA (не забываем, что важноправильно назвать треугольники! ). 1) AC = BD (по условию). 2) Сторона AD —..
Если боковая сторона к примеру в 3 раза больше, то х — основание, тогда две боковые стороны будут по 3х . Периметр равнобедренного треугольника равен 42 см. То есть все стороны надо сложить. Р = х + 3х + 3х42 = 7хх = 42 / 7 = 6 см основание, 6 * 3..
13. 9 — 6. 9 = 7 7 — отрезок BC так как AC — длина всего отрезка а AB 1 часть.
13, 9 — 6, 9 = 7 см отрезок ВС.
OA — луч ED — прямая JH — отрезок CF — прямая IB — луч OJ — отрезок JG — луч.
1. Площадь треугольника найдем по формуле Герона Полупериметр р = 0, 5(6 + 10 + 8) = 12 см. S = √12(12 — 6)(12 — 10)(12 — 8) = 24 см² S = 0, 5·p·r 0, 5·12·r = 24 r = 4 см ⇄.
Обозначим угол BAD через х, тогда угол CAE тоже равен х (так как BAD = CAE). Теперь обозначим угол BAC через y. Так как углы BAC и CAD в сумме дают угол BAD, то CAD = BAD — BAC = x — y. Итак, угол CAD равен x — y. Так как углы CAD и DAE в сумме д..
MM1, NN1, AA1, CC1 — перпендикуляры к BD. Треугольники MOM1 и NON1 равны (прямоугольные т. С равными гипотенузами и острыми углами) = > MM1 = NN1. MM1 и NN1 — средние линии в треугольниках BCC1 и DAA1 (MM1 || CC1, M — середина BC ; NN1 || AA1, N -..
А = 15 см, х = 20 см, hₐ = 4 см. Hₓ = ? Площадь параллелограмма равна произведению стороны на высоту, проведённую к ней. S = ahₐ = xhₓ, hₓ = ahₐ / x = 15·4 / 20 = 3 см — это ответ.
∆АСВ — прямоугольный cosB = CB / AB = 21 / 75 = 7 / 25 По основному тригонометрическому тождеству sinB = ✓(1 — (7 / 25)²) = ✓(1 — 49 / 625) = ✓576 / 625 = 24 / 25 ∆HCB — прямоугольный sinB = CH / CB = > CH = CB * sinB CH = 21 * 24 / 25 = 20, 16.
Постройте сечение куба плоскостью мпр методом следа
Постройте сечение куба плоскостью MKP методом следа
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Презентация «Метод следов»
Описание метода следов для построения сечений
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Геометрия, 10 класс Тема : Построение сечений многогранников методом «следа». Воробьев Леонид Альбертович, г.Минск
Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть точки данного многогранника. Сечением многогранника называется фигура, состоящая из всех точек, которые являются общими для многогранника и секущей плоскости. Основные понятия Рис.1 Рис.2
Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон этого многоугольника не может превышать количества граней данного многогранника. Например (см.рис.3), в пятиугольной призме (всего 7 граней) в сечении могут получиться: треугольник, 4-угольник, 5-угольник, 6-угольник или 7-угольник. Рис.3
Две плоскости пересекаются по прямой (эта аксиома и дала названию метода – под «следом» понимается прямая пересечения какой-либо грани многогранника и секущей плоскости). Получение «следа» сводится к получению двух точек, принадлежащих одновременно какой-нибудь грани многогранника и секущей плоскости (подумайте, почему именно двух!?). Точки получаются как пересечение двух прямых, принадлежащих одной и той же плоскости . ПРИМЕЧАНИЕ . Не забудьте, что прямая и плоскость являются бесконечными в пространстве фигурами! Проследим на примере построение сечения куба плоскостью, заданной тремя данными точками M , N и K.
A B C D B 1 C 1 D 1 M N K Выбираем точки М и N , принадлежащие одной грани и строим прямую MN – «след» пересечения правой грани и секущей плоскости. A 1 ПРИМЕР 1.
A B C D B 1 C 1 D 1 M N K A 1 E Теперь обращаем внимание, что ребро куба В 1 С 1 лежит в одной грани с третьей точкой сечения К (верхней) и в одной грани с появившейся прямой MN (правой). Находим точку пересечения этих прямых – точку Е. ПРИМЕР 1.
A B C D B 1 C 1 D 1 M N K A 1 E Точки Е и К принадлежат верхней грани и секущей плоскости. Значит, прямая ЕК – «след» их пересечения и F D 1 C 1 , EK. F ПРИМЕР 1.
A B C D B 1 C 1 D 1 M N K A 1 E F Далее видим, что ребро куба А 1 В 1 лежит в одной грани с появившимся следом ЕК (верхней). Находим точку пересечения этих прямых – точку G . G ПРИМЕР 1.
A B C D B 1 C 1 D 1 M N K A 1 E F G Полученная точка G лежит в одной грани с точкой М (в передней) и обе точки принадлежат секущей плоскости – значит, прямая GM – очередной «след»! Причем, GM ∩ АА 1 =Н. H ПРИМЕР 1.
A B C D C 1 D 1 M N K A 1 E F G H Остается соединить отрезками все пары точек, лежащие в секущей плоскости и в одной грани куба. Полученный пятиугольник MNFKH – искомое сечение куба. B 1 ПРИМЕР 1.
ПРИМЕР 2. M N K Построить сечение четырехугольной пирамиды, заданное точками M,N и K . Проследите за ходом построения сечения и запишите его.
ПРИМЕР 3. Построить сечение пятиугольной призмы, заданное точками M,N и K . Проследите за ходом построения сечения и запишите его. M N K
M N K Рассмотрим теперь более сложные примеры ПРИМЕР 4.
M N K Помним о том, что вершина пирамиды – общая точка для всех боковых граней! ПРИМЕР 5.
Плоскость сечения может задаваться: 1) тремя точками, не лежащими на одной прямой; 2) прямой и точкой, не лежащей на ней; 3) двумя пересекающимися прямыми; 4) двумя параллельными прямыми. Все эти случаи можно свести к первому, выбирая на прямых удобные для нас точки.
Заключение Данный метод построения сечений многогранников можно применять, если найдется хотя бы одна пара точек, лежащих в секущей плоскости и одной грани многогранника. После чего задача циклично алгоритмизируется в получение очередной точки и очередного «следа». ПРИМЕЧАНИЕ. Если такой пары точек не найдется, то сечение строится методом параллельных проекций. Но это уже тема нового урока!