Ось симметрии 4 порядка в кубе

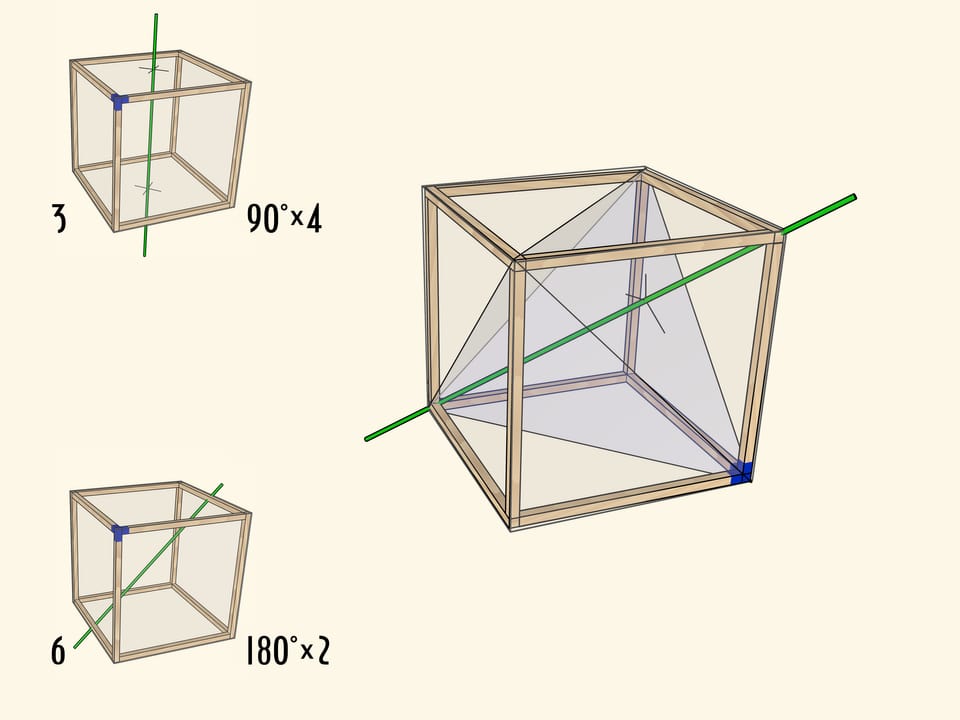
Оси вращения куба ⁠

Какие пово­роты пере­во­дят куб в себя, и сколько их? Какими осями опре­де­ляются эти пово­роты?

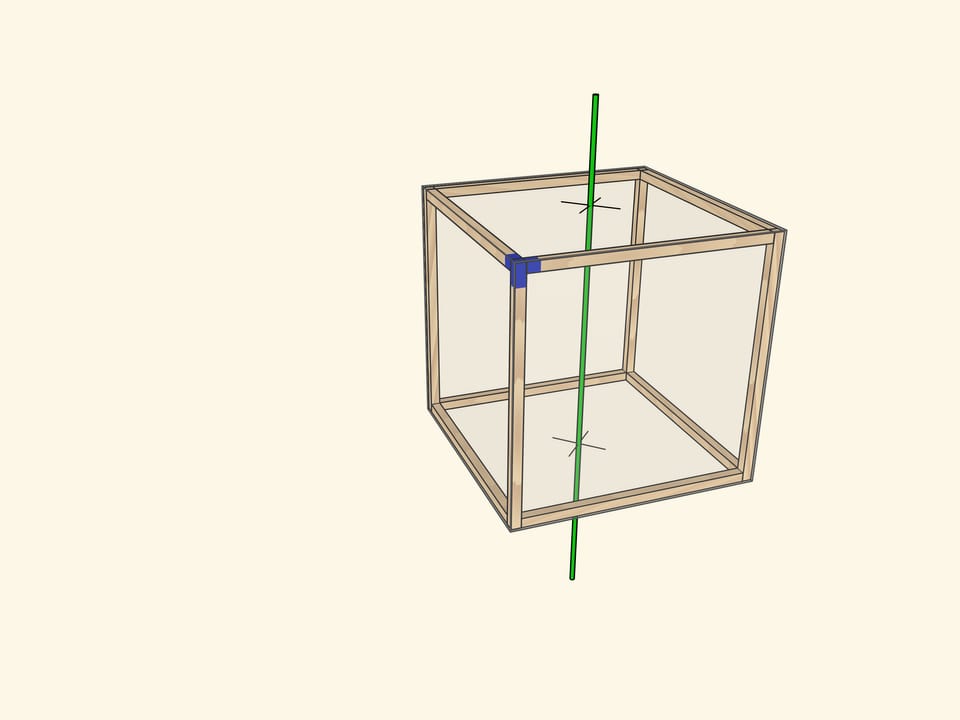
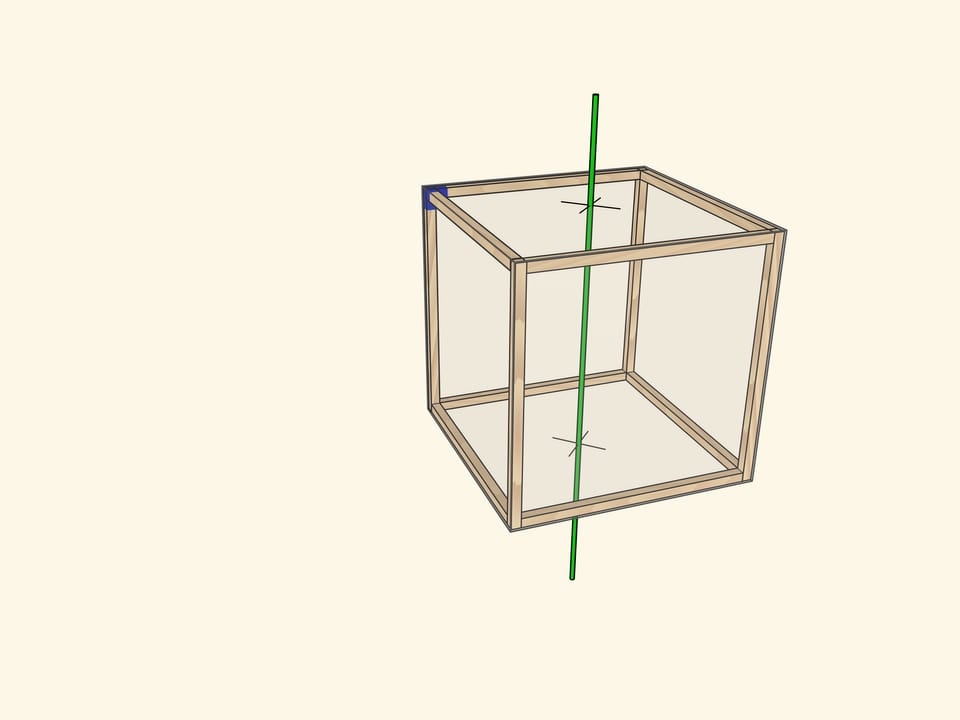
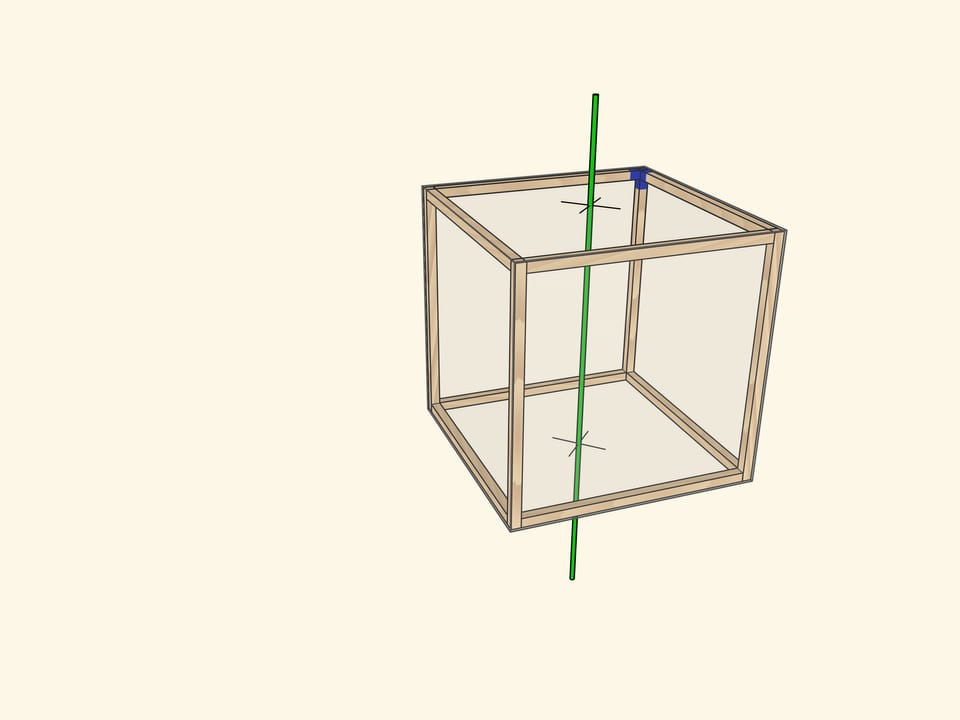
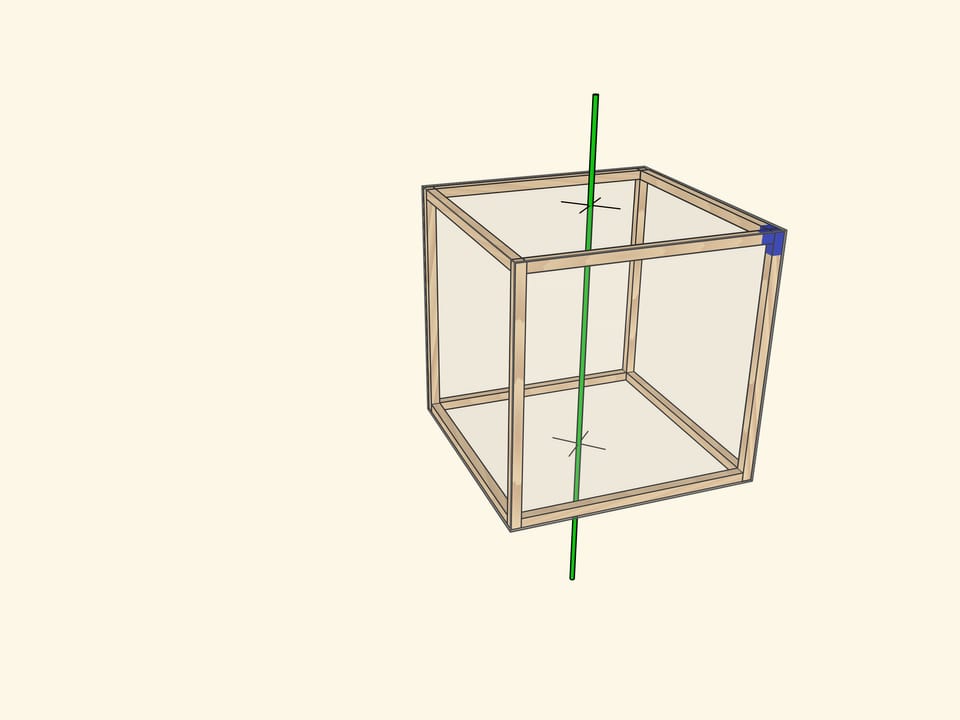
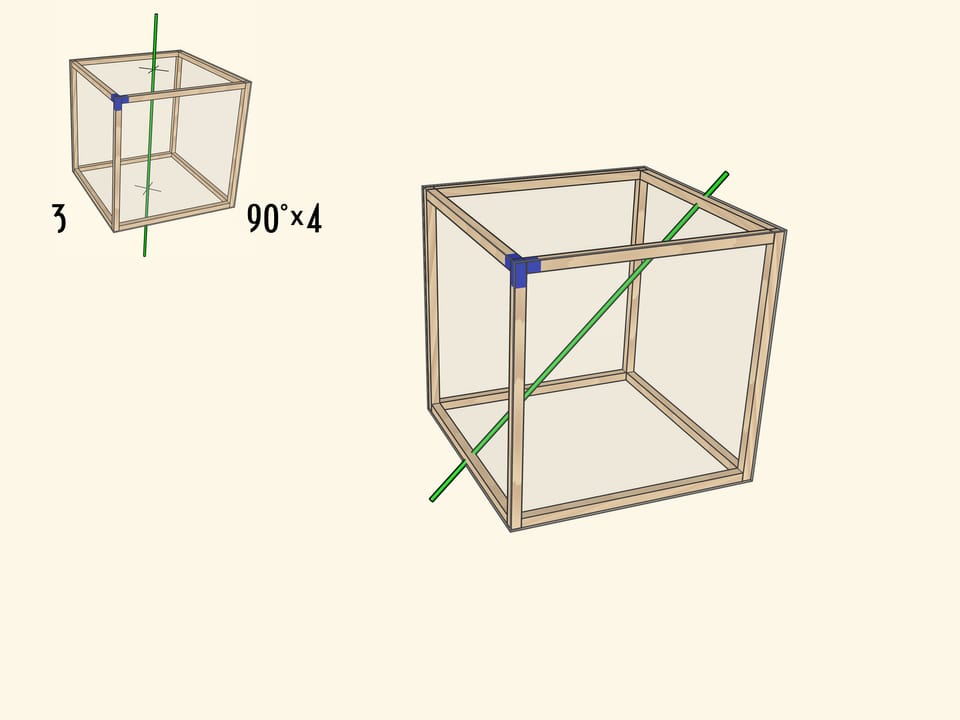
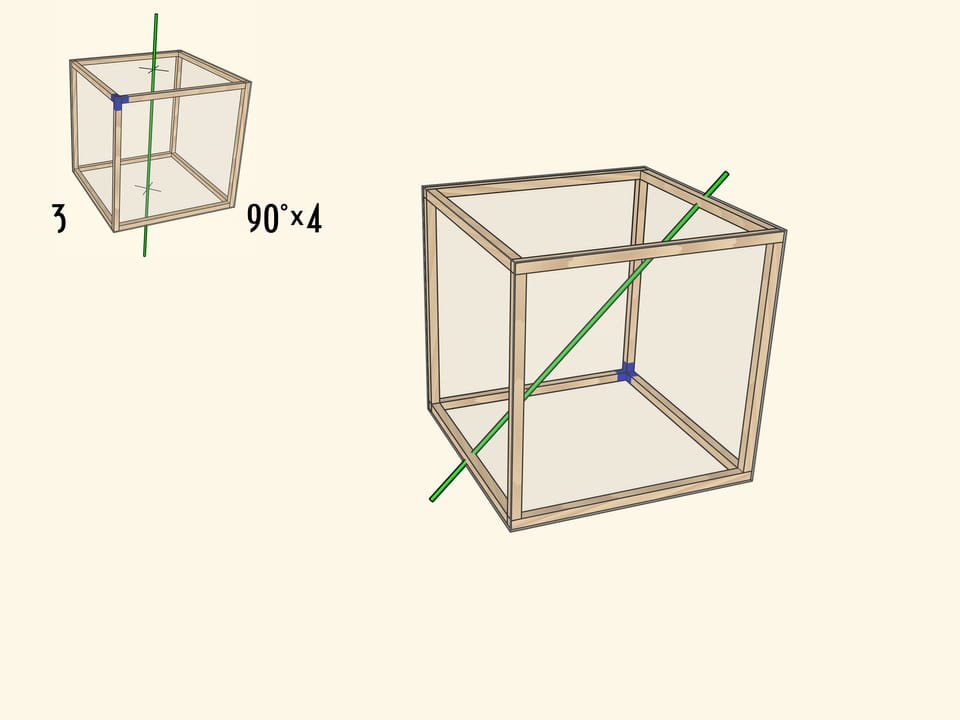
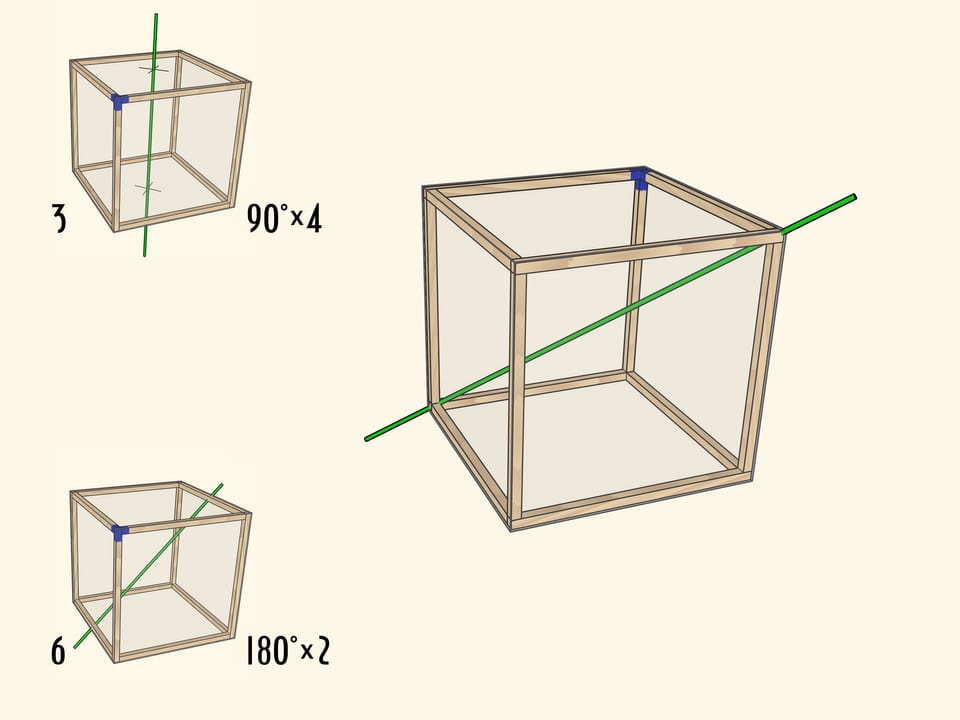
Самая оче­вид­ная ось про­хо­дит через цен­тры про­ти­вопо­лож­ных гра­ней куба. При пово­роте на $90^\circ$ куб пере­хо­дит в себя, а после четырёх таких пово­ро­тов ока­зы­ва­ется в исход­ном положе­нии. Осей чет­вёр­того порядка у куба $3$: столько же, сколько пар про­ти­вопо­лож­ных гра­ней.

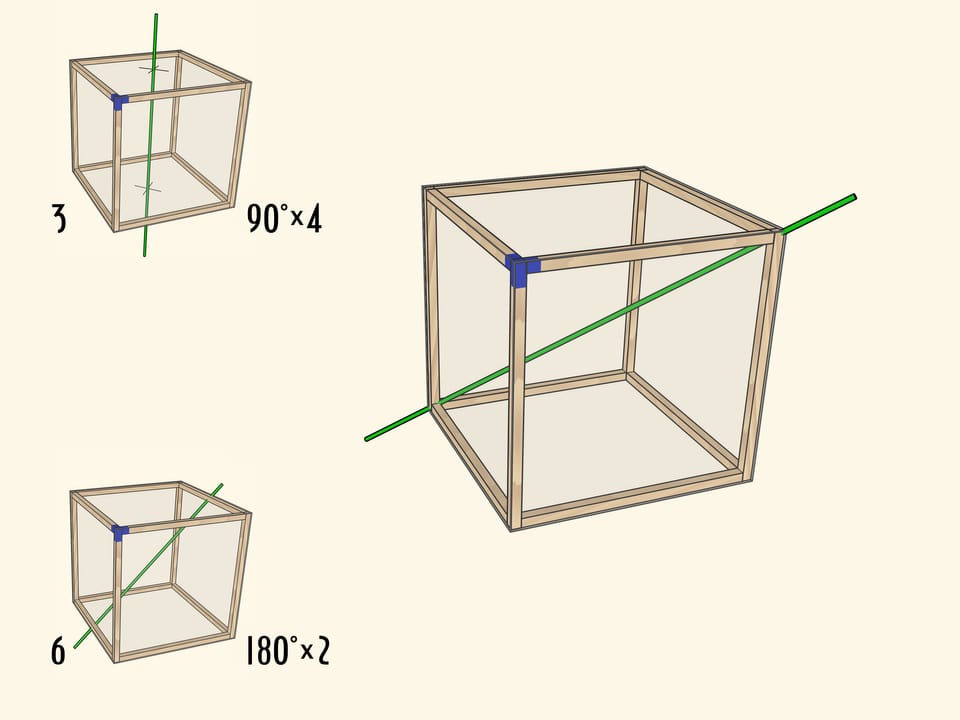
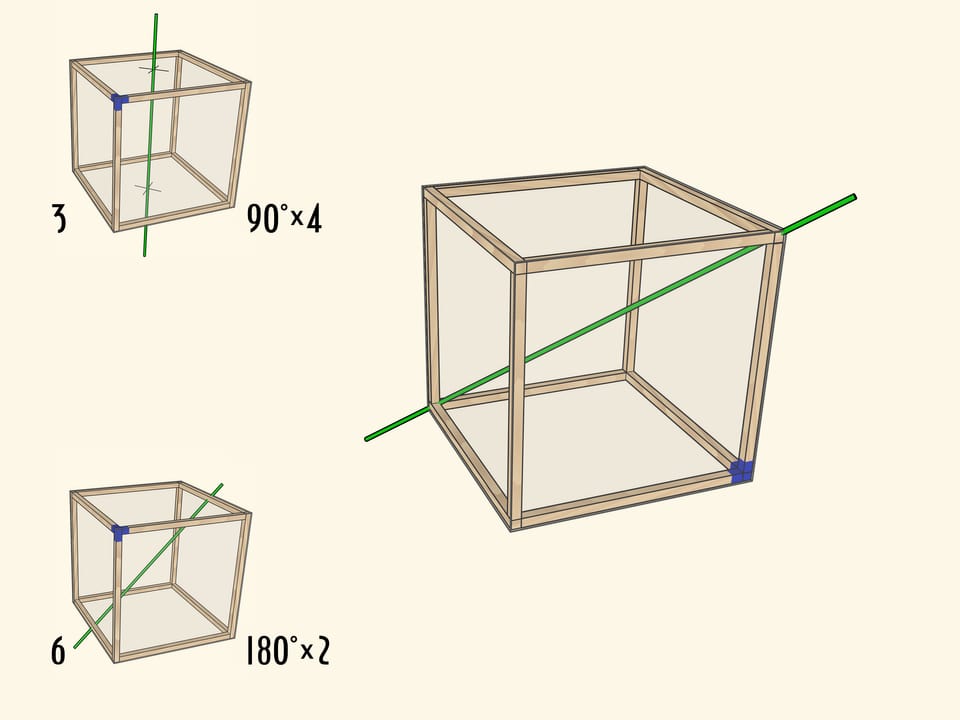
Менее оче­видно, что у куба есть ось вто­рого порядка — ось, про­хо­дящая через сере­дины про­ти­вопо­лож­ных рёбер куба. Таких осей всего $6$.

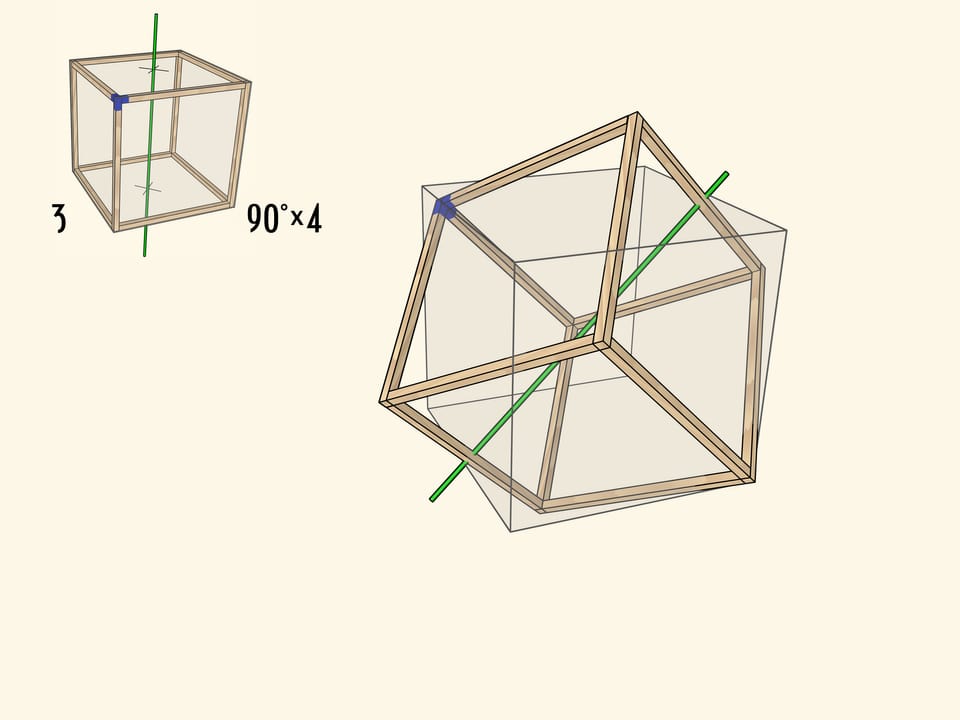
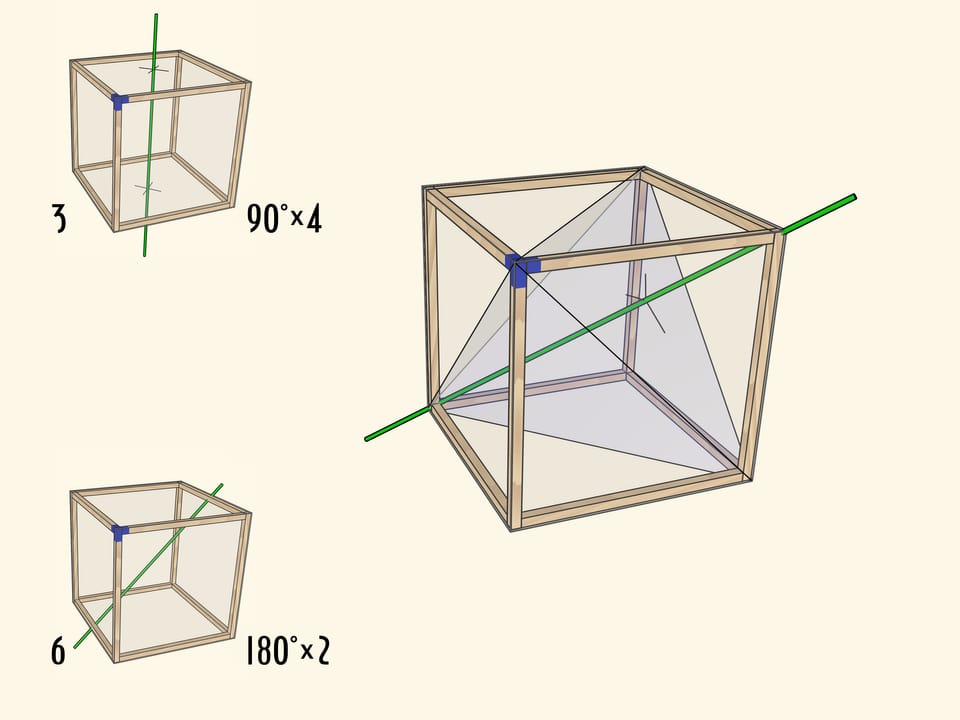
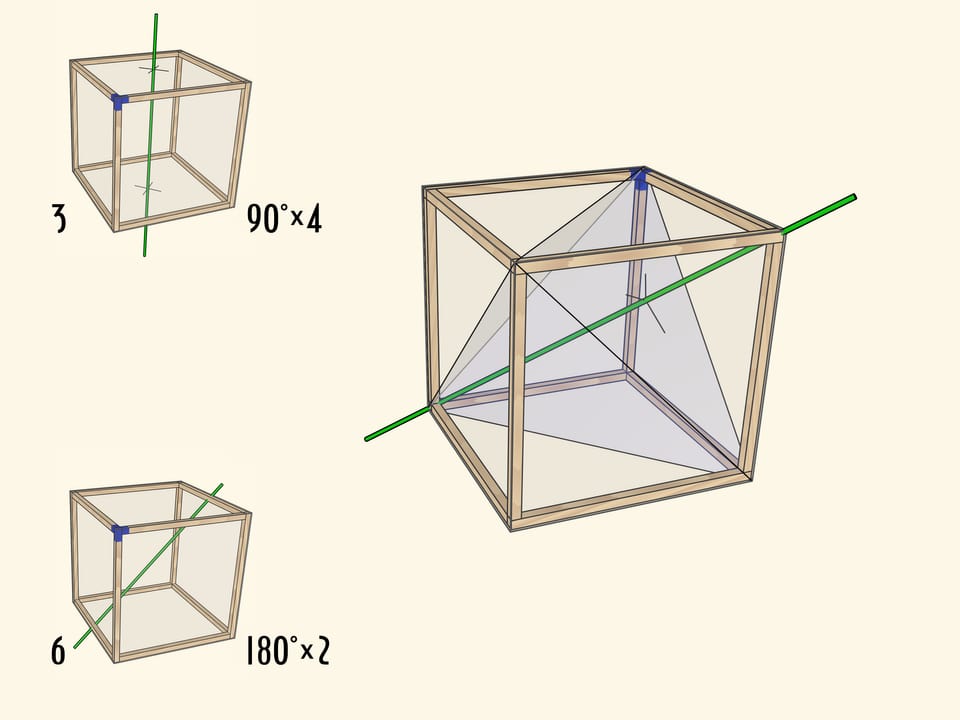
Ну и совсем уже неоче­видно на пер­вый взгляд, что у куба есть оси враще­ния тре­тьего порядка. Это диаго­нали куба.

Суще­ство­ва­ние таких осей ста­но­вится оче­вид­ным, если вспом­нить, что в куб ⁠ ⁠ можно ⁠ ⁠ впи­сать пра­виль­ный тет­раэдр.

Каж­дый тип пово­рота можно пред­ста­вить как отдель­ную модель с закреп­лён­ной в плос­ко­сти осью (под соот­вет­ствующим углом) и кубом, вращающимся на соот­вет­ствующие этой оси углы.

Пере­чис­лены все враще­ния, пере­во­дящие куб в себя, — других нет. А сово­куп­ность всех пово­ро­тов многогран­ника обра­зует группу: любые два после­до­ва­тельно сде­лан­ные пово­рота являются каким-то из уже пред­став­лен­ных пово­ро­тов. Попро­буйте понять, что будет компо­зицией двух пово­ро­тов отно­си­тельно каких-то несовпа­дающих осей, пово­ро­том вокруг какой оси и на какой угол. Коли­че­ство раз­лич­ных пово­ро­тов, пере­во­дящих куб в себя — поря­док группы — равно $24.$

Вме­сте с тож­де­ствен­ным это $3$ пово­рота на $90^\circ$ вокруг каж­дой из $3$ осей чет­вёр­того порядка (а чет­вёр­тый пово­рот — уже тож­де­ствен­ное пре­об­ра­зо­ва­ние), по $2$ пово­рота на $120^\circ$ вокруг $4$ осей тре­тьего порядка и пово­роты на $180^\circ$ вокруг $6$ осей вто­рого порядка: $1+3\cdot3+4\cdot 2+6\cdot1=24$. Заме­тим, что $24=4!$ — коли­че­ство пере­ста­но­вок четырёх пред­ме­тов, так как каж­дому пово­роту куба соот­вет­ствует пере­ста­новка на множе­стве его диаго­на­лей.

Источник

Ось симметрии 4 порядка в кубе

Симметрии куба, как и симметрии тетраэдра делятся на два типа — самосовмещения, при которых точки куба не изменяют своего положения относительно друг друга, и преобразования, оставляющие куб в целом на месте, но передвигающие его точки относительно друг друга. Преобразования первого типа мы, как и в случае тетраэдра, будем называть вращениями. Все вращения, очевидно, образуют группу, которая называется группой вращений куба. Опишем сначала строение этой группы.

Имеется ровно 24 вращения куба вокруг различных осей симметрии.

В самом деле, при поворотах куба место нижней грани может занять любая из 6 граней куба (рис. 28). Для каждой из 6 возможностей — когда указано, какая именно грань расположена внизу, — имеется 4 различных расположения куба, соответствующих его поворотам вокруг оси, проходящей через центры верхней и нижней граней, на углы

Таким образом, получаем вращений куба. Укажем их в явном биде.

Куб имеет центр симметрии (точка пересечения его диагоналей), 3 оси симметрии четвертого порядка, 4 оси симметрии третьего порядка и 6 осей симметрии второго порядка. Достаточно рассмотреть вращения вокруг осей симметрии.

а) Оси симметрии четвертого порядка — это оси проходящие через центры противоположных граней: Вокруг каждой из этих осей имеется по три нетождественных вращения, а именно вращения на углы . Этим вращениям соответствуют 9 перестановок вершин куба, при которых вершины противоположных граней переставляются циклически и согласовано. Например, перестановки

отвечают поворотам вокруг оси .

б) Осями симметрии третьего порядка являются диагонали куба. Вокруг каждой из четырех диагоналей [1, 7], [2, 8], [3, 5], [4, 6] имеется по два нетождественных вращения на углы . Например, вращения вокруг диагонали [1, 7] определяют такие перестановки вершин куба:

Всего получаем 8 таких вращений.

в) Осями симметрии второго порядка будут прямые, соединяющие середины противолежащих ребер куба. Имеется шесть пар противоположных ребер (например, [1, 2], [7, 8]), каждая пара определяет одну ось симметрии, т. е. получаем 6 осей симметрии второго порядка. Вокруг каждой из этих осей имеется одно нетождественное вращение. Всего — 6 вращений. Вместе с тождественным преобразованием получаем 9 + 8 + 6 + 1 = 24 различных вращения. Итак, все вращения куба указаны. Вращения куба определяют перестановки на множествах его вершин, ребер, граней и диагоналей.

Рассмотрим, как действует группа вращений куба на множестве его диагоналей. Различные вращения куба переставляют диагонали куба по-разному, т. е. им соответствуют различные перестановки на множестве диагоналей (проверьте!). Поэтому группа вращений куба определяет группу перестановок на множестве диагоналей, состоящую из 24 перестановок. Поскольку куб имеет лишь 4 диагонали, группа всех таких перестановок совпадает с симметрической группой на множестве диагоналей. Итак, любая перестановка диагоналей куба соответствует некоторому его вращению, причемразным перестановкам соответствуют разные вращения.

Опишем теперь всю группу симметрий куба. Куб имеет три плоскости симметрии, проходящие через его центр. Симметрии относительно этих плоскостей в сочетании со всеми вращениями куба дают нам еще 24 преобразования, являющихся самосовмещениями куба. Поэтому полная группа симметрий куба состоит из 48 преобразований.

Источник

Ось симметрии 4 порядка в кубе

Куб
Тип	Платоново твердое тело
Лица	6 квадратов
Края	12
Вершины	8
Грани / вершина	3
Характерная черта	2
Символ Шлефли
Символ Wythoff	3
Диаграмма Кокстера-Дынкина
Двойной	Правильный октаэдр
Группа симметрии	О ч
Объем	а³
Область	6a²
Двугранный угол	90 °
Характеристики	выпуклый зоноэдр
редактировать

В евклидовой геометрии , А куба является правой призма , чьи лица являются квадратными и , следовательно , равны и совмещаются. Куб — одно из самых замечательных тел в космосе . Это единственное из пяти тел Платона , имеющее ровно 6 граней, 12 ребер и 8 вершин. Другое его название — « правильный шестигранник ».

Поскольку у него четыре вершины на грань и три грани на вершину, его символ Шлефли равен <4.3>.

Этимология слова куб — греческое ; куб происходит от кубоса , игральной кости .

Термин куб , применяемый к числу , обозначает значение, полученное путем умножения этого числа на само себя и умножения результата на исходное число. Это выражение появилось в период, когда геометрическая алгебра была повсеместной, квадрат числа рассматривался как площадь квадрата помимо исходного числа, а куб числа — как объем куба помимо исходного числа. Выражение « 3 » может быть « излучающая в кубе» и «куб».

1-скелет кубы — множество его вершин , соединенных его ребра — образует графу называется шестигранный графом .

Резюме

Геометрия

Куб — одно из пяти тел Платона . Куб принадлежит к семейству прямых призм . У него 8 вершин и 12 ребер . В качестве вершин можно взять, например, точки координат . Более того : р 3 <\ Displaystyle \ mathbb ^ <3>> ( ± 1 , ± 1 , ± 1 ) <\ Displaystyle (\ pm 1, \ pm 1, \ pm 1)>

• Два ребра, имеющие общий конец, ортогональны.
• Противоположные грани параллельны . Соседние грани перпендикулярны
• Все двугранные углы являются прямыми .
• Эти диагонали пересекаются в одной точке, центр симметрии куба, в isobarycenter из восьми вершин.

Но по определению все его ребра имеют одинаковую длину, скажем a . Следовательно, его грани представляют собой квадраты с площадью а 2 .

• Таким образом, площадь куба составляет 6 к 2 ;
• его объем является равным 3 ;
• длина диагонали равна √ 3 ;
• описанная сфера , следовательно , к радиусу составляет √ 3 /2;
• касательная к краям сфера имеет радиус a / √ 2 ;
• вписанная сфера имеет радиус a / 2;
• угол между диагональю и каждой из смежных кромок равен arccos ⁡ ( 1 3 ) ≃ 54 , 74 ∘ . <\ displaystyle \ arccos \ left (<\ frac <1><\ sqrt <3>>> \ right) \ simeq 54 <,>74 ^ ​​<\ circ>.>
• угол между диагональю и каждой из смежных плоскостей равен арктан ⁡ ( 1 2 ) ≃ 35 год , 26 ∘ . <\ displaystyle \ arctan \ left (<\ frac <1><\ sqrt <2>>> \ right) \ simeq 35 <,>26 ^ <\ circ>.>

Именно выражение его объема привело к использованию слова « куб» в алгебре .

Другие определения

Есть и другие эквивалентные определения куба:

• кубы — единственные многогранники , у которых все грани квадратные;
• куб представляет собой антиалмаз порядка 3 с правильными вершинами и равными двугранными углами.

Группа изометрий

Группа изометрий куба, обозначенная O _h , и подгруппа его положительных изометрий (его поворотов ), обозначенная O, также называются октаэдрическими группами симметрии , потому что они такие же, как у его двойственного многогранника , l ‘ правильного октаэдра. .

Куб — один из самых симметричных многогранников:

• 3 оси вращения четвертого порядка: оси, проходящие через центр двух противоположных граней;
• 6 осей вращения 2-го порядка: оси, проходящие через середину двух противоположных граней;
• 4 оси вращения третьего порядка: оси, проходящие через две противоположные вершины;
• центральная симметрия относительно центра куба;
• 9 плоскостей симметрии : 3 плоскости, соединяющие края, 6 плоскостей, проходящие через два противоположных края.

Изометрия куба фиксирует его центр. Таким образом, он полностью определяется изображением вершины A и двух (B и C) из трех ее соседей (поскольку эти три точки вместе с центром образуют опорную точку в пространстве ). Вершина A может иметь в качестве образа любую A ‘из 8 вершин куба. Тогда для вершины B есть 3 возможных изображения среди трех соседей A ‘, затем для изображения C — 2 изображения среди двух оставшихся соседей. Это доказывает, что изометрии, оставляющие куб глобально инвариантным, равны 8 × 3 × 2 = 48, включая 24 поворота, и только одно из двух изображений C дает одинаковую ориентацию A’B’C ‘относительно ABC. 24 вращения:

• приложение идентичности, которое представляет собой вращение (на нулевой угол и любую ось);
• 3 осевых полуоборота, проходящие через центр двух противоположных граней (возможно 3 оси);
• 6 четверть оборота оси, проходящей через центр двух противоположных граней (3 возможных оси и 2 возможных угла);
• 6 полуоборотных осей, проходящих через середины двух противоположных краев (возможно 6 осей);
• 8 третей поворота оси проходит через две противоположные вершины (4 возможных оси и 2 возможных угла).

Группа О из этих 24 вращений является изоморфной к симметрической группой S ₄ . Любое вращение фактически переставляет четыре диагонали куба, и, наоборот, любая перестановка четырех диагоналей определяет одно вращение.

Отрицательные изометрии куба — это антиротации, составленные из этих вращений по центральной симметрии и коммутирующие с ней. Таким образом, группа O _h является прямым внутренним произведением подгруппы O на циклическую подгруппу порядка 2, порожденную центральной симметрией. Это самая большая из 7 ортогональных групп трехмерных сетей .

24 отрицательных изометрии соответственно:

• центральная симметрия
• 3 симметрии относительно плоскости, проходящей через центр куба и параллельной грани (3 возможных плоскости);
• 6, состоящий из предшествующих симметрий с четвертью оборота оси, перпендикулярной плоскости симметрии (3 возможных плоскости и 2 возможных угла);
• 6 симметрий относительно плоскости, проходящей через два противоположных края (6 возможных плоскостей);
• 8, состоящий из шестой части поворота оси, проходящей через две противоположные вершины с симметрией относительно плоскости, проходящей через центр куба и перпендикулярной этой оси (4 возможных оси и 2 возможных угла). Плоскость симметрии пересекает ребра куба, образуя правильный шестиугольник.

Наконец, восемь вершин куба можно разделить на два правильных тетраэдра , симметричных друг другу по центральной симметрии. Отсюда следует, что из 48 изометрий куба 24 оставляют каждый из этих тетраэдров инвариантным, а 24 меняют два тетраэдра. 24 изометрии куба, оставляющие тетраэдры инвариантными, образуют группу изометрий тетраэдра: 12 — вращения, а 12 — косвенные изометрии. Эти 24 изометрии переставляют четыре вершины тетраэдра.

Узоры

Есть одиннадцать шаблонов куба; вот четыре:

Развитие кросс , боковые квадраты могут быть размещены ниже или выше

Источник