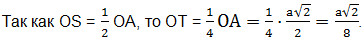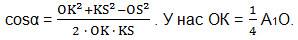Объем куба равен 70 построены сечение проходящей через середины ребер

Содержание

Объем куба равен 70 построены сечение проходящей через середины ребер
Объем куба равен 70 построены сечение проходящей через середины ребер
ЕГЭ ФИПИ-2015, задача 16 (варианты 14, 15)
14. Стереометрия

Объем куба равен 70 построены сечение проходящей через середины ребер

Объем куба равен 52. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

Поскольку высота куба равна высоте призмы, их объемы пропорциональны площадям их оснований. Площадь основания построенной призмы в 8 раз меньше площади основания исходной, поэтому искомый объем призмы равен 52 : 8 = 6,5.

Объём куба ABCDA₁B₁C₁D₁ равен 70. Построено сечение EFF₁1E₁, проходящее через середины рёбер BC, CD и C₁D₁ и параллельное ребру CC₁. Найдите объём треугольной призмы CEFC₁E₁F₁.

Объём куба равен 24. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

Объем куба равен 94. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

Это задание ещё не решено, приводим решение прототипа.

Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

Источник

Объем куба равен 70 построены сечение проходящей через середины ребер

Это задание ещё не решено, приводим решение прототипа.

Источник

ЕГЭ ФИПИ-2015, задача 16 (варианты 14, 15)

Две параллельные плоскости, находящиеся на расстоянии 8 друг от друга, пересекают шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 9π.

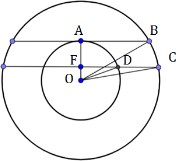
б) Найдите площадь поверхности шара.

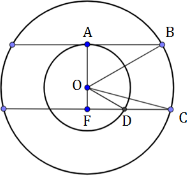
Решение. Всякое сечение шара плоскостью есть круг.

Каждая из плоскостей удалена от центра шара на 4, представляет собой круг, радиус которого равен 3.

Тогда радиус шара ОА=5 (египетский треугольник имеет стороны 3; 4; 5). Площадь поверхности шара S=4πR 2 ; S=4π·5 2 =100π (кв. ед.).

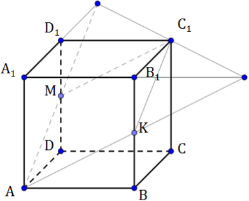
а) Постройте сечение куба плоскостью, проходящей через середины его рёбер АВ, В₁С₁, АD.

б) Найдите угол между плоскостью A₁BD и плоскостью, проходящей через середины рёбер АВ, В₁С₁, АD.

Середина АВ – точка М; середина В₁С₁ – точка N, середина AD – точка P. Проведем прямую МР – пересечения плоскости MNP с основанием. Секущая плоскость MNP пересечет верхнее основание по прямой, проходящей через точку N параллельно МР, и эта прямая NE пересечет C₁D₁ в точке Е — середине C₁D₁. Прямая МР пересечет CD в точке Х. Таким образом, секущая плоскость имеет с гранью CC₁D₁D две общие точки Е и Х, поэтому пересечет эту грань по прямой EF, причем точка F – середина DD₁. Прямая МР пересечет ВС в точке У. Тогда плоскость MNP пересечет грань ВВ₁С₁С по прямой УN и пересечет ВВ₁ в точке Z, которая также является серединой ВВ₁. Переднюю грань куба плоскость MNP пересечет по прямой ZМ. Итак, мы построили сечение куба плоскостью, проходящей через середины его рёбер АВ, В₁С₁, АD. Получился правильный шестиугольник MZNEFP.

Плоскость A₁BD – правильный треугольник, стороны которого являются диагоналями равных квадратов – граней куба. Плоскости MNP и A₁BD имеют две общие точки Q и Q₁, следовательно, пересекутся по прямой QQ_1.

Найдем угол между плоскостью A₁BD и плоскостью MNP. Это будет угол, образованный двумя полупрямыми, перпендикулярными QQ₁ – линии пересечения наших плоскостей. Построим этот угол.

Проведем A₁О, где О – пересечение диагоналей квадрата ABCD. Медиана A₁О в равностороннем ∆BA₁D является и высотой. A₁О пересечет в точке К отрезок QQ₁, который делит стороны A₁B и A₁D в отношении 1 : 4, считая от точек В и D, следовательно, и ОК : A₁О = 1 : 4.

Почему в отношении 1: 4? Смотрите:

Медиана BQ в этом треугольнике, проведенная к гипотенузе, равна половине гипотенузы, т.е.

Следовательно, BQ : A₁B = 1 : 4. Аналогично, DQ₁ : A₁D =1 : 4. Треугольники A₁QQ₁ и A₁BD подобны по двум пропорциональным сторонам и углу ВА₁D между этими сторонами. QQ₁ II BD, треугольники QA₁K и BA₁O также подобны по углам, образованным соответственно параллельными сторонами, поэтому и ОК : A₁О = 1 : 4.

Так как А₁О ⊥ BD и QQ₁ II BD, то А₁О ⊥ QQ₁, а значит и OK⊥QQ₁.

Так как BD || MP и BD || QQ₁, то MP || QQ_1.

Обозначим через S точку пересечения MP с АС — диагональю квадрата АBСD.

KS – расстояние от МР до QQ₁, т.е. KS ⊥QQ₁ и угол OKS – линейный угол между плоскостью A₁BD и плоскостью MNP. Обозначим угол OKS через α. Проведем KT⊥OS. Треугольник OKT подобен треугольнику OA₁A и OT:OA=OK:ОА₁=1:4.

Так как в ∆OKS высота КТ является и медианой, то ∆OKS – равнобедренный. КТ– биссектриса искомого угла α. Обозначим угол А₁ОА через φ. Из прямоугольного ∆OAA₁ найдем

Углы при основании OS равнобедренного треугольника OKS равны φ, следовательно, угол α = 180°-2φ. Тогда tgα = tg(180 0 -2φ) = -tg2φ.

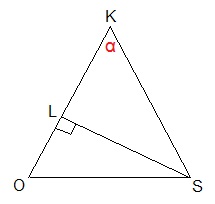
А можно решить так: установим, что ∆OKS – равнобедренный и проведем SL⊥OK.

Из прямоугольного треугольника SLK, по определению тангенса острого угла, следует, что tgα = SL : KL. Обозначим KL = x.

Из ∆KLS по теореме Пифагора: SL 2 =KS 2 -KL 2

Из ∆ОLS по теореме Пифагора: SL 2 =ОS 2 -ОL 2 . Левые части равенств равны, значит, и правые части равенств будут равны:

KS 2 -KL 2 = ОS 2 -ОL 2 . Подставляем данные:

Однако, на мой взгляд, самым целесообразным (естественным) было бы рассуждать так:

установили, что угол OKS – искомый и обозначили его через α. Применим теорему косинусов к этому треугольнику и выразим косинус α.

Высота А₁О в правильном треугольнике ВА₁D равна произведению стороны А₁В на синус 60° (катет, противолежащий углу, равен произведению гипотенузы на синус этого угла). Если ребро куба обозначить через а, то

где r₆ – радиус окружности, вписанной в правильный шестиугольник MZNEFP.

Если обозначить сторону правильного шестиугольника через b, то радиус вписанной окружности

Подставляем значения OK, KS, OS и найдем косинус α.

Дорогие друзья, мы решили данную задачу тремя способами (но понятно, что способов больше!), и вы должны знать, что вольны выбирать любой способ решения. Проверяющие вас экзаменаторы зачтут любое обоснованное решение. Да, ну а все же, давайте убедимся в том,

Источник

14. Стереометрия

Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.

Примеры ответов: 7 или здесьисейчас или 3514

Найдите площадь сечения, вершинами которого являются вершина А и середины рёбер ВВ₁ и DD₁единичного куба АВСDA₁B₁C₁D₁.

Дополнительное построение К – середина ребра ВВ₁ и М – середина ребра DD₁.

Строим сечение методом следов:

Соединяем вершины, лежащие в одной грани, А и К, А и М.
Продлеваем прямые АК и А₁В₁ до пересечения. Также прямые АМ и A₁D₁.
Соединяем точки и видим, что прямая, проходит через точку С₁, которая принадлежит нашему сечению.
Соединяем оставшиеся точки.

Сечением является ромб. Найдем его сторону по теореме Пифагора:

Большая диагональ куба является диагональю куба – АС₁.

Найдем угол АКС₁ по теореме косинусов:

$AC_1^2=AK^2+KC_1^2-2\cdot AK\cdot KC_1\cdot\cos AKC_1 \\[5pt] 3=\displaystyle\frac<5><4>+\frac<5><4>-2\cdot\frac<5><4>\cdot\cos AKC_1 \\[2pt] \cos AKC_1=-\displaystyle\frac<1><5>$

Найдем площадь искомого сечения:

Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5. Найдите площадь сечения большего шара плоскостью α.

Сечение шара плоскостью – круг.

Дополнительное построение – плоскость α имеет радиус АВ, плоскость β – FD и FC.

Площадь сечения большего шара плоскостью, параллельной первоначальной плоскости, равна 5. Значит: $S=\pi R^2=\pi\cdot AB^2=5$

Аналогичным образом найдем $FD^2=\displaystyle\frac<7><\pi>$

Для того, чтобы найти площадь искомого сечения, надо знать, чему равно CF 2 .

Применим теорему Пифагора:

Вычтем из одного уравнения другое.

Применим еще раз теорему Пифагора:

$OA^2+AB^2-OD^2=FC^2-FD^2 \\[3pt] OD=OA\rightarrow AB^2=FC^2-FD^2 \\ FC^2=AB^2+FD^2=\displaystyle\frac<5><\pi>+\frac<7><\pi>=\frac<12><\pi>$

Также возможен случай, когда плоскости будут по одну сторону от центра. Решение будет аналогичным.

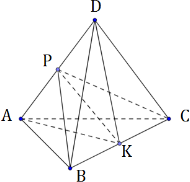
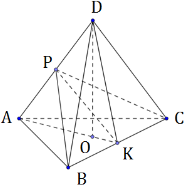
В треугольной пирамиде ABCD двугранные углы при рёбрах AD и BC равны. AB = BD = CD = AC = 5.

б) Найдите объем пирамиды, если двугранные углы при AD и BC равны 60.

1) Дополнительное построение:

2) Треугольники АВС и АBD равнобедренные по условию, значит, АК и BP будут являться медианами по свойству равнобедренного треугольника. Тогда DK, СР также являются одновременно медианой и высотой.

Тогда ∠BPC – линейный угол двугранного угла при ребре AD, ∠AKD — линейный угол двугранного угла при ребре ВС. Из условия имеем: ∠BPC = ∠AKD.

3) РК медиана, биссектриса и высота в треугольниках ВРС и AKD. Тогда PK ⊥ BC и PK ⊥ AD.

Тогда, треугольник BPK равен треугольнику АКР по углу

$\angle BPK=\displaystyle\frac<1><2>\angle BPC=\frac<1><2>\angle AKD=\angle AKP$ и катету РК.

Из равенства треугольников следует, что BK = AP.

$BK=\displaystyle\frac<1><2>BC \\[3pt] AP=\displaystyle\frac<1><2>AD$

1) По данным пункта б: ∠BPC = ∠AKD = 60°, тогда треугольники АКD и ВРС равносторонние. Пусть сторона каждого такого треугольника будет равна х.

2) Дополнительное построение. Пусть DO⊥ AK.

$\left\<\beginBC\perp KD\ (&по\ доказанному\ в\ пункте\ а) \\ BC\perp AK\ (&по\ доказанному\ в\ пункте\ а) \\ &KD\cap AK=K\end\right.\!\!\!\Rightarrow BC\perp AKD\ <(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)>$

Из доказанного следует, что BC ⊥ OD. Значит:

То есть, OD – высота пирамиды.

3) AK = x по построению, тогда $BK=\displaystyle\frac<2>.\ AB=5$.

Треугольник АВК прямоугольный, значит:

4) Высота пирамиды и равностороннего треугольника равна:

5) Площадь основания равна:

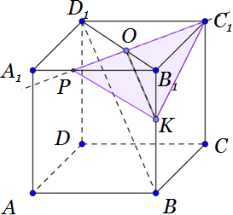
$S_=\displaystyle\frac<1><2>AK\cdot BC=\frac<1><2>\cdot x\cdot x=\frac<1><2>\cdot 2\sqrt<5>\cdot 2\sqrt<5>=10 \\ V=\displaystyle\frac<1><3>\cdot h\cdot S_=\frac<1><3>\cdot\sqrt<15>\cdot 10=\frac<10\sqrt<15>><3>$

В кубе $ABCDA_1B_1C_1D_1$ все рёбра равны 5. На его ребре BB₁ отмечена
точка K так, что KB = 3. Через точки K и С₁ проведена плоскость α, параллельная прямой BD₁.

а) Докажите, что $\displaystyle\frac=\frac<1><2>$, где P — точка пересечения плоскости α с ребром A₁B₁.

б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

а) 1. Дополнительное построение.

Пусть B₁D₁ пересекается с построенной прямой в точке О.

Прямая BD₁параллельная плоскости С₁ОК, так как параллельна как минимум одной прямой ОК (по построению), лежащей в этой плоскости.

2) Через точку С₁ и О проведем прямую. Пусть прямая С₁О пересекается с A₁B₁в точке Р. Точка Р – точка пересечения плоскости α с ребром A₁B₁.

3) В треугольнике BB₁D отрезок ОК параллелен BD₁. Значит отрезок ОК делит треугольник BB₁D на 2 подобных (признак подобия по 2 углам).

Что и требовалось доказать.

Ребро РВ₁ перпендикулярно В₁С₁К, так как $ABCDA_1B_1C_1D_1$ — куб, а значит является высотой пирамиды.

Найдем объем другой части куба.

Из объема всего куба вычтем объем пирамиды.

Источник