Куб разности формула как решать

Как использовать куб разности

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки.

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения.

Прежде чем перейти к этому уроку обязательно выучите наизусть все формулы сокращенного умножения.

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку.

Вспомним, как выглядит формула куба разности.

(a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Формула куб разности не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

a 3 − 3a 2 b + 3ab 2 − b 3 = (a − b) 3

Как возвести в куб разность

Рассмотрим пример. Необходимо возвести в куб многочлен, который содержит разность.

Используем формулу куба разности. Только вместо « a » у нас будет « 2y », а вместо « b » будет « x ».

Часто возводят многочлен в куб следующим образом:

Это неверно! Для возведения многочлена в куб необходимо использовать формулу сокращенного умножения: (a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Применение куба разности для разложения многочлена на множители

Рассмотрим многочлен. Требуется разложить его на множители, используя формулу куба разности.

Обратите внимание, что многочлен « x 3 − 3x 2 y + 3xy 2 − y 3 » напоминает правую часть формулы « a 3 − 3a 2 b + 3ab 2 − b 3 », только вместо « a » стоит « x », а на месте « b » стоит « y ».

Используем для многочлена « x 3 − 3x 2 y + 3xy 2 − y 3 » формулу куба разности.

Рассмотрим пример сложнее. Требуется разложить многочлен на множители.

В этом многочлене не так очевидно, что будет являться в формуле « a », а что « b ».

Представим многочлен « 8y 3 − 36y 2 + 54y − 27 » в виде « a 3 − 3a 2 b + 3ab 2 − b 3 ».

Обратим внимание, что « 8y 3 » — это « (2y) 3 », значит « a » в исходном многочлене — это « 2y ».

Чтобы понять, что является « b » в исходном многочлене, рассмотрим последний одночлен — « 27 ». Вспомним, что « 27 » — это « 3 3 », значит « b » в исходном многочлене — это « 3 ».

Рассмотрим одночлены посередине « 36y 2 » и « 54y ». При сравнении многочлена с кубом разности « a 3 − 3a 2 b + 3ab 2 − b 3 » можно понять, что эти одночлены должны быть « 3a 2 b » и « 3ab 2 соответсвенно.

Преобразуем одночлены « 36y 2 » и « 54y » в виде « 3a 2 b » и « 3ab 2 ». С учетом того, что ранее мы нашли, что в нашем многочлене « a » — это « 2y », а « b » — это « 3 ».

Внимательно проверяйте, правильно ли вы разложили числовые коэффициенты.

Проверим, верно ли мы разложили одночлены « 36y 2 » и « 54y ».

• 36y 2 = 3 · (2y) 2 · 3 = 3 · 4y 2 · 3 = 12y 2 · 3 = 36y 2 (верно)
• 54y = 3 · 2y · (3) 2 = 3 · 2y · 9 = 6y · 9 = 54y (верно)

После необходимых преобразований становится видно, что многочлен
« 8y 3 − 36y 2 + 54y − 27 » является правой частью формулы куба разности
« (a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3 ».

Используем формулу куба разности и решим пример до конца.

Источник

Куб суммы и разности двух выражений

Формула куба суммы

$$ = a(a^2+2ab+b^2 )+b(a^2+2ab+b^2 ) = a^3+2a^2 b+ab^2+a^2 b+2ab^2+b^3 = $$

Мы получили формулу куба суммы двух выражений:

Куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения на второе выражение, плюс утроенное произведение первого выражения на квадрат второго выражения, плюс куб второго выражения.

Вместо a и b в формуле могут быть любые одночлены (и даже многочлены), которые нужно подставить. Например:

Формула куба разности

Возведем в куб разность (a-b):

$$ = a(a^2-2ab+b^2 )-b(a^2-2ab+b^2 ) = a^3-2a^2 b+ab^2-a^2 b+2ab^2-b^3 = $$

Мы получили формулу куба разности двух выражений:

Куб разности двух выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе выражение, плюс утроенное произведение первого выражения на квадрат второго выражения, минус куб второго выражения.

Вместо a и b в формуле могут быть любые одночлены (и даже многочлены), которые нужно подставить. Например:

Не забывайте о втором и третьем слагаемом в формулах куба двучленов!

Не путайте знаки «+» и «-» перед слагаемыми!

Примеры

Пример 1. Представьте в виде многочлена

а) $ (x+5)^3 = x^3+3\cdot x^2\cdot5+3\cdot x\cdot5^2+5^3 = x^3+15x^2+75x+125$

б) $ (9-z)^3 = 9^3-3\cdot9^2\cdot z+3\cdot9\cdot z^2-z^3 = 729-243+27z^2-z^3 $

в) $(5b-3c)^3 = (5b)^3-3\cdot(5b)^2\cdot3c+3\cdot5b\cdot(3c)^2-(3c)^3 =$

г) $(2mk+1)^3 = (2mk)^3+3\cdot(2mk)^2\cdot1+3\cdot2mk\cdot1^2+1^3 =$

Пример 2. Упростите выражение:

а) $(a+2)^3-(a-2)^3 = a^3+3a^2\cdot2+3a\cdot2^2+2^3-(a^3-3a^2\cdot2+3a\cdot2^2-2^3 )= $

б) $(x-3y)^3+9xy(x-3y) = x^3-3x^2\cdot3y+3x\cdot(3y)^2-27y^3+9x^2 y-27xy^2 =$

в) $(x+y)^3-x(x-y)^2 = x^3-3x^2 y+3xy^2+y^3-x(x^2-2xy+y^2 ) =$

$= x^3-3x^2 y+3xy^2+y^3-x^3+2x^2 y-xy^2 = -x^2 y+2xy^2+y^3$

$-(k^3+3k^2\cdot3m+3k\cdot(3m)^2+(3m)^3 ) = 3k^2 m+18km^2+27m^3- $

$-k^3-9k^2 m-27km^2-27m^3 = -6k^2 m-9km^2-k^3 $

Пример 3. Найдите значение выражения:

a) $a^3-b^3-3ab(a-b)$ при a = -7 и b = -17

$a^3-b^3-3ab(a-b) = a^3-b^3-3a^2 b+3ab^2 = a^3-3a^2 b+3ab^2-b^3 =$

Подставляем: $(-7-(-17) )^3 = 10^3 = 1000$

б) $3ab(a+b)+a^3+b^3$ при a = -3 и b = 13

$ 3ab(a+b)+a^3+b^3 = 3a^2 b+3ab^2+a^3+b^3 = a^3+3a^2 b+3ab^2+b^3 = $

Подставляем: $(-3+13)^3 = 10^3 = 1000$

Пример 4. Решите уравнение:

$1-3\cdot4x+3\cdot(4x)^2-(4x)^3+48\cdot \frac<4> <3>x^3-48x^2 = 0 $

Пример 5*. Дайте геометрическое объяснение формуле куба суммы (аналогично квадрату суммы – см. §21 данного справочника, но для кубов в пространстве).

Рассмотрим куб со стороной (a+b) и вписанный в один из его углов куб со стороной b.

Объемы кубов $V_ = (a+b)^3,V_b = b^3$ Объем прямоугольного параллелепипеда, закрашенного оранжевым цветом: $V_ <ор>= a(a+b)^2$

Объем прямоугольного параллелепипеда, закрашенного синим: $V_ <син>= b(a+b)^2$

Источник

Формулы куба суммы и куба разности

Куб разности и суммы чисел

Вычисление куба суммы и разности чисел необходимы во всех разделах математики. Они применяются при решении многих неравенств и уравнений, упрощении выражений, разложении многочленов, вычислении пределов, сокращении дробей, решении интегралов.

Поэтому необходимо уметь их выводить, понимать смысл и уметь применять на практике.

Правило для куба суммы

Возведем в куб сумму чисел a и b. Для этого распишем выражение в виде многочлена:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Воспользуемся формулой квадрата суммы и получим следующее выражение:

Теперь умножаем многочлен на многочлен и получаем:

Упростим получившиеся выражение и получим формулу куба суммы:

Куб суммы двух выражений равен сумме куба первого, утроенного произведения квадрата первого на второе, утроенного произведения первого на квадрат второго и куб третьего.

Правило для куба разности

При любых значениях b и c верно равенство:

Докажем его. Для этого разложим куб разности двух чисел на множители:

Теперь умножим многочлен на многочлен и упростим выражение:

Таким образом, выведенное тождество верно для любых значений переменных b, c и называется формулой куба разности \(\left(b-c\right)^3=b^3-3b^2c+3bc^2-c^3\)

Она читается так: куб разности двух выражений равен кубу первого, минус утроенное произведение квадрата первого на второе, плюс утроенное произведение первого на квадрат второго, минус куб второго.

Куб разности трех чисел

Нередко при решении различных задач возникает необходимость вычислить куб разности трех чисел. Чтобы облегчить мыслительную работу можно вывести формулу и для этого случая:

Сложив подобные слагаемые придадим полученной формуле более удобный вид:

Она называется правилом куба разности трехчлена.

Аналогично можно вывести и формулу куба суммы трехчлена:

Примеры задач куба разности и суммы

Раскрыть скобки \(\left(2x-3y^2\right)^3\)

Если внимательно посмотреть на эту дробь, то можно увидеть, что в знаменателе представлен квадрат разности, а в числителе – куб разности.

Источник

Сокращенное умножение: правила, формулы

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

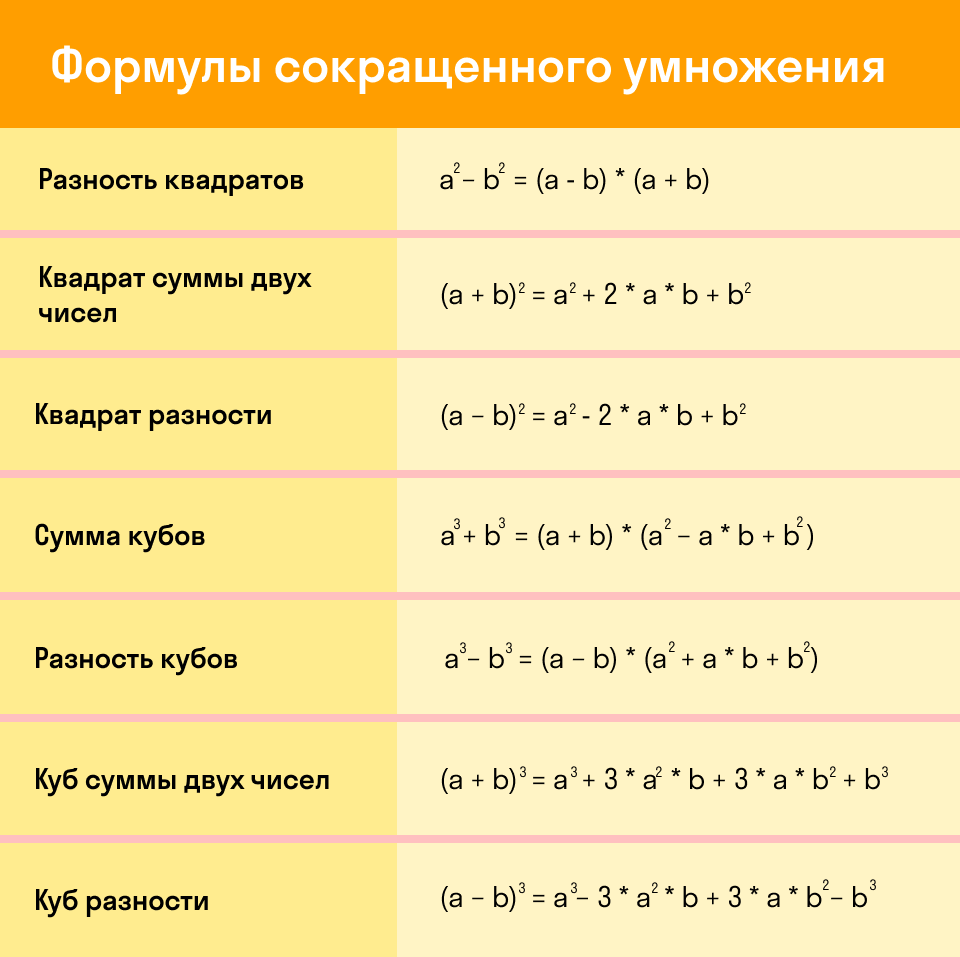
Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

1. Разность квадратов двух выражений равна произведению их разности и их суммы.
2. Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
3. Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
4. Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
5. Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
6. Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
7. Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a 2 — b 2 = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a 2 — b 2 .

Важно знать, что разность квадратов не равна квадрату разности: a 2 — b 2 ≠ (a — b) 2 .

Докажем, что a 2 — b 2 = (a — b) * (a + b).

Используя искусственный метод, прибавим и отнимем одно и тоже a * b.

a 2 — b 2 = a 2 — b 2 + ab — ab

1. Сгруппируем иначе: a 2 — b 2 + a * b — a * b = a 2 — a * b + a * b — b 2
2. Продолжим группировать: a 2 — a * b — b 2 +a * b = (a 2 — a * b) + (a * b — b 2 )
3. Вынесем общие множители за скобки:

   (a 2 — a * b) + (a * b — b 2 ) = a *(a — b) + b *(a — b)

1. Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
2. Результат доказательства: a 2 — b 2 = (a — b) * (a + b)
3. Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a 2 — b 2 , нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a 2 — b 2 .

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).

Для четных показателей можно записать так:

a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).

Для нечетных показателей:

a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10) 2 .

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с 3 – 8.

Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).

1. Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y 2 + 7 * y * x — 7 * y * x — x 2 = 49 * y 2 — x 2 .
2. Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y) 2 — x 2 = 49 * y 2 — x 2 .

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

Источник