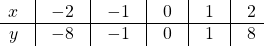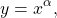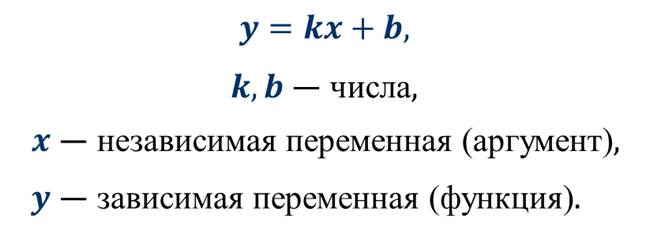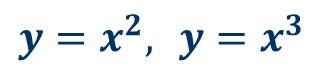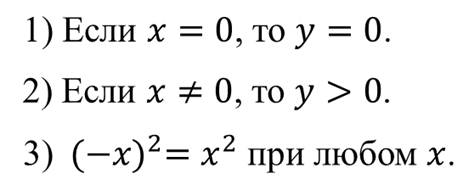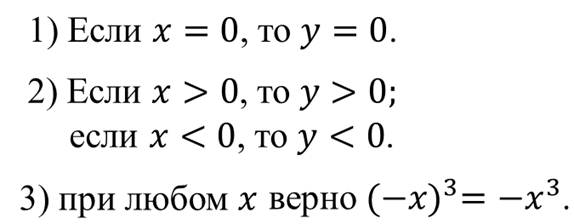Игрек равно икс в кубе что это за функция

Кубическая функция

Кубическая функция — это функция вида y=ax³, где a — число ( a≠0).

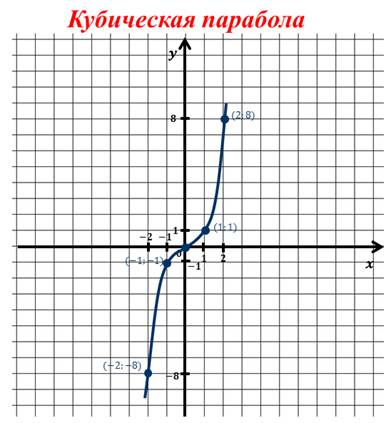
График кубической функции называется кубической параболой.

Для начала рассмотрим свойства и график кубической функции y=x³ (при a=1).

Свойства функция y=x³:

1) Область определения — множество действительных чисел:

2) Область значений — все действительные числа:

3) Функция имеет один нуль:

4) Точка O (0;0) делит кубическую параболу на две равные части, каждая из которых называется ветвью кубической параболы. Ветви кубической параболы симметричны относительно точки O — начала координат.

Отсюда следует, что противоположным значениям x соответствуют противоположные значения y: (- x)³= — x³ .

5) Функция возрастает на всей числовой прямой.

6) Промежутки знакопостоянства: функция принимает положительные значения при x∈(0;∞) (или y>0 при x>0);

функция принимает отрицательные значения при x∈(-∞;0) (или y

Эти точки отмечаем на координатной плоскости и строим кубическую параболу:

График функции y=ax³ при a≠1 ( a≠0) получают из графика функции y=x³ при помощи геометрических преобразований.

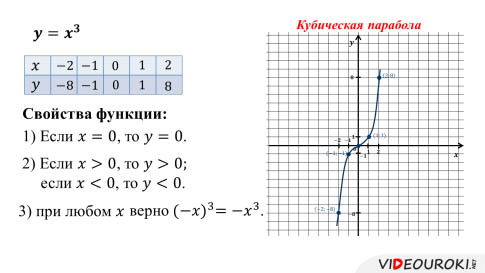
Функция y=x³ — один из частных случаев степенной функции

где α — любое действительное число.

В курсе алгебры из частных случаев степенной функции мы уже встречались с квадратичной функцией y=x² и функцией обратной пропорциональности

Источник

Функции y=x2 и y=x3 и их графики

Урок 23. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока «Функции y=x2 и y=x3 и их графики»

· рассмотреть функцию y = x 2 , её свойства и график;

· рассмотреть функцию y = х 3 , её свойства и график.

На одном из предыдущих уроков мы с вами познакомились с линейной функцией, которую можно задать формулой вида:

Также вспомним, что графиком линейной функции является прямая.

На этом уроке мы рассмотрим функции:

А точнее, мы научимся строить графики этих функций и выясним некоторые их свойства.

Начнём с того, что выразим формулой зависимость площади квадрата от длины его стороны.

Таким образом, зависимость площади квадрата от его стороны является примером функции.

Давайте построим график этой функции.

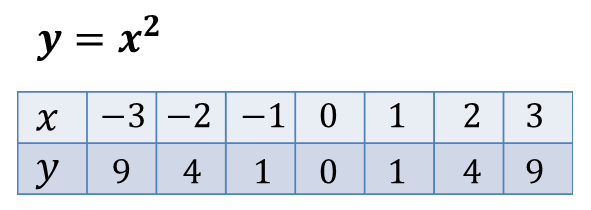
Составим таблицу значений x, y.

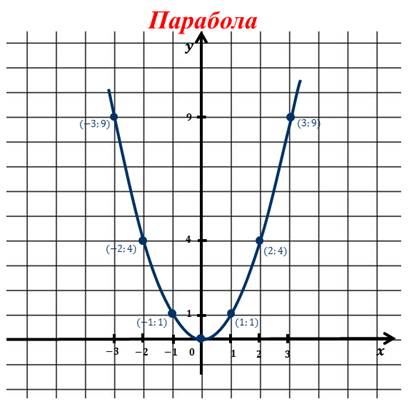
Далее полученные точки изобразим на координатной плоскости и проведём через них плавную линию.

Обратите внимание, что этот график неограниченно продолжается вверх справа и слева от оси игрек.

Теперь выясним некоторые свойства функции y = x 2 .

Из последнего свойства графика следует, что точки графика, имеющие противоположные абсциссы, симметричны относительно оси игрек.

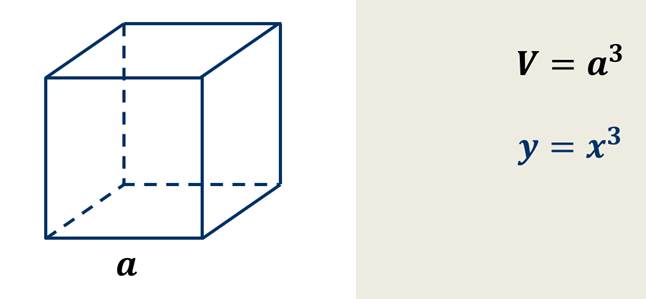
Теперь давайте выразим формулой зависимость объёма куба от длины его ребра.

Если мы будем менять длину ребра, то и его объём будет меняться.

Зависимость объёма куба от длины его ребра является примером функции.

Построим график этой функции. Для этого придадим несколько значений аргументу икс и вычислим соответствующие значения функции.

Изобразим точки с полученными координатами на координатной плоскости и проведём через них плавную линию.

Обратите внимание, что этот график можно неограниченно продолжать справа от оси игрек вверх и слева от оси игрек вниз.

Поговорим о свойствах функции игрек равняется икс в кубе.

Следовательно, точки графика, которые имеют противоположные абсциссы, расположены симметрично относительно начала координат.

В повседневной жизни представление о параболе дают нам, например, траектории прыжков животных, радуга. Тросы висячего моста напоминают нам параболы.

Также параболу часто можно встретить в архитектуре.

Источник

Построить график функции y = 1/x³ (1 делить на x в 3-ей степени (в кубе)) онлайн. Таблица точек.

График функции y = 1/x³ (1 делить на x в 3-ей степени (в кубе))

Интервалы задаются через точку с запятой (; ). При задании интервалов и шага можно использовать математические выражения (прим. -4pi; (5/6)pi) или слово «авто» или оставить поля пустыми (эквивалентно «авто»)

Округление:

Таблица точек функции f(x) = 1/x^3

Показать/скрыть таблицу точек

x	f(x)
-10	-0
-9.5	-0
-9	-0
-8.5	-0
-8	-0
-7.5	-0
-7	-0
-6.5	-0
-6	-0
-5.5	-0.01
-5	-0.01
-4.5	-0.01
-4	-0.02
-3.5	-0.02
-3	-0.04
-2.5	-0.06
-2	-0.13
-1.5	-0.3
-1	-1
-0.5	-8
0	отсутствует: деление на 0
0	-8
0.5	8
1	1
1.5	0.3
2	0.13
2.5	0.06
3	0.04
3.5	0.02
4	0.02
4.5	0.01
5	0.01
5.5	0.01
6	0
6.5	0
7	0
7.5	0
8	0
8.5	0
9	0
9.5	0
10	0

График построен по уравнению, но можно воспользоваться таблицой точек, чтобы построить такой же график по точкам.

Чтобы скачать график, нажмите на кнопку ‘Скачать график’ под ним.

Математические выражения

Для написания математических выражений доступно следующее:

Функции

Операторы

x^(1/n) — корень n-ой степени от числа x. То есть 8^(1/3) = 3 √8 = 2

Источник

Справочник по математике для самостоятельной работы студентов по теме «Виды функций и их графики»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»

Построение графиков функции, геометрические преобразования графиков функций, исследование графиков функций, графический метод решения уравнений

СОДЕРЖАНИЕ

y = x 2

y = x 3

Степенная функция

Показательная функция

Функция y = e x

Логарифмическая функция

Натуральный логарифм. y = ln x

Тригонометрические функции

arcsin

arccos

arcctg

Преобразования графиков функций

Симметричные преобразования

Параллельный перенос

Сжатие и растяжение

Построение графика функции y=|f(x)|

Построение графика функции y=f(|x|)

Обратное преобразование графика функции

Некоторые алгоритмы построения и свойства графиков функций

Построение графиков функций у = sin kx и y = cos kx

Линейная функция

Линейная функция — это функция вида:

здесь k и b являются действительными числами.

Линейная функция имеет следующие свойства:

1. y = kx + b — это ни чётная, ни нечётная функция;
2. Область определения функции y = kx + b — вся числовая прямая;
3. Множество значений лнейной функции — вся числовая прямая;
4. Если k > 0, то функция возрастает, а если k y = x 2

Функция игрек равен икс в квадрате имеет следующие свойства:

1. Функция y = x 2 — это четная функция, т.е. при изменении знака аргумента на противоположный, значение функции не меняется;
2. На промежутке от минус бесконечности до нуля функция игрек равен икс в квадрате убывает;
3. На промежутке от нуля до плюс бесконечности функция игрек равен икс в квадрате возрастает;
4. Область определения функции y = x 2 — вся числовая прямая;
5. Множество значений функции y = x 2 — от нуля до плюс бесконечности.

График функции y = x 2 называется парабола:

Функция игрек равен икс в кубе имеет следующие свойства:

1. Функция y = x 3 — это нечетная функция, т.е. при изменении знака аргумента на противоположный, значение функции меняется;
2. Функция игрек равен икс в кубе возрастает на всей числовой прямой;
3. Область определения функции y = x 3 — вся числовая прямая;
4. Множество значений функции y = x 3 — вся числовая прямая.

График функции y = x 3 называется кубическая парабола:

Функция y = x n называется степенной. Показатель степени n принадлежит множеству действительных чисел.

График степенной функции при том, что n натуральное и n больше или равно двум называется параболой n-й степени. Если n четное, то функция y = x n является четной, её график симметричен относительно оси ординат. Чем больше четное n, тем круче поднимаются вверх ветви параболы:

Степенная функция с целым отрицательным показателем y = x -n , где n четное и больше или равно двум, является четной, её график симметричен относительно оси ординат. Пример для y = x -2

Если n нечетное и n больше или равно трем, то функция y = x n является нечетной, её график симметричен относительно начала координат. Чем больше нечетное n, тем круче поднимаются вверх ветви параболы:

Степенная функция с целым отрицательным показателем y = x -n , где n нечетное и больше или равно трем, является нечетной, её график симметричен относительно начала координат. Пример для y = x -3 :

Показательная функция

Функция y = a x называется показательной, здесь a > 0 и a не равно 1.

Свойства показательной функции зависят от значения основания a.

Свойства показательной функции при a > 1:

1. Функция y = a x является ни четной, ни нечетной;
2. Функция игрек равен «а» в степени икс возрастает на всей числовой прямой;
3. Область определения функции y = a x — вся числовая прямая;
4. Область значений функции y = a x — промежуток от нуля до плюс бесконечности.

График функции y = a x при a = 2:

Свойства показательной функции при 0 x является ни четной, ни нечетной;
2. Функция игрек равен «а» в степени икс убывает на всей числовой прямой;
3. Область определения функции y = a x — вся числовая прямая;
4. Область значений функции y = a x — промежуток от нуля до плюс бесконечности.

График функции y = a x при a = 0,5:

Функция y = e x

Функция y = e x — это частный случай показательной функции. Основанием функции y = e x является иррациональное число e = 2.7182818284. Эта функция обладает характерной особенностью: касательная к графику функции y = e x в точке x = 0, y= 1 составляет угол 45 градусов с осью X.

График функции игрек равно «е» в степени икс:

Логарифмическая функция y = log_ax, т.е. логарифм икс по основанию а. Логарифмическая функция является обратной по отношению к показательной функции .

Свойства логарифмической функции зависят от значения основания a.

Свойства логарифмической функции при a > 1:

1. Функция y = log_ax является ни четной, ни нечетной;
2. Функция логарифм икс по основанию «а» возрастает на промежутке — от нуля до плюс бесконечности;
3. Область определения функции y = log_ax — интервал от нуля до плюс бесконечности;
4. Область значений функции y = log_ax — вся числовая прямая.

График функции y = log_ax при a = 2:

Свойства логарифмической функции при 0 Натуральный логарифм y = ln x.

Натуральный логарифм y = ln x, т.е. логарифм икс по основанию «e», является частным случаем обычного логарифма. Функция натуральный логарифм является обратной по отношению к функции y = e x .

Свойства натурального логарифма

1. Функция y = ln x является ни четной, ни нечетной;
2. Функция логарифм икс по основанию «e» возрастает на промежутке — от нуля до плюс бесконечности;
3. Область определения функции y = ln x — интервал от нуля до плюс бесконечности;
4. Область значений функции y = ln x — вся числовая прямая.

Тригонометрические функции: синус, косинус, тангенс, котангенс, аркфункции.

1. Функция синус y = sin x является нечетной;
2. y = sin x является возрастающей в интервале [0, П/2], в интервале [П/2, 3П/2] убывает, а в интервале [3П/2, 2П] вновь возрастает;
3. Область определения функции синус — вся числовая прямая;
4. Множество значений функции синус от -1 до 1;
5. Функция y = sin x является периодической с периодом 2Пи.

График функции y = sin x синусоида

1. Функция косинус y = cos x является четной;
2. y = cos x является убывающей в интервале [0, Пи], в интервале [Пи, 2Пи] возрастает, эти интервалы проходим против часовой стрелки;
3. Область определения функции косинус — вся числовая прямая;
4. Множество значений функции косинус от -1 до 1;
5. Функция y = cos x является периодической с периодом 2Пи.

График функции y = cos x косинусоида

1. Функция тангенс y = tg x является нечетной;
2. y = tg x возрастает в интервале [-Пи/2, Пи/2];
3. Область определения функции тангенс интервал [0, Пи], кроме точки Пи/2;
4. Множество значений функции тангенс — вся числовая прямая;
5. Функция y = tg x является периодической с периодом Пи.

График функции y = tg x тангенсоида, вертикальные линии на графике — это асимптоты тангенсоиды, т.е. графика функции y = tg x

Функция котангенс y = ctg x.

Свойства функции котангенс:

1. Функция котангенс y = ctg x является нечетной;
2. y = ctg x убывает в интервале [0, Пи];
3. Область определения функции котангенс интервал от нуля до Пи, кроме точек ноль и Пи;
4. Множество значений функции котангенс — вся числовая прямая;
5. Функция y = ctg x является периодической с периодом Пи.

На картинке график функции y = ctg x, вертикальные линии на графике — это асимптоты графика функции y = ctg x

Функция арксинус y = arcsin x. Функция arcsin является обратной для функции sin на отрезке -П/2 до П/2.

Свойства функции арксинус:

1. y = arcsin x является нечетной функцией;
2. Функция арксинус — возрастающая функция;
3. Область определения функции арксинус от -1 до 1;
4. Множество значений функции арксинус от -П/2 до П/2.

График функции y = arcsin x

Функция арккосинус y = arccos x. Функция arccos является обратной для функции cos на отрезке от 0 до Пи.

Свойства функции арккосинус:

1. y = arccos x является ни четной, ни нечетной функцией;
2. Функция арккосинус — убывающая функция;
3. Область определения функции арккосинус от -1 до 1;
4. Множество значений функции арккосинус от 0 до Пи.

График функции y = arccos x

Функция арктангенс y = arctg x. Функция arctg является обратной для функции tg на отрезке от -Пи/2 до Пи/2.

Свойства функции арктангенс:

1. y = arctg x является нечетной функцией;
2. Функция арктангенс — возрастающая функция;
3. Область определения функции арктангенс — вся числовая прямая;
4. Множество значений функции арктангенс от -П/2 до П/2.

График функции y = arctg x

Функция арккотангенс y = arcctg x. Функция arcctg является обратной для функции ctg на отрезке от 0 до Пи.

Свойства функции арккотангенс:

1. y = arcctg x является ни четной, ни нечетной функцией;
2. Функция арккотангенс — убывающей функция;
3. Область определения функции арккотангенс — вся числовая прямая;
4. Множество значений функции арккотангенс от 0 до Пи.

График функции y = arcctg x

Преобразования графиков функций

Определение. Преобразования графиков функций — это линейные преобразования функции y = f ( x ) или её аргумента x к виду y = af ( kx + b ) + m , а также преобразование с использованием модуля.

Зная, как строить графики функции y = f ( x ), где y = kx + b, y = ax 2 , y = x n , y = xk , y = sin x, y = cosx, y = tgx, y = ctgx, y = ax y = logax , можно построить график функции y = af ( kx + b ) + m.

Параллельный перенос графика вдоль оси абсцисс на| b |единиц

Параллельный перенос графика вдоль оси ординат на | m | единиц

Отражение графика

симметричное отражение графика относительно оси ординат.

симметричное отражение графика относительно оси абсцисс.

Сжатие и растяжение графика

При k > 1 — сжатие графика к оси ординат в k раз,

при 0 k — растяжение графика от оси ординат в k раз.

При k > 1 — растяжение графика от оси абсцисс в k раз,

при 0 k — сжатие графика к оси абсцисс в k раз.

Преобразования графика с модулем

При f ( x ) > 0 — график остаётся без изменений,

при f ( x ) — график симметрично отражается относительно оси абсцисс.

При — график остаётся без изменений,

при x — график симметрично отражается относительно оси ординат.

График функции y = -f(x) получается с помощью симметричного преобразования графика функции y = f(x) относительно оси х, при этом точка пересечения с осью х остается неизменной.

Рассмотрим данный вид преобразования на графике функции y = sin ( x )

Симметричным для графика y = sin(x) является график функции y = — sin(x)

Для более наглядного представления построим графики исходной функции и преобразованной в одной плоскости:

Рассмотрим данное преобразование на других примерах:

График функции y = f(x — a) получается с помощью переноса графика функции y =f (x) относительно оси х на вправо при а > 0 и влево при a 1) получается с помощью сжатия графика функции y = f(x) вдоль оси х в а раз.

Растяжение: График функции y=f(аx) (1 > a > 0) получается с помощью растяжения графика функции y = f(x) вдоль оси х в 1/а раз.

При этом в обоих случаях точки пересечения графика с осью у остаются неизменными

Рассмотрим данный вид преобразования на графике функции

С помощью растяжения графика на 2 получаем график функции y =/2

Для более наглядного представления построим графики исходной функции и преобразованной в одной плоскости:

Рассмотрим данные преобразование на других примерах:

Построение графика функции y=|f(x)|

Части графика y = f(x), лежащие выше оси х и на оси х, остаются без изменения, а лежащие ниже оси х — симметрично отражаются относительно этой оси (вверх)

Функция y = |f(x)| неотрицательна (её график расположен в верхней полуплоскости).

Рассмотрим функцию y = |x 2 — 4x + 3|

Рассмотрим данные преобразование на других примерах:

Построение графика функции y=f(|x|)

Часть графика y = f(x), лежащая левее оси у, удаляется, а часть, лежащая правее оси у остаётся без изменения и симметрично отражается относительно оси у (вверх)

Функция y = f(|x|) чётная (её график симметричен относительно оси у).

Рассмотрим функцию y = x 2 — |x| + 3

Рассмотрим данные преобразование на других примерах:

ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ГРАФИКА ФУНКЦИИ

График функции y = g(x), обратной функции y = f(x), можно получить преобразованием симметрии графика функции y = f(x) относительно прямой y = x.

Данное преобразование можно проводить только для функций, имеющих обратные.

Логарифмической функции обратна показательной

Квадратичной функции обратна y =:

Косинусу обратен арккосинус:

НЕКОТОРЫЕ АЛГОРИТМЫ ПОСТРОЕНИЯ И СВОЙСТВА ГРАФИКОВ ФУНКЦИЙ

D(y) = R; E(y) = [–1; 1];
Период: ; четная;
Возрастает: [–/2 + n; n]
Убывает: [n; /2 + n]
Нули функции:(/4 + 1/2n; 0)
Точки max: n;
Точки min: /2 + n;

Растянуть в 2 раза по оси ОХ.

D(y) = R; E(y) = [–1; 1];
Период: 4; четная;
Возрастает: [– 2 + 4n; 4n]
Убывает: [4n; 2 + 4n]
Нули функции:( + 2n; 0)
Точки max: 4n;
Точки min: 2 + 4n;

Сдвинуть график на 2 единицы влево по оси ОХ.

Сдвинуть график на 2 единицы вправо по оси ОХ.

Увеличить ординату в 2 раза.

Уменьшить ординату в 2 раза.

Выполнить зеркальное отображение относительно оси ОХ.

Сдвинуть график на 2 единицы вверх по оси Оy.

Сдвинуть график на 2 единицы вниз по оси Оy.

10. Алгоритм построения графика функции y =3 sin х

Построить график функции y=sinx

Осуществить растяжение от оси х с коэффициентом 3

11. Алгоритм построения графика функции y =-1/3 cosx -1

Построить график функции y=cosx

Осуществить сжатие к оси х с коэффициентом 3

Подвергнуть график преобразованию симметрии относительно оси х

Осуществить сдвиг вдоль оси у на 1 единицу масштаба вниз

12. Алгоритм построения графика функции y =-1/2 cosx

Построить график функции y=cosx

Осуществить сжатие к оси х с коэффициентом 2

Подвергнуть график преобразованию симметрии относительно оси х

Построить график функции y=sinx

Осуществить сдвиг вдоль оси x на π /6 единиц масштаба вправо

Осуществить растяжение от оси х с коэффициентом 4

Построение графиков функций

Для того чтобы построить графики функций у = sin kx и y = cos kx будет использован прием растяжения и сжатия графика по оси абсцисс. Этот прием часто применяется при построении графиков тригонометрических функций. Причём при 0 1, «сжимается». Построить график функции .

Для построения графика используем схему исследования функции, рассмотренную в предыдущем занятии.

Областью определения функции является вся числовая прямая. D(y) = R.

Множество значений функции промежуток [-1;1]. E(y) = [-1;1].

Функция нечетная, т.к. = — . График функции симметричен относительно начала координат.

Периодическая. Период данной функции найдем из равенства , где Т — наименьший положительный период для функции y = sinx, а k — коэффициент при аргументе (в данном случае ).

Найдем точки пересечения графика с осью Ох. Если у = 0, то = 0, откуда = k, x = 2k, а такими точками являются (0; 0), (2; 0), нам достаточно знать только эти точки, так как функция периодична и нечётна, и достаточно построить график только на отрезке [0; 2].

Максимум функции равен 1 при = , т. е. при х = .

Минимум функции равен -1 при = , т.е. при х = 3.
По этим данным построим график функции . Сначала график строим для положительного полупериода [0; 2], затем на отрезке, соответствующем отрицательному полупериоду [0; -2] (рис. 1), и, наконец, на всей области определения (штриховая линия).

Но график функции можно построить иначе, приняв за исходный известный нам график функции
у = sinx, нанесенный штриховой линией на рисунке 2. Замечаем, что период исходной функции y = sinx равен
T = 2, а период заданной функции составляет t = 4, т. е. вдвое больше периода исходной функции. Таким образом, график, который требуется построить, получится из исходного графика (штрихового, на рисунке 2) путем растяжения его вдоль оси Ох вдвое.

График функции y = sin 4x будем строить аналогично предыдущему, учитывая, что k = 4, период этой функции равен: . Область определения функции — вся числовая прямая. Множество значений — отрезок [-1; 1].
График функции у = sin 4х строим путем сжатия по оси Ох исходного графика y = sinx в 4 раза (рис. 3), так как период у заданной функции в 4 раза меньше периода 2 исходной функции.

Таким образом, если известен график y = f (x), то график функции y = f(kx) строится посредством сжатия по оси Ох исходного графика пропорционально коэффициенту k при аргументе, а именно: если k > 1, то сжатие в k раз; если 0 k раз.

Источник