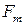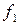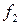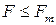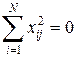Геометрическая интерпретация полного факторного эксперимента 2 в кубе

Теория Планирования Эксперимента

Главная

Полный факторный эксперимент

Первый этап планирования эксперимента для получения линейной модели основан на варьировании факторов на двух уровнях. В этом случае, если число факторов известно, можно сразу найти число опытов, необходимое для реализации всех возможных со­четаний уровней факторов. Простая формула, которая для этого используется, уже приводилась: 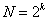, где N – число опытов, k – число факторов, 2 – число уровней. В общем случае эксперимент, в котором реализуются все­возможные сочетания уровней факторов, называется полным факторным экспериментом. Если число уровней каждого фактора равно двум, то имеем полный факторный экспе­римент типа 2 k .

Нетрудно написать все сочетания уровней в экспе­рименте с двумя факторами. Напомним, что в планиро­вании эксперимента используются кодированные значения факторов: +1 и –1 (часто для простоты записи единицы опускают). Условия эксперимента можно записать в виде таблицы, где строки соответствуют различным опытам, а столбцы – значениям факторов. Будем называть такие таблицы матрицами планирования эксперимента.

Матрица планирования для двух факторов приведена ниже

Каждый столбец в матрице планирования называют вектор-столбцом, а каждую строку – вектор-строкой. Таким образом, мы имеем 2 вектор-столбца независимых переменных и один вектор-столбец парамет­ра оптимизации.

Если для двух факторов все возможные комбинации уровней легко найти прямым перебором (или просто запомнить), то с ростом числа факторов возникает необ­ходимость в некотором приеме построения матриц. Из многих возможных обычно используется три приема, основанные на переходе от матриц меньшей размерности к матри­цам большей размерности. Рассмотрим первый. При добав­лении нового фактора каждая комбинация уровней исход­ного плана встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Отсюда естественно появляется прием: записать исходный план для одного уровня нового фактора, а затем повторить его для другого уровня. Вот как это выглядит при переходе от экспери­мента 2 2 к 2 3 :

Этот прием распространяется на построение матриц любой размерности.

Рассмотрим второй прием. Для этого введем правило перемножения столбцов матрицы. При построчном перемно­жении двух столбцов матрицы произведение единиц с одноименными знаками дает +1, а с разноименными –1. Воспользовавшись этим правилом, получим для случая, который мы рассматриваем, вектор-столбец произведения x ₁ x ₂ в исходном плане. Далее повторим еще раз исходный план, а у столбца произведений знаки поменяем на обрат­ные. Этот прием тоже можно перенести на построение матриц любой размерности, однако он сложнее, тем первый.

Третий прием основан на правиле чередования знаков. В первом столбце знаки меняются поочередно, во втором столбце они чередуются через два, в третьем – через 4, в четвертом – через 8 и т. д. по степеням двойки.

Свойства полного факторного эксперимента типа 2 k

Мы научились строить матрицы планирования полных факторных экспериментов с факторами на двух уровнях. Теперь выясним, какими общими свойствами эти матрицы обладают независимо от числа факторов. Говоря о свойствах матриц, мы имеем в виду те из них, которые определяют качество модели. Ведь эксперимент и плани­руется для того, чтобы получить модель, обладающую некоторыми оптимальными свойствами. Это значит, что оценки коэффициентов модели должны быть наилучшими и что точность предсказания параметра оптимизации не должна зависеть от направления в факторном пространстве, ибо заранее неясно, куда предстоит двигаться в поисках оптимума.

Два свойства следуют непосредственно из построения матрицы. Первое из них – симметричность относительно центра эксперимента – формулируется следующим образом: алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю, или, где j – номер фактора, N – число опытов, i = 1, 2, . k .

Второе свойство – так называемое условие нормировки – формулируется следующим образом: сумма квадратов элементов каждого столбца равна числу опытов, или 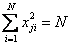. Это следствие того, что значения факторов в матрице задаются +1 и –1.

Это свойства отдельных столбцов матрицы планирования. Теперь остановимся на свойстве совокупности столбцов. Сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю, или

Это важное свойство называется ортогональностью матрицы планирования.

Последнее, четвертое свойство называется ротатабельностью, т. е. точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления.

Полный факторный эксперимент и математическая модель

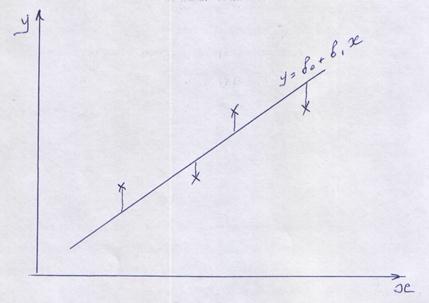
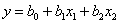
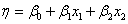
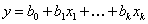
Для движения к точке оптимума нам нужна линейная модель . Наша цель – найти по результатам эксперимента значения неизвестных коэффициентов модели. До сих пор, говоря о линейной модели, мы не останавливались на важном вопросе о статистической оценке ее коэффициентов. Теперь необходимо сделать ряд замечаний по этому поводу. Можно утверждать, что эксперимент проводится для проверки гипотезы о том, что линейная модель адекватна. Греческие буквы использованы для обозначения «истинных» генеральных значений соответствующих неизвестных. Эксперимент, содержащий конечное число опытов, позволяет только получить выборочные оценки для коэффициентов уравнения . Их точность и надежность зависят от свойств выборки и нуждаются в статистической проверке. Как производится такая проверка, будет показано ниже. А пока займемся вычислением оценок коэффициентов. Их можно вычислить по простой формуле

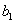
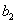
обоснование которой будет приведено ниже. Воспользуемся этой формулой для подсчёта коэффициентов и :

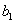
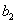
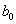
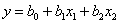
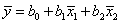
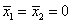
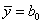
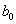
Благодаря кодированию факторов расчет ко­эффициентов превратился в простую арифметическую про­цедуру. Для подсчета коэффициента используется вектор-столбец х₁, а для – столбец x ₂ . Остается неясным, как найти . Если уравнение справедливо, то оно верно и для средних арифметических значений переменных: . Но в силу свойства симметрии . Следовательно, . Мы пока­зали, что есть среднее арифметическое значений пара­метра оптимизации. Чтобы его получить, необходимо сло­жить все y и разделить на число опытов. Чтобы привести, эту процедуру в соответствие с формулой для вычисления коэффициентов, в матрицу планирования удобно ввести вектор-столбец фиктивной переменной x ₀ , которая прини­мает во всех опытах значение +1. Это было уже учтено в записи формулы, где j принимало значения от 0 до k .

Теперь у нас есть все необходимое, чтобы найти неизвестные коэффициенты линейной модели

Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше численная величина коэффициента, тем большее влияние оказывает фактор. Если коэффициент имеет знак плюс, то с увеличением зна­чения фактора параметр оптимизации увеличивается, а если минус, то уменьшается. Величина коэффициента соответ­ствует вкладу данного фактора в величину параметра опти­мизации при переходе фактора с нулевого уровня на верх­ний или нижний.

Иногда у добно оценивать вклад фактора при переходе от нижнего уровня к верхнему уровню. Вклад, определенный таким образом, называется вкладом фактора (иногда его называют основным или главным эффектом). Он численно равен удвоенному коэффициенту. Для качественных факторов, варьируемых на двух уровнях, основной уровень не имеет физического смысла. Поэтому понятие «эффект фактора» является здесь естественным.

Планируя эксперимент, на первом этапе мы стремимся получить линейную модель. Однако у нас нет гарантии, что в выбранных интервалах варьирования процесс описывается линейной моделью. Существуют способы проверки пригодности линейной модели (проверка адекватности). А если модель нелинейна, как количественно оценить нелинейность, пользуясь полным факторным экспериментом?

Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор. В этом случае гово­рят, что имеет место эффект взаимодействия двух факторов. Полный факторный эксперимент позволяет количественно оценивать эффекты взаимодействия. Для этого надо, пользуясь правилом перемножения столбцов, получить стол­бец произведения двух факторов. При вычислении коэффициента, соответствующего эффекту взаимодействия, с новым вектор-столбцом можно обращаться так же, как с вектор-столбцом любого фактора. Для полного факторного эксперимента 2 2 матрица планирования с учетом эффекта взаимодействия будет иметь вид

Источник

Полный факторный эксперимент (ПФЭ)

3.5.1. Матрица планирования эксперимента. Её свойства.

В ПФЭ каждый фактор варьируется на двух уровнях. Число возможных комбинаций уровней факторов будет:

Таким образом, эксперимент, в котором реализуются все возможные комбинации уровней факторов, называют полным факторным экспериментом.

Условия эксперимента удобно представлять в виде таблицы, называемой матрицей планирования или планом эксперимента, который включает «собственно план» и вспомогательные столбцы, служащие для обработки уже проведённого эксперимента.

При большом числе опытов и факторов удобно пользоваться следующим правилом для составления матрицы планирования ПФЭ: в первом столбце х₁ знаки «плюс» и «минус» меняются поочередно; во втором х₂ – через два; в третьем –через четыре; в четвертом – через восемь и т.д. Матрица планирования эксперимента 2 3 c эффектами взаимодействия имеет вид, приведенный в табл. 3.2.

№ опыта	х0	х 1	х 2	х 3	х 1 х 2	х 1 х 3	х 2 х 3	х 1 х 2 х 3	yi
+	+	+	+	+	+	+	+	y 1
+	–	+	+	–	–	+	–	y2
+	+	–	+	–	+	–	–	y3
+	–	–	+	+	–	–	+	y4
+	+	+	–	+	–	–	–	y5
+	–	+	–	–	+	–	+	y6
+	+	–	–	–	–	+	+	y7
+	–	–	–	+	+	+	–	y8
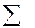	N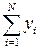

Построенный таким образом план ПФЭ обладает свойствами:

· симметричности относительно центра эксперимента – сумма элементов каждого столбца равна нулю

; (3.13)

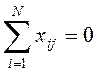
· нормировки – сумма квадратов элементов каждого столбца равна числу опытов

; (3.14)

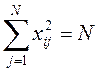
· ортогональности – сумма построчных произведений элементов двух любых столбцов равна нулю

, . (3.15)

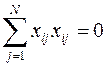
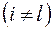
Ортогональность является важным свойством планов ПФЭ, поскольку оценка всех коэффициентов уравнения регрессии производится независимо друг от друга и факторы, имеющие незначимые коэффициенты могут быть выведены из состава уравнения без повторного вычисления остальных коэффициентов уравнения регрессии;

· ротабельности, которая означает одинаковость предсказательной способности уравнений, полученных по планам ПФЭ по всем направлениям от начала координат, т.е. дисперсия предсказания зависит только от радиуса сферы, на которой расположена рассматриваемая точка.

Указанные выше свойства планов ПФЭ существенно упрощают расчетные формулы по определению оценок коэффициентов линейных моделей.

Геометрически матрица планирования представляет квадрат, куб, k –мерный гиперкуб, в зависимости от числа факторов, в котором вершины являются опытными точками.

Рис. 3.2. Геометрическая интерпретация матрицы планирования 2 2 .

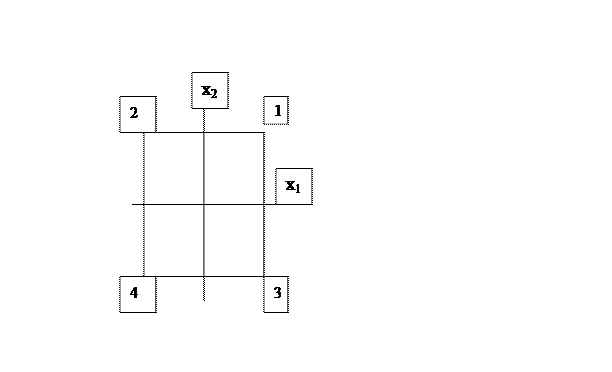
В общем случае линейная модель имеет вид

. (3.16)

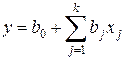
3.5.2. Метод наименьших квадратов. Оценка коэффициентов модели.

Поскольку при проведении ПФЭ число опытов определяется величиной N=2 k , то для идентификации четырехфакторной линейной модели, которая содержит 5 неизвестных коэффициентов, необходимо провести 16 опытов. В этом случае число уравнений, которые можно составить после проведения опытов по плану ПФЭ, превышает число неизвестных коэффициентов. С целью снятия переопределенности системы для вычисления коэффициентов полинома используют метод наименьших квадратов (МНК). Идея МНК состоит в том, что оценки коэффициентов линейного уравнения выбираются из условия минимизации ошибки аппроксимации .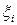

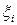
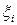
Пусть y_i действительное значение функции отклика, определяемое в i–том опыте, а y_0i – значение, рассчитанное по формуле (3.16). Ошибка определится как разность действительного и расчётного значений функции отклика =y_i – y_0i.

Оценки коэффициентов уравнения регрессии (3.16) определяются из условия

. (3.17)

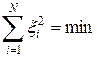
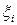
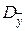
Предположим, что ошибки в отдельных наблюдениях имеют нормальное распределение с нулевым математическим ожиданием и одинаковой дисперсией , не коррелированны между собой и не зависят от значений факторов. Для простоты математических выкладок рассмотрим однофакторный эксперимент. Модель в этом случае имеет вид:

Запишем условие (17) для рассматриваемого случая

. (3.19)

Минимум выражения (3.19) может быть достигнут за счет подборакоэффициентов b₀ и b₁. Это означает, что частные производные выражения (3.19) по неизвестным коэффициентам должны быть равны нулю.

.(3.20)

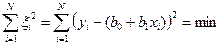
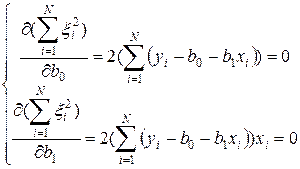
Проведя несложные преобразования, получим систему линейных уравнений относительно неизвестных коэффициентов полинома:

. (3.21)

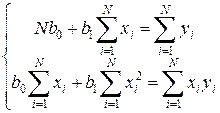
Число уравнений в системе (3.21) равно числу двух искомых коэффициентов b₀ и b_1.

Исходя из свойств симметричности 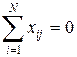и нормировки

систему (3.21) можно переписать

. (3.22)

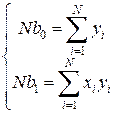
Откуда могут быть получены оценки коэффициентов полинома

, . (3.23)

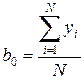
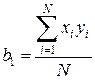
Формулы для определения оценок коэффициентов линейной модели в случае действия k факторов можно привести к единому виду, если в матрицу планирования ввести нулевой столбец, состоящий из верхних уровней нормированных факторов, т.е. +I (см. табл. 3.2). Тогда выражение для j коэффициента примет вид:

, (3.24)

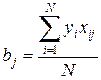
где j– номер коэффициента, стоящего при соответствующем факторе (j=0,1. k);

Таким образом, способ расчета коэффициентов модели в данном случае очень прост: для подсчета любого b_jстолбцу результатов эксперимента y_i следует приписать знаки соответствующего столбца x_j,, сложить экспериментально найденные значения y_i с этими знаками и результат разделить на число опытов матрицы планирования.

При ортогональном планировании формула для определения коэффициентов принимает вид:

. (3.25)

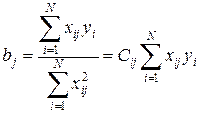
Поскольку коэффициенты регрессии рассчитывают по формуле (3.25) из результатов опытов, являющихся случайными величинами, то и сами коэффициенты является случайными величинами.

3.5.3. Оценка значимости коэффициентов модели.

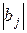
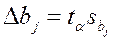
После нахождения оценок коэффициентов производится оценка их значимости, которая проводится путёмсопоставления абсолютной величины коэффициента с его доверительным интервалом его определения, рассчитываемым по формуле:

; (3.26)

где t_α –значение критерия Стьюдента, который берется изтаблиц его распределения в зависимости от уровня значимости α (α = 0,01; 0,05; 0,1) и числа степеней свободы f₁= n₀ — 1 (где n₀ –число дублирующих опытов, обычно, в центре плана). Для технических измерений α чаще всего принимается равным 0,05. Для меньших значений величины α доверительный интервал определения получается больше (см. табл. 3.3).

– среднеквадратичная ошибка в определении коэффициента регрессии b_j, которая определяется в зависимости от величины дисперсии воспроизводимости.

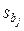
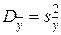
В случае равномерного дублирования опытов и числе дублирующих опытов в каждой строке плана n дисперсия коэффициентов определяется по формуле

. (3.27)

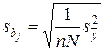
Коэффициент считается статистически значимым, когда его абсолютная величина больше доверительного интервала его определения или равна ему

или ; (3.28)

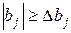
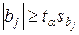
Смысл последнего неравенства заключается в том, что абсолютная величина значимого коэффициента должна быть в 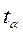раз больше, чем ошибка его определения.

Некоторые значения критерия Стьюдента 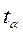приведены в табл. 3.3.

Число степеней свободы f1	Уровни значимости α
0,1	0,05	0,01
I	6,3I	12,7	63,66
2,92	4,30	9,93
2,02	2,57	4,03
1 ,81	2,23	3,17
1,73	2,03	2,85
1,64	1,96	2,58

Статистическая незначимость коэффициента в уравнении 3.16 интерпретируется, как отсутствие влияния соответствующего фактора. Если модель линейная и соответственно незначим линейный эффект, можно считать, что данный фактор в изученных интервалах его изменения на функцию отклика не влияет.

При ортогональном планировании статистически незначимые коэффициенты из модели могут быть исключены и при этом пересчет остальных коэффициентов не требуется.

3.5.4. Оценка адекватности модели

После оценивания коэффициентов модели проводится оценка адекватности модели, которая состоит в оценке однородности дисперсии воспроизводимости и дисперсии неадекватности с использованием критериев, приведенных в разделе 3.3.

Дисперсию неадекватности определяют по формуле (3.29)

, (3.29)

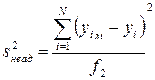
где – значение у, определенное по модели для i-тых условий

– значение у, определенное в i-том опыте;

– число степеней свободы определения дисперсии неадекватности.

, (3.30)

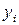
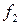
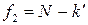
где 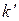– число найденных коэффициентов в модели.

При оценке адекватности модели по критерию Фишера оценивается отношение

, (3.31)

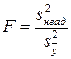
которое сопоставляется с табличным значением , определяемом при степени свободы дисперсии воспроизводимости и степени свободы дисперсии неадекватности . Если , то модель считается адекватной, в противном случае модель неадекватна.

Источник