Дана длина ребра куба 5 найти его объем

Клёвый код

Решаем задачи Абрамян на C. Matrix78

Matrix78. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их минимальные элементы образовывали убывающую последовательность.

Решаем задачи Абрамян на C. Matrix77

Matrix77. Дана матрица размера $$M \times N$$. Упорядочить ее столбцы так, чтобы их последние элементы образовывали убывающую последовательность.

Решаем задачи Абрамян на C. Matrix76

Matrix76. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их первые элементы образовывали возрастающую последовательность.

Решаем задачи Абрамян на C. Matrix75

Matrix75. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным максимумом, если он больше всех окружающих его элементов. Поменять знак всех локальных максимумов данной матрицы на противоположный. При решении допускается использовать вспомогательную матрицу.

Решаем задачи Абрамян на C. Matrix74

Matrix74. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным минимумом, если он меньше всех окружающих его элементов. Заменить все локальные минимумы данной матрицы на нули. При решении допускается использовать вспомогательную матрицу.

Решаем задачи Абрамян на C. Matrix73

Matrix73. Дана матрица размера $$M \times N$$. После последнего столбца, содержащего только отрицательные элементы, вставить столбец из нулей. Если требуемых столбцов нет, то вывести матрицу без изменений.

Решаем задачи Абрамян на C. Matrix72

Matrix72. Дана матрица размера $$M \times N$$. Перед первым столбцом, содержащим только положительные элементы, вставить столбец из единиц. Если требуемых столбцов нет, то вывести матрицу без изменений.

Решаем задачи Абрамян на C. Matrix71

Matrix71. Дана матрица размера $$M \times N$$. Продублировать столбец матрицы, содержащий ее минимальный элемент.

Решаем задачи Абрамян на C. Matrix70

Matrix70. Дана матрица размера $$M \times N$$. Продублировать строку матрицы, содержащую ее максимальный элемент.

Решаем задачи Абрамян на C. Matrix69

Matrix69. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. После столбца матрицы с номером $$K$$ вставить столбец из единиц.

Источник

Решение задач. День первый. Задачи Begin1-10

Итак, с сегодняшнего дня мы начинаем вести новую рубрику: «Решение задач», в которой будем рассматривать задачи, взятые из сборника М.Э.Абрамяна «1000 ЗАДАЧ ПО ПРОГРАММИРОВАНИЮ».

Открыв задачник и прочитав аннотацию, Вы, скорее всего, озадачитесь тем, что данное пособие предназначено для студентов механико-математического, физического и экономического факультетов, но смею Вас заверить, что это весьма универсальная книга, которая подходит как студентам, так и школьникам. Возможно, задачи из первых разделов книги покажутся Вам простыми — в этом случае используйте наш разбор только для проверки своих решений; но если же по каким-либо причинам решить задачи Вы не в состоянии, то тогда присоединяйтесь к нам.

Begin1. Дана сторона квадрата a. Найти его периметр P = 4·a.

Прежде всего напомню, что для ввода и вывода информации, в Паскале используют следующие операторы:

• Read (Readln) — ввод значений с клавиатуры;
• Write (Writeln) — вывод результата (и вообще чего-либо) на экран.

Блок-схема

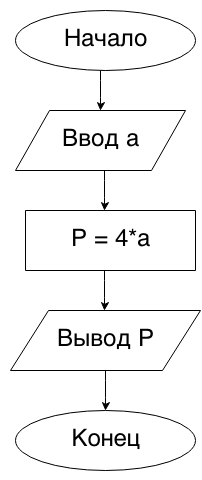
Таким образом, решение задачи становится очевидным.

Begin2. Дана сторона квадрата a. Найти его площадь S = a 2 .
При решении данной задачи воспользуемся функцией sqr . Можно, конечно, вычислять квадрат, умножая число само на себя (S=a*a), но при вводе действительно больших чисел наша программа будет выполняться гораздо дольше, нежели при использовании sqr .

Begin3°. Даны стороны прямоугольника a и b. Найти его площадь S = a·b и периметр P = 2·(a + b).

Да, задача по сути своей проста и подобна предыдущим, поэтому поскорее составим к ней решение и перейдем к следующей.

Begin4. Дан диаметр окружности d. Найти ее длину L = π·d. В качестве значения π использовать 3.14.

У вас, наверняка, возникает вопрос π — это константа или переменая? Так как π не изменяется в течение программы, π — константа. Вообще в Паскале уже встроена такая константа, но ее значение:

А так как в условии задачи указано, что в качестве значения π нужно использовать 3.14, то следует объявить π в разделе описания констант.

Begin5. Дана длина ребра куба a. Найти объем куба V = a 3 и площадь его поверхности S = 6·a 2 .

Для решения задачи используем функцию power(x, a), где a — степень, x — число возводимое в степень (разумеется, использовать ее мы будем только для возведения числа в третью степень, квадрат числа по-прежнему находим с помощью sqr(x) ).

Begin6. Даны длины ребер a, b, c прямоугольного параллелепипеда. Найти его объем V = a·b·c и площадь поверхности S = 2·(a·b + b·c + a·c).

Begin7°. Найти длину окружности L и площадь круга S заданного радиуса R:
L = 2·π·R, S = π·R 2 .
В качестве значения π использовать 3.14.

Begin8. Даны два числа a и b. Найти их среднее арифметическое: (a + b)/2.

Begin9. Даны два неотрицательных числа a и b. Найти их среднее геометрическое, то есть квадратный корень из их произведения: √(a*b).

Напомню, что для нахождения квадратного корня мы используем функцию sqrt .

Begin10. Даны два ненулевых числа. Найти сумму, разность, произведение и частное их квадратов.

Ну вот и все. Следующая публикация с решением задач выйдет в ближайшие дни.

Источник

Объемы фигур. Объем куба.

Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте).

У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны.

Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна

ширине и равна высоте, то объем куба равен s 3 ,

где s – длина одного (любого) ребра куба.

Воспользуйтесь онлайн калькулятором для расчета объема куба: объем куба, онлайн расчет.

Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.

Метод 1 из 3: Возведение в куб ребра куба

• Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы

вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.

Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.

Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза.

Если s — длина ребра куба, то

и, таким образом, вы вычислите объем куба.

Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на

ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть,

другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и

равна высоте, то это процесс можно заменить возведением ребра куба в третью степень.

В нашем примере объем куба равен:

• К ответу припишите единицы измерения объема. Так как объем – это количественная

характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические

В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических

сантиметрах (или в см 3 ). Итак, объем куба равен 125 см 3 .

Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих

Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м 3 .

Метод 2 из 3: Вычисление объема по площади поверхности

• В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых вы

можете найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите

ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем

возведите длину ребра куба в третью степень и вычислите объем куба.

Площадь поверхности куба равна 6s 2 ,

где s – длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так

как у куба 6 равных граней).

Рассмотрим пример. Площадь поверхности куба равна 50 см 2 . Найдите объем куба.

• Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь

одной грани куба). В свою очередь площадь одной грани куба равна s 2 , где s – длина ребра куба.

В нашем примере: 50/6 = 8,33 см 2 (не забывайте, что площадь измеряется в квадратных единицах — см 2 ,

• Так как площадь одной грани куба равна s 2 , то извлеките квадратный корень из значения площади

одной грани и получите длину ребра куба.

В нашем примере, √8,33 = 2,89 см.

• Возведите в куб полученное значение, чтобы найти объем куба.

В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см 3 . К ответу не забудьте приписать кубические

Метод 3 из 3: Вычисление объема по диагонали

• Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом,

если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив

Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба

равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см 3 .

где d — диагональ грани куба, s – ребро куба. Эта формула вытекает из теоремы Пифагора, согласно

которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен

сумме квадратов катетов (в нашем случае ребер), то есть:

• Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче

дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3.

Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный

(где D — диагональ куба, s – ребро куба).

Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае

диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет –

это ребро, а второй катет – это диагональ грани куба, равная 2s 2 ), то есть

Рассмотрим пример. Диагональ куба равна 10 м. Найдите объем куба.

Источник

Нахождение объема куба: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.

Формула вычисления объема куба

1. Через длину ребра

Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.

V = a ⋅ a ⋅ a = a 3

2. Через длину диагонали грани

Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√ 2 .

Следовательно, вычислить объем куба можно так:

Примеры задач

Задание 1
Вычислите объем куба, если его ребро равняется 5 см.

Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .

Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.

Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:

Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.

Решение:
Применим формулу, в которой используется диагональ грани:

Источник