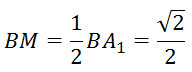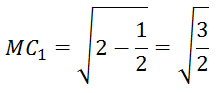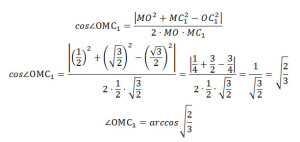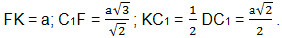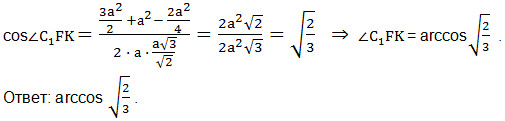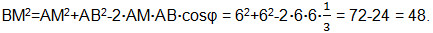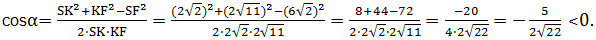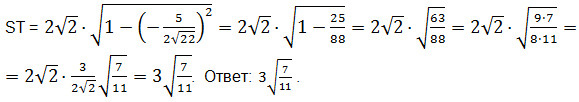Дан куб найти угол между плоскостями ва1с1

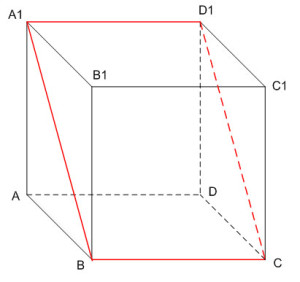
Задание 14. Математика ЕГЭ. Дан куб ABCDA1B1C1D1. Найдите угол между плоскостями BA1C1 и BA1D1.

а) Постройте сечение куба плоскостью, проходящей через точки B, A₁ и D₁.

б) Найдите угол между плоскостями BA₁C₁ и BA₁D₁.

Построим плоскость, проходящую через точки B, A₁ и D₁, т. е. плоскость BA₁D₁. Точки B и A₁ лежат в одной плоскости, поэтому можно провести прямую BA₁. Так как ВС параллельна A₁D₁, то точка С лежит в плоскости BA₁D₁. Точки С и D₁ лежат в одной плоскости, поэтому можно провести прямую СD₁. Прямоугольник BA₁D₁С – искомое сечение.

Построим плоскость BA₁C₁. Точки B и A₁ лежат в одной плоскости, проведем прямую BA₁. Точки A₁ и C₁ лежат в одной плоскости, проведем прямую A₁C₁. Точки B и C₁ лежат в одной плоскости, проведем прямую BC₁. Треугольник BA₁C₁ – искомое сечение. Так как сторонами этого треугольника являются диагонали граней куба, то треугольник BA₁C₁ – равносторонний треугольник.

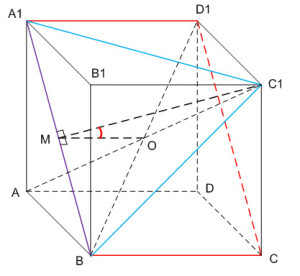
Найдем угол между плоскостями BA₁C₁ и BA₁D₁. Плоскости BA₁C₁ и BA₁D₁ пересекаются по прямой BA₁. Отрезок C₁М – высота и медиана треугольника BA₁C₁, т.е. отрезок C₁М перпендикулярен BA₁, а также точка М – середина BA₁. Найдем точку пересечения диагоналей куба, получим точку О – центр куба. Отрезок МО – средняя линия треугольника BA₁D₁. Так как A₁D₁ перпендикулярен BA₁, а A₁D₁ II MO, то МО перпендикулярен BA₁.

Следовательно, угол ∠ОМC₁ является линейным углом двугранного угла, образованного плоскостями BA₁C₁ и BA₁D₁. Угол ∠ОМC₁ – искомый угол между плоскостями BA₁C₁ и BA₁D₁. Найдем величину этого угла. Углом между двумя плоскостями называется величина острого двугранного угла.

Рассмотрим треугольник ОМC₁, найдем стороны этого треугольника. Пусть ребро куба равно 1. МО – средняя линия треугольника BA₁D₁, тогда МО = 1/2.

Треугольник ВСС₁ – прямоугольный (∠С = 90°), по тереме Пифагора

Треугольник ВМС₁ – прямоугольный (∠М = 90°):

Найдем ОС₁, диагональ куба AC₁ = √3, тогда ОС₁ = √3/2.

По теореме косинусов найдем cos∠ОМC₁:

Так как за величину угла между двумя плоскостями берется величина острого двугранного угла (взят модуль), получим

Источник

ЕГЭ ФИПИ-2015, задача 16 (варианты 11, 12, 13)

а) Постройте сечение куба плоскостью, проходящей через точки В, А₁ и D₁.

б) Найдите угол между плоскостями BA₁C₁ и BA₁D₁.

Решение.

а) Так как секущая плоскость пересекает верхнюю грань по ребру A₁D₁ , то и нижнюю грань она пересечет по прямой, проходящей через точку В и параллельной A₁D₁, т.е. по прямой ВС. Таким образом, прямоугольник A₁D₁СВ – плоскость сечения.

В равностороннем ∆ A₁C₁В отрезок C₁F – высота. Если ребро куба обозначить через а, то

Точку F соединим с точкой К – центром квадрата BC₁D₁D ( задней грани куба). FK⊥А₁В. Почему? Так как FK – отрезок, соединяющий центры передней и задней граней, то он будет перпендикулярен каждой из этих граней, а значит, будет перпендикулярен и отрезку А₁В. Отрезок FK будет параллелен и равен ребрам ВС и A₁D₁, т.е. FK=a.

Угол С₁FК – линейный угол между плоскостями BA₁C₁ и BA₁D₁. Обозначим этот угол через α. Рассмотрим треугольник С₁FК. Имеем:

По теореме косинусов найдем косинус угла С₁FК.

Подставим все имеющиеся значения в (*).

В правильной четырёхугольной пирамиде SABCD основание ABCD – квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка М так, что АM=6.

а) Постройте перпендикуляр из точки S на плоскость BCM.

б) Найдите расстояние от вершины S до плоскости BCM.

Решение.

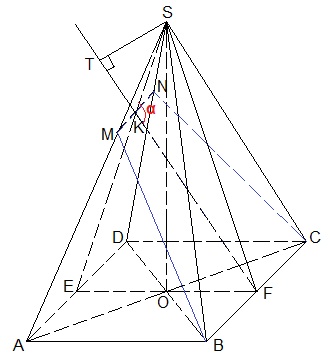
Смотрите задачи вариантов 1 и 7. Чертеж чуть отличается, так как точка М делит боковое ребро на отрезки 6 и 3 (по условию АМ=6). Рассуждения те же.

а) Сечение пирамиды проходящее через точки В,С и М представляет собой равнобокую трапецию BMNC, KF – ось трапеции. Перпендикуляр из точки S на плоскость BCM — высота ∆SKF. В зависимости от угла SKF эта высота может лежать внутри ∆SKF или вне ∆SKF. Обозначим SKF через α и определим угол α из теоремы косинусов. Для этого нужно знать все стороны ∆SKF.

Так же нужно определить угол φ при основании каждой боковой грани пирамиды.

Рассмотрим грань SAD.

В ∆МАВ на основании теоремы косинусов имеем:

Рассмотрим равнобедренную трапецию BMNC. Проведем МР⏊ВС. Так как МК=1,то PF=1 ⇒ BP=3-1=2. Из ∆BPM находим:

Наконец, из ∆SKF определяем косинус угла α:

Итак, cosα

а) Постройте сечение куба плоскостью, проходящей через точки В, А₁ и D₁.

б) Найдите угол между плоскостями АВ₁C₁ и BA₁D₁.

Решение.

а) Так как секущая плоскость пересекает параллельные плоскости по параллельным прямым, то плоскость BA₁D₁ пересечет основание по прямой ВС, и искомое сечение – BA₁D₁C.

б) Аналогично строим плоскость AB₁C₁D.

Эти плоскости пересекаются по прямой ОО₁, точки О и О₁ – центры квадратов (передней и задней граней куба). Отрезок ОО₁ перпендикулярен граням АА₁В₁В и DD₁C₁D, следовательно ОО₁⊥АВ₁ и ОО₁⊥А₁В. Угол между диагоналями АВ₁ и А₁В квадрата и есть угол между плоскостями АВ₁C₁ и BA₁D₁. Мы знаем, что диагонали квадрата взаимно перпендикулярны, следовательно, угол между плоскостями АВ₁C₁ и BA₁D₁ равен 90 0 .

Источник

Презентация по математике «Угол между плоскостями»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

ДВУГРАННЫЙ УГОЛ. УГОЛ МЕЖДУ ПЛОСКОСТЯМИ Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой. Линейным углом двугранного угла называется угол, образованный лучами с вершиной на граничной прямой, стороны которого лежат на гранях двугранного угла и перпендикулярны граничной прямой. Величиной двугранного угла называется величина его линейного угла. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.

В кубе A…D1 найдите угол между плоскостями ABC и CDD1. Ответ: 90o.

В кубе A…D1 найдите угол между плоскостями ABC и CDA1. Ответ: 45o.

В кубе A…D1 найдите угол между плоскостями ABC и BDD1. Ответ: 90o.

В кубе A…D1 найдите угол между плоскостями ABC и BC1D.

В кубе A…D1 найдите угол между плоскостями ABC и BC1D. Решение: Обозначим O середину BD. Искомым линейным углом будет угол COC1. В прямоугольном треугольнике COC1 имеем CC1 = 1; CO = Следовательно,

В кубе A…D1 найдите угол между плоскостями ABC и AB1D1.

В кубе A…D1 найдите угол между плоскостями ACC1 и BDD1. Ответ: 90o.

В кубе A…D1 найдите угол между плоскостями ABC1 и BB1D1.

В кубе A…D1 найдите угол между плоскостями ABC1 и BB1D1. Решение: Заметим, что плоскость равностороннего треугольника ACB1 перпендикулярна диагонали BD1, которая проходит через центр O этого треугольника. Искомым линейным углом будет угол B1OE, который равен 60o. Ответ: 60o.

В кубе A…D1 найдите угол между плоскостями BC1D1 и BA1D. Ответ: 90o. Решение: Заметим, что плоскость равностороннего треугольника BDA1 перпендикулярна диагонали AC1, которая проходит через центр этого треугольника. Следовательно, данные плоскости перпендикулярны. Искомый угол равен 90o.

В кубе A…D1 найдите угол между плоскостями BC1D и BA1D.

В кубе A…D1 найдите угол между плоскостями BC1D и BA1D. Решение: Пусть O – середина BD. Искомый угол равен углу A1OC1. Имеем Используя теорему косинусов, получим Ответ:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 595 601 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Добавить в избранное

• 28.09.2016 16052
• PPTX 247 кбайт
• 79 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Покотилова Александра Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Школы смогут вносить данные в портфолио школьника в «МЭШ»

Минпросвещения упростит процедуру подачи документов в детский сад

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник