Что такое треугольный куб

Как собирать треугольный кубик Рубика — описание, схемы и рекомендации

Головоломки – это не только развлечение, но и хорошая зарядка для ума. Классический кубик Рубика появился еще в 1974 году. Однако его до сих пор с удовольствием собирают и взрослые, и дети. Но мало кто знает, что есть еще одна схожая головоломка – треугольный кубик Рубика, он же пирамида Мефферта, «Молдавская пирамидка» или «Японский тетраэдр». После многочисленных самостоятельных попыток раскрасить стороны пирамиды в однотонные цвета загадка, как собирать треугольный кубик Рубика, многим не дает покоя. Настало время разгадать эту головоломку.

Немного истории

Те, кто впервые видит пирамиду Мефферта, ошибочно предполагают, что ее изобрели, основываясь на схеме кубика Рубика. Но это не так. Пирамида Мефферта появилась на 3 года раньше, чем привычная всем кубическая головоломка. Ее изобрел немецкий предприимчивый молодой человек Уве Мефферт.

Изначально он сделал эту игрушку для собственного развлечения, используя несколько кусочков дерева, резинку и центральный шар. Ему даже и в голову не пришло, что эта головоломка может быть еще кому-то интересной. Но все изменилось, когда в 1975 году Эрне Рубик запатентовал кубик Рубика и начал продвигать его в массы. Тогда Мефферт вспомнил о своей пирамиде и заставил весь мир задуматься, как собирать треугольный кубик Рубика.

Конструкция

Конструкция головоломки играет ключевую роль в ее разгадке. Поэтому прежде чем узнать, как собирать треугольный кубик Рубика, нужно понять, что он собой представляет.

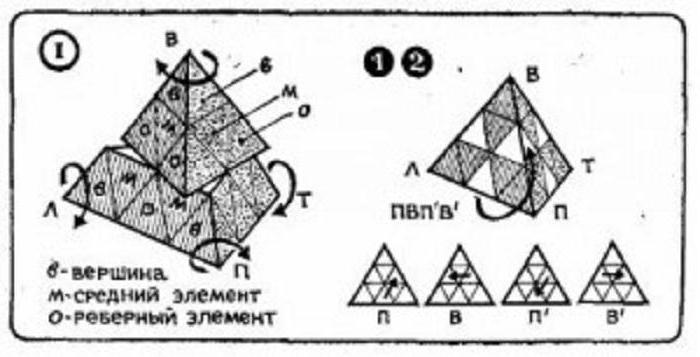
Пирамида Мефферта состоит из:

• 4-х осевых элементов;
• 6-и реберных элементов;
• 4-х тривиальных угловых.

Каждый осевой элемент, в свою очередь, имеет треугольники, обращенные на три смежные грани. Пирамида Мефферта сконструирована таким образом, что каждый ее фрагмент при вращении может спокойно перемещаться и не выпадать из нее.

Если говорить о том, как собирать треугольный кубик Рубика, то следует отметить, что при такой конструкции головоломки возможно 75 582 720 конфигураций. Эта цифра не такая пугающая, если учесть во внимание, что конструкция классического кубика Рубика предполагает 43 252 003 489 856 000 возможных состояний.

Модификации

Кроме пирамидки Мефферта и кубика Рубика, есть еще одна схожая головоломка – тетраминкс. Формой усеченного тетраэдра она визуально напоминает «Молдавскую пирамидку». Но, несмотря на схожесть, имеет абсолютно другой механизм.

Люди, понимающие, как собрать кубик Рубика 3х3, схема сборки которого сегодня доступна каждому, с легкостью разберутся и с тетраминксом. Потому что в отличие от пирамиды Мефферта, в тетраминксе нужно не только упорядочить цвета по его сторонам, но и восстановить сам тетраэдр.

Алгоритм Бога

Алгоритм Бога – это продуманный алгоритм решения головоломки, при котором нужно совершить минимальное количество действий. Это относится ко всем головоломкам, которые имеют конечное число конфигураций и ходов. К таковым можно отнести: пирамиду Мефферта, Ханойскую башню, Такен.

Как собрать кубик Рубика? Схемы для начинающих основываются на алгоритме Бога, подразумевающем нахождение оптимального решения головоломки для возвращения начальной конфигурации пирамиды в конечную.

Число Бога

Из определения алгоритма Бога следует еще одно понятие – «число Бога». Это максимальное количество ходов, за которое можно решить головоломку при самой сложной начальной конфигурации. То есть это такое число, за которое пирамида Мефферта и другие аналогичные головоломки всегда могут быть разгаданы. Если количество ходов превысило данное число, то при решении был нарушен алгоритм Бога.

Если говорить о том, как собрать кубик Рубика 3х3, то схема сборки, составленная математически верно, не может превышать 20 действий. Для пирамиды Мефферта максимальное количество ходов, за которое она может быть разгадана – 11.

Как собрать треугольный кубик Рубика? Способ 1

Разобравшись в строении и основных терминах, применяемых при сборке «Монгольской пирамидки», можно приступать непосредственно к самому процессу. Собрать тетраэдр гораздо легче, чем куб. Поэтому начинать знакомиться с подобными головоломками лучше с него.

• Внимательно рассмотреть все грани пирамиды и развернуть ее вершины так, чтобы они совпадали с цветом среднего элемента.
• На одной из сторон развернуть средние тетраэдры так, чтобы три вершины с соприкасающимися к их сторонам треугольниками были одного цвета. Чтобы понять, на какой из сторон начать складывать пирамиду, следует взглянуть на вершину противоположной грани. Сторона конечной конфигурации пирамиды будет того цвета, которого на ней нет.
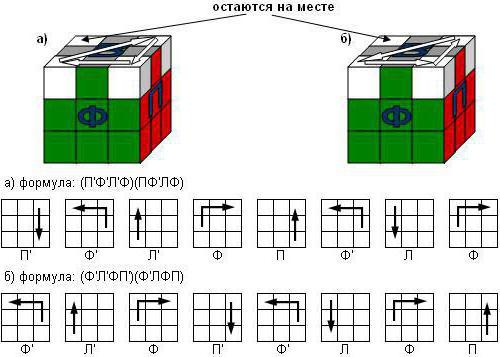
• Построить основание пирамиды. Для этого нужно выделить нижний центральный треугольник, имеющий одинаковый цвет со строящейся гранью. Затем провернуть ось, на которой он находится, вправо. Горизонтальный ряд под вершиной пирамиды – влево. Рабочую ось вернуть в исходное положение. Горизонтальный ряд нужно провернуть вправо.

• Чтобы выстроить нижний ряд, требуется посмотреть на полученный результат. Если треугольник нужного цвета находится на строящейся грани, следует три диагональных элемента на нижней левой вершине провернуть влево. Горизонтальный ряд под центральной вершиной – влево. Повторить первое действие в обратном направлении. Если нужного цвета нет на строящейся грани, тогда центральная часть пирамиды проворачивается против часовой стрелки. Горизонтальный ряд под центральной вершиной – вправо. И снова первое действие повторяется, только уже по часовой стрелке.
• Провернуть вершину до полной сборки граней и перевернуть пирамидку вниз.

Таким же образом собираются все остальные стороны тетраэдра. Это самая простая и распространенная схема, как собрать треугольный кубик Рубика. Если при правильной последовательности действий головоломка так и остается неразгаданной, нужно проверить конструкцию пирамидки. Возможно, она была нарушена при производстве.

Способ 2

Второй способ предназначен для скоростной сборки пирамиды Мефферта. Послойное построение позволяет справиться с задачей всего за 30 секунд. Но основание выстраивается точно так же, как и в первом способе. Далее процесс зависит от получившейся конфигурации.

Если 2 реберных элемента расположены на своих местах в развернутом положении, то:

1. Три диагональных элемента на нижней правой вершине провернуть вниз.
2. Три диагональных элемента на нижней левой вершине – вниз.
3. В такой же последовательности совершить эти действия в обратном направлении.

Если 3 треугольника при вершине расположены не на своих местах, но при повороте на 120 градусов становятся правильно, нарушая положение вершины и центрального элемента:

1. Когда нужные треугольники находятся на правой грани от исходной, три диагональных элемента на нижней правой вершине нужно провернуть вниз.
2. Горизонтальный ряд под центральной вершиной – вправо.
3. Повторить первое действие в обратном направлении.
4. Горизонтальный ряд под центральной вершиной снова провернуть вправо.
5. Три диагональных элемента на нижней правой вершине – вниз.
6. Горизонтальный ряд под центральной вершиной – вправо.
7. Три диагональных элемента на нижней правой вершине – вверх.

Когда нужные элементы находятся на левой грани, действия аналогичны, только их нужно проделывать в обратном направлении.

Как легко собрать кубик Рубика 3х3? Схемы для детей позволяют быстро наловчиться в столь увлекательном процессе, но начинать тренировки следует все-таки с пирамиды. Благодаря конструкции ее можно собрать всего за 11 ходов при всех возможных конфигурациях. Поэтому желаемого результата можно добиться гораздо быстрее, что вдохновит на решение более сложных головоломок.

Источник

Треугольник объемный название

Названия геометрических фигур в картинках (23 ФОТО)

Геометрия как наука началась с древних греков. Они подстмотрели у египтян землемерные работы и оформили это в виде аксиом и правил. Первым научным трудом в этой области был «Начала» Евклида.

Объёмные геометрические фигуры

Названия объёмных фигур на английском

Синие фигуры с английскими названиями

Синие фигуры с русскими названиями

Разноцветные фигуры с английскими названиями

Простые фигуры кубической сингонии

Куб, икосаэдр, тетраэдр, октаэдр, додекаэдр

Весёлые геометрические фигуры

Треугольник, пятиугольник, шестиугольник, семиугольник, восьмиугольник

Какие бывают геометрические фигуры?

Какие бывают геометрические фигуры?

В сферу изучения науки геометрии входят плоские (двухмерные) фигуры и объмные фигуры (трхмерные).

Их изучает планиметрия. Точка тоже плоская фигура.

Двухмерные фигуры — треугольник, квадрат, прямоугольник, ромб, трапеция, параллелограмм, круг, овал, эллипс, многоугольники (пентагон, гексагон, гептагон, октагон и другие).

К фигурам также относится и точка.

Трехмерные фигуры — куб, сфера, полусфера, конус, цилиндр, пирамида, параллелепипед, призма, эллипсоид, купол, тетраэдры и множество других, выходящие из вышеуказанных. Далее идут очень сложные геометрические фигуры — различные многогранники, которые по сути могут содержать бесконечное количество граней. Например, большая клинокорона — состоит из 2-х квадратов и 16-ти правильных треугольников или клинокорона, составленная из 14 граней: 2 квадрата и 12 правильных треугольника.

Говоря о геометрических фигурах, можно выделить такие две закономерные группы как:

Итак, поподробнее о двухмерным, к ним можно отнести такие фигуры как:

А вот что касается трхмерных фигур, то вот какими они могут быть:

Очертания фигур и все возможные действия с ними изучают математические науки геометрия (изучает плоские фигуры) и стереометрия (предмет изучения — объемные фигуры). Я в школе любила и ту, и другую науку.

Вот так классифицируются плоские (2D) фигуры:

С тремя сторонами — это треугольник. С четырьмя сторонами — это квадрат, ромб, прямоугольник, трапеция. А еще может быть параллелограмм и окружность (овал, круг, полукруг, эллипс).

Объемные фигуры (3D) классифицируются таким образом:

Это куб, параллелепипед, тетраэдр, цилиндр, пирамида, икосаэдр, шар, додекаэдр, конус, октаэдр, призма, сфера. К тому же есть усеченные фигуры (пирамида, конус). В зависимости от основания, пирамида, призма делятся на треугольные, четырехгранные и так далее.

Детские игрушки (пирамидки, мозаика и другие) позволяют с раннего детства знакомить детей с геометрическими объемными фигурами. А плоские фигуры можно нарисовать и вырезать из бумаги.

Из двухмерных можно назвать следующие:

• круг;
• овал;
• квадрат;
• прямоугольник;
• параллелограмм;
• трапеция;
• пятиугольник (шестиугольник и т.д.);
• ромб;
• треугольник.

С трехмерными немного посложнее:

• куб;
• цилиндр;
• конус;
• призма;
• сфера или шар;
• параллелепипед;
• пирамида;
• тетраэдр;
• икосаэдр;
• октаэдр;
• додекаэдр.

Думаю многие, прочитав последния названия, спросили про себя: quot;Что-что?quot;. Для наглядности — иллюстрация:

На самом деле фигур в математике достаточно. Плоские фигуры это — прямоугольники, квадрат, треугольник, пятиугольник, шестиугольник, круг. Объемные фигуры или 3D фигуры — это как пирамида, так и куб и додекаэдр, и тд.

круг, треугольник, квадрат, ромб, прямоугольник, трапеция, параллелограмм, овал и многоугольник. Ещ звезда (пентаграмма), если е можно называть фигурой.

Призма, пирамида, параллелепипед, призма, шар (сфера), цилиндр, полусфера (половинка от сферы, то есть шар, разрезанный пополам) и конус. Пирамиды делятся на треугольные, четырхугольные и так далее (почти до бесконечности). Чем больше у пирамиды углов в основании, тем больше она напоминает конус.

Двухмерные фигуры (2D): угол; многоугольник (разновидности многоугольников: треугольник, четырхугольник разновидности четырхугольника: параллелограмм, прямоугольник, ромб, квадрат, трапеция, дельтоид, пятиугольник, шестиугольник и т. д. до бесконечности); окружность, круг, круговой сегмент, круговой сектор, эллипс, овал.

Трхмерные фигуры (3D): двугранный угол, многогранный угол; многогранник (разновидности многогранников: призма разновидности призмы: параллелепипед, куб, антипризма, пирамида разновидность тетраэдр, усечнная пирамида, бипирамида разновидность октаэдр, додекаэдр, икосаэдр, клин, обелиск); цилиндр, усечнный цилиндр, отрезок цилиндра (он же цилиндрическая подковка или quot;копытоquot;), конус, усечнный конус, сфера, шар, шаровой сегмент, шаровой слой, шаровой сектор, эллипсоид, геоид.

С самого начала мы на уроках геометрии изучаем простые фигуры, которые являются плоскими, то есть располагаются на одной плоскости.

Далее, перед нами открывается мир объмных фигур, которые необходимо представлять и понимать, как они расположены и как грамотно их нарисовать, чтобы было понятно не только вам, но и окружающим.

Итак, перечень основных фигур можно изучить ниже.

В последнее время мне как раз приходилось рассказывать своим внучкам и внуку, какими могут быть геометрические фигуры.

Начинали с плоских фигурок, вырезанных из картона или сделанные из пластмассы, дети учились различать треугольник и квадрат, овал и круг, прямоугольник, ромб и многоугольник.

Помогали в запоминании названий фигур и вот такие специальные игрушки с отверстиями определнной формы.

Позднее перешли на объмные фигурки, кубики и конусы, параллелепипеды, шары и кольца, пирамидки и цилиндры.

До школы они пока не доросли, а когда пойдут, то их научат различать равнобедренные и равносторонние треугольники, узнают про луч и точку, про окружность и вс остальное.

треугольник в объеме — Как называется объемный треугольник. Вот квадрат — кубом, а треугольник — ? — 22 ответа

В разделе Другое на вопрос Как называется объемный треугольник. Вот квадрат — кубом, а треугольник — ? заданный автором Дарья Попкова лучший ответ это Тетраэдр.

[гуру]пирамидаОтвет от Евровидение[новичек]незнОтвет от Прострочить[новичек]хзОтвет от Обособиться[новичек]ПирамидаОтвет от Ёофья Раскопова[новичек]ПИРАМИДАААА!!

Ответ от сергей беляев[новичек]Так-то у тетраэдра 4 угла, а у пирамиды их 5. Какой и них-зависит от кол-ва углов в основанииОтвет от Денис Рыбкин[активный]Пирамида или тетраэдр. Но гораздо чаще его называют пирамидойОтвет от Артур Татулян[новичек]Разница между пирамидой и тетраэдром в том, что у пирамиды четыре боковые грани в виде треугольников и нижняя грань в виде прямоугольника, а у тетраэдра три боковые грани в виде треугольников и нижняя грань в виде треугольника. По этому грамотнее будет, если сказать, что объемный треугольник — тетраэдр, так как все грани тэтраэдра в виде треугольников!Ответ от сафонов савелий[новичек]ПирамидаОтвет от Golubev Konstantin[новичек]Треугольная ПризмаОтвет от Любовь К[новичек]тэтраздерТреугольник на ВикипедииПосмотрите статью на википедии про ТреугольникТреугольник Рёло на ВикипедииПосмотрите статью на википедии про Треугольник Рёло

Виды треугольников

В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.

Виды треугольников по углам:

• остроугольные
• прямоугольные
• тупоугольные

Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).

Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).

Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).

Виды треугольников по сторонам:

• равносторонние
• равнобедренные
• разносторонние

Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.

Отрезки равной длины на чертеже отмечают равным количеством черточек:

Источник