Abcda1b1c1d1 куб найдите угол между прямыми содержащими отрезки

Нахождение угла между прямыми

\(\blacktriangleright\) Угол между прямыми – это такой угол \(\alpha\) , что \(0\leqslant \alpha\leqslant 90^\circ\) .

\(\blacktriangleright\) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.

\(\blacktriangleright\) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.

Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.

\(\blacktriangleright\) Порядок нахождения угла между скрещивающимися прямыми:

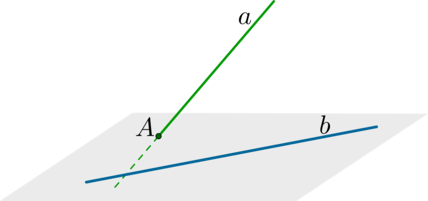
Шаг 1: через одну из двух прямых \(a\) провести плоскость, параллельную второй прямой \(b\) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);

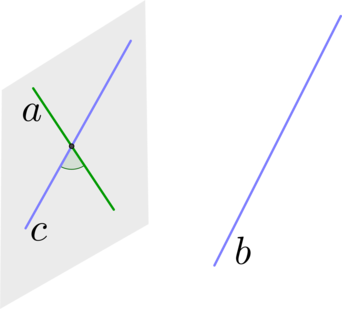
Шаг 2: в этой плоскости найти прямую \(c\) , параллельную прямой \(b\) ;

Шаг 3: тогда угол между прямыми \(a\) и \(b\) будет равен углу между прямыми \(a\) и \(c\) .

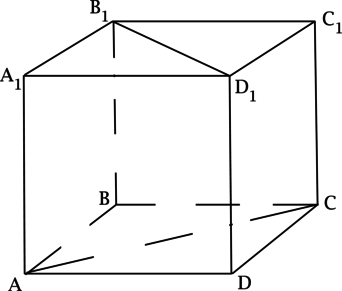
\(ABCDA_1B_1C_1D_1\) – куб. Найдите угол между прямыми, содержащими отрезки \(AC\) и \(B_1D_1\) . Ответ дайте в градусах.

Прямая \(BD\) параллельна прямой \(B_1D_1\) , тогда угол между \(AC\) и \(B_1D_1\) равен углу между \(AC\) и \(BD\) , но \(AC\) и \(BD\) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ \(90^<\circ>\) .

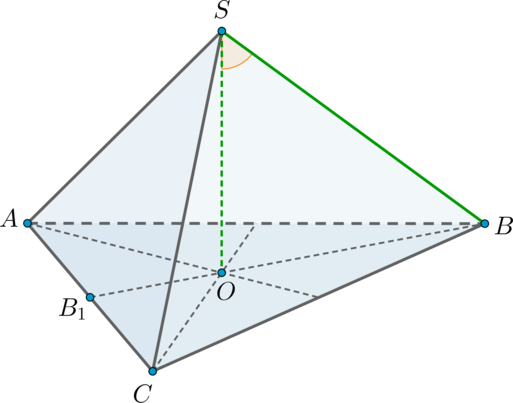
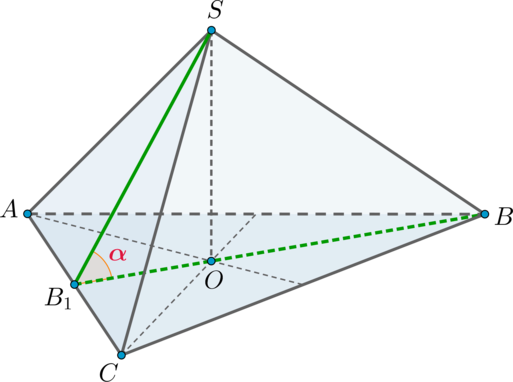
Дана правильная треугольная пирамида \(SABC\) с вершиной \(S\) . Найдите угол между высотой пирамиды и ребром \(SB\) , если высота пирамиды равна \(2\sqrt3\) , а сторона основания пирамиды равна \(6\) . Ответ дайте в градусах.

Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота \(SO\) падает в точку пересечения медиан основания.

Пусть \(BB_1\) – медиана, а значит, и высота. По теореме Пифагора \[BB_1=\sqrt=3\sqrt3 \quad\Rightarrow\quad BO=\dfrac23BB_1=2\sqrt3,\] так как медианы точкой пересечения делятся в отношении \(2:1\) , считая от вершины.
Следовательно, прямоугольный \(\triangle SOB\) является равнобедренным ( \(SO=BO=2\sqrt3\) ), значит, острые углы равны по \(45^\circ\) .

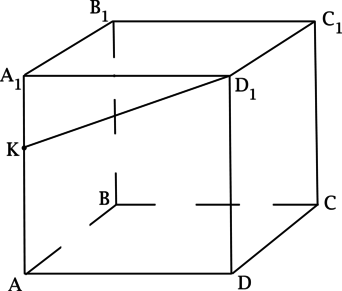
\(ABCDA_1B_1C_1D_1\) – куб. Точка \(K\) лежит на ребре \(AA_1\) . Найдите угол между прямыми, содержащими отрезки \(D_1K\) и \(AB\) . Ответ дайте в градусах.

Так как \(ABCDA_1B_1C_1D_1\) – куб, то \(AB\) перпендикулярен плоскости \((ADD_1)\) , тогда \(AB\) перпендикулярен любой прямой, лежащей в плоскости \((ADD_1)\) , следовательно, угол между прямыми, содержащими отрезки \(D_1K\) и \(AB\) равен \(90^<\circ>\) .

Дан правильный тетраэдр \(SABC\) . Найдите квадрат тангенса угла между высотой грани \(SAC\) , опущенной из вершины \(S\) , и высотой грани \(ABC\) , опущенной из вершины \(B\) .

Пусть \(SB_1\) – высота грани \(SAC\) . Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть \(SB_1\) также является и медианой, значит, \(AB_1=B_1C\) . Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если \(SO\) – высота, то \(O\) – точка пересечения медиан треугольника \(ABC\) , а значит и высот, так как \(\triangle ABC\) правильный. Следовательно, \(BB_1\) — медиана и высота.

Таким образом, необходимо найти \(\mathrm^2\angle (SB_1, BB_1)\) .
Пусть \(a\) – ребро тетраэдра. Тогда \(BC=a, B_1C=0,5a\) , следовательно, по теореме Пифагора \[BB_1=\sqrt=\dfrac<\sqrt3>2a\] Так как \(O\) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении \(2:1\) , считая от вершины, то \(OB_1=\frac13BB_1=\frac<\sqrt3>6a\) .

Так как \(\triangle ABC=\triangle SAC\) , то \(SB_1=BB_1\) . Следовательно, из прямоугольного \(\triangle SB_1O\) : \[\cos \alpha=\dfrac=\dfrac13 \quad\Rightarrow\quad \sin \alpha =\sqrt<1-\cos^2\alpha>=\dfrac<2\sqrt2>3 \quad\Rightarrow\quad \mathrm^2\alpha=(2\sqrt2)^2=8.\]

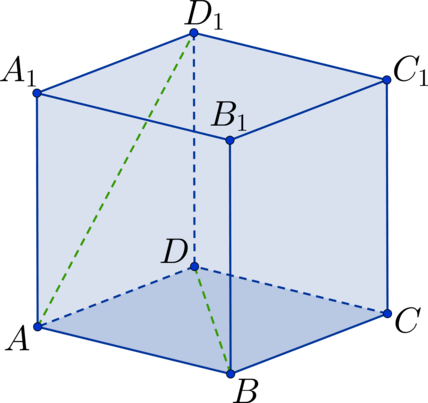
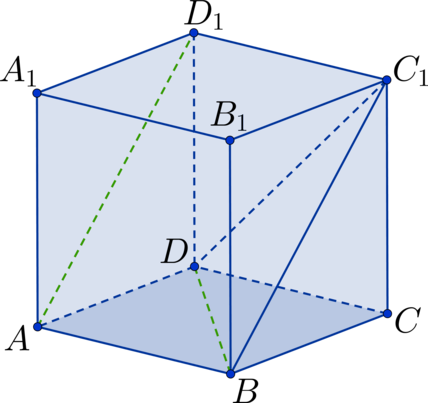
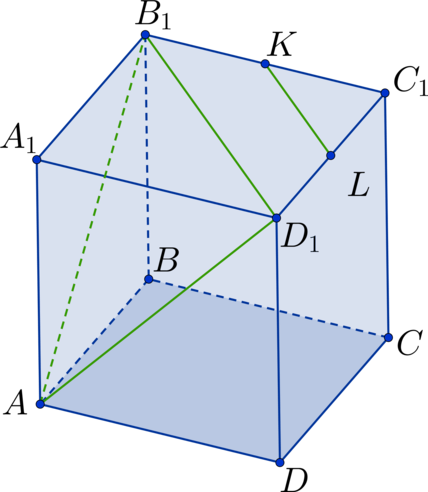
Дан куб \(ABCDA_1B_1C_1D_1\) . Найдите угол между прямыми \(AD_1\) и \(BD\) . Ответ дайте в градусах.

Заметим, что \(BC_1 || AD_1\) , тогда рассмотрим треугольник \(\triangle BDC_1\) , в котором необходимо определить \(\angle DBC_1\) . Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали \(\Rightarrow\) \(\triangle BDC_1\) – равносторонний треугольник \(\Rightarrow\) \(\angle DBC_1 = 60^\circ\) .

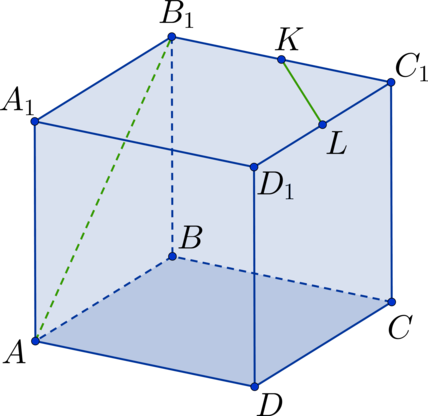
Дан куб \(ABCDA_1B_1C_1D_1\) . Точка \(K\) – середина стороны \(B_1C_1\) , а точка \(L\) – середина стороны \(C_1D_1\) . Найдите угол между прямыми \(AB_1\) и \(KL\) . Ответ дайте в градусах.

Проведем диагональ \(B_1D_1\) в квадрате \(A_1B_1C_1D_1\) . Тогда \(KL\) – средняя линия в \(\triangle B_1C_1D_1\) \(\Rightarrow\) \(KL || B_1D_1\) \(\Rightarrow\) \(\angle AB_1D_1\) – искомый угол. Рассмотрим \(\triangle AB_1D_1\) . Он состоит из диагоналей соответствующих квадратов \(\Rightarrow\) треугольник является равносторонним \(\Rightarrow\) \(\angle AB_1D_1 = 60^\circ\) .

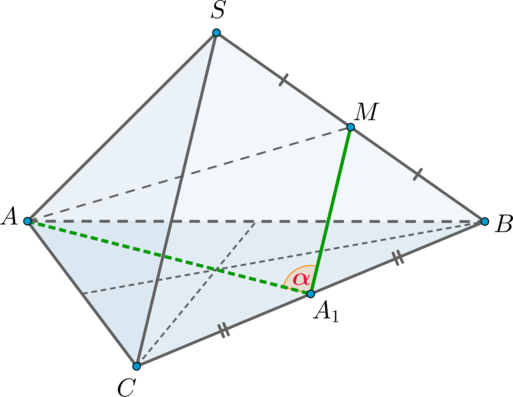
Дана правильная треугольная пирамида \(SABC\) с вершиной \(S\) . Найдите косинус угла между высотой основания \(AA_1\) и ребром \(SC\) , если сторона основания равна \(\sqrt3\) , а боковое ребро равно \(2\) .

Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, \(AA_1\) также является и медианой.

Заметим, что прямые \(AA_1\) и \(SC\) скрещиваются. Проведем \(A_1M\parallel SC\) , следовательно, \(\angle (AA_1, SC)=\angle (AA_1, A_1M)\) .
Так как \(A_1M\parallel SC\) и \(A_1\) – середина \(BC\) , то \(M\) – середина \(SB\) . Следовательно, \(A_1M\) – средняя линия и \[A_1M=\frac12SC=1.\] По теореме Пифагора из \(\triangle ABA_1\) : \[AA_1=\sqrt=\dfrac32.\] Медиану \(AM\) из \(\triangle SAB\) можно найти по формуле медианы: \[AM^2=\dfrac<2AS^2+2AB^2-SB^2>4=\dfrac52.\] Следовательно, по теореме косинусов из \(\triangle AA_1M\) : \[\cos \alpha=\dfrac<2AA_1\cdot A_1M>=\dfrac14=0,25.\]

Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.

Основные моменты

В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.

Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.

Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».

Источник

Задачи с ЕГЭ. Куб. Угол между прямыми.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

(1;1;0)
В кубе ABCDA1B1C1D1 точки E и K середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
y
z
x
D1
B
A
D
C
B1
C1
A1
E
K
(1;0;0)
Найдем координаты точек A, Е, В, K.
AE
1.
BK
2.
(0; ; 1)
2
1
(- ; 0; 1)
2
1
1
1
1
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому можно взять ребро куба, например, a или х. А можно рассмотреть единичный куб, все ребра которого равны 1.

(1; ;1)
2
1
( ;1;1)
2
1
Найдем координаты

векторов АЕ и ВК.
?
?
?
?
Чтобы найти координаты вектора вычтем из координат конца вектора соответствующие координаты начала вектора.


Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.
D
А
В
С
А1
D1
С1
В1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Куб отлично вписывается в систему координат.
К
1
2
1
2
х
y
z
?
(1;0; )
1
2
?
(1;1;0)
?
(0;1;0)
?
(1;0;1)
1
1
1
1
2 способ
1 способ

Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.
D
А
В
С
А1
D1
С1
В1
1
1
1
2
К
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Заменим BA1 на параллельную прямую CD1. Угол между прямыми А1В и СК будет равен углу между CD1 и СК.
a
1
2
1
2
1
5
2
5
2
2 способ

Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.
D
А
В
С
А1
D1
С1
В1
1
1
1
2
К
a
1
2
1
2
1
5
2
5
2
3
2
Применим теорему косинусов для треугольника CKD1. Я хочу найти косинус угла KCD1, значит, составляем теорему косинусов для стороны KD1:

A
D
C
A1
B1
C1
D1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Куб отлично вписывается в систему координат.
х
y
z
?
?
(0;0;1)
?
(0;1;0)
?
(0;1;1)
1
1
1
1 способ
Точка M – середина ребра АD куба АВСDA1B1C1D1. Найдите угол между прямыми C1M и B1С.

1
1
A
D
C
A1
B1
C1
D1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Рассмотрев это трудоёмкое решение, метод координат показался мне «конфеткой».
2 способ
Точка M – середина ребра АD куба АВСDA1B1C1D1. Найдите угол между прямыми C1M и B1С.

M
1
2
1
2
a
1
1
1
2
2
1
2
1
13
2
3
2
Применим теорему Пифагора к трем треугольникам.
К
К1
L
L1
Закончи решение самостоятельно.
Ответ:
Составим теорему косинусов для стороны MK.

B
A
D
B1
C1
D1
A1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Куб отлично вписывается в систему координат.
х
y
z
?
?
(0;0;1)
?
1
1
1
1 способ
C
(0;1; )
1
2
(1;1;0)
Точка Е – середина ребра DD1 куба ABCDA1B1C1D1 найдите угол между прямыми СЕ и АС1.
E

B
A
D
B1
C1
D1
A1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Куб отлично вписывается в систему координат.
х
y
z
?
?
(0;0;1)
?
1
1
1
1 способ
C
(1;0;0)
(0;0; )
1
3
(1;1;0)
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что
СЕ : ЕС1 = 1 : 2. Найдите угол между прямыми ВЕ и АС1.
E

B
A
B1
C1
D1
A1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
1
1
1
C
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что
СЕ : ЕС1 = 1 : 2.
Найдите угол между прямыми
ВЕ и АС1.
E
1
3
2
3
K
3
13
3
D
a
10
3
Чтобы найти угол составим теорему косинусов для стороны KC1 в AKC1.
3
12
4
2 способ

Точка Е – середина ребра DD1 куба ABCDA1B1C1D1 найдите угол между прямыми СЕ и АС1.
C
A
D1
C1
B
B1
1
D
A1
1
E
2
K
K1
N
N1
L
1
1
2
1
2
3
2
5
1
5
21
2
a
Чтобы найти угол составим теорему косинусов для стороны KL в KLD1.
Отрицательное значение косинуса говорит о том, что угол KD1L тупой. Но в стереометрии угол между прямыми не может быть тупым. Поэтому нам нужен смежный острый угол с углом KD1L. Строить его на чертеже не обязательно.
Если косинус тупого угла – ,

то косинус смежного с ним

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 595 961 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Добавить в избранное

• 19.04.2021 558
• PPTX 461.9 кбайт
• 3 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Исмоилов Сарвар Шодиевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Каждый второй ребенок в школе подвергался психической агрессии

Университет им. Герцена и РАО создадут портрет современного школьника

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Школьник из Сочи выиграл международный турнир по шахматам в Сербии

Минпросвещения России подготовит учителей для обучения детей из Донбасса

Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник